Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Resonance
Unlock Audio Lesson
Today we're diving into a special case in differential equations—resonance. Can anyone tell me what happens during resonance in a physical system?
Isn't it when the forcing function matches the system’s natural frequency?
Exactly! When that happens, the system can respond with significantly amplified motion. For example, if we have a system defined by the equation \(\dfrac{d^2y}{dx^2} + \omega^2 y = \cos(\omega x)\), the term \(\cos(\omega x)\) is our forcing function.
So, if \(\cos(\omega x)\) is included, does it affect the way we find the particular integral?
Great question! Normally we might guess a particular integral as \(A \cos(\omega x) + B \sin(\omega x)\). However, because it already appears in the complementary function, we must modify our guess.
Solution Approach to Resonance
Unlock Audio Lesson
Let's talk about how to adjust our guess for the particular integral when resonance occurs. Can anyone think of what modification we should make?
Maybe we multiply by x to make it independent of the complementary function?
Yes! That's correct. So, we modify our guess to \(y_p = x(A \cos(\omega x) + B \sin(\omega x))\). This change reflects that the response grows with x.
What does this mean practically for a structure?
It means we have to be cautious about resonance in structural design, as it can lead to excessive vibrations and potentially structural failure if not properly managed.
Significance of Resonance
Unlock Audio Lesson
Now that we understand how to find solutions related to resonance, let's explore its practical implications. Why do we care about avoiding resonance in engineering?
Because it can lead to dangerous oscillations in structures, right?
Exactly! For engineers, particularly in civil and mechanical fields, controlling resonance is critical for safety. Remember, systems that resonate can amplify vibrations to dangerous levels.
Could you give an example of where this matters?
Sure! Consider bridges and tall buildings. They need to be designed to withstand forces from wind and seismic activity, which could cause resonance.
Recap of Key Points
Unlock Audio Lesson
To wrap up our discussion, can someone summarize what we've learned about resonance?
We learned that resonance occurs when the forcing frequency matches the natural frequency and that we must adjust our particular integral guess to account for this.
Great summary! And what did we discover about the implications of resonance in design?
We found that resonance can amplify responses, which is critical for structural integrity and safety.
Excellent! Remember to always consider resonance when analyzing and designing systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section focuses on the phenomenon of resonance in differential equations, highlighting how a forcing function like cos(ωx) can match the natural frequency of the system. It discusses how to modify the guess for the particular integral when resonance occurs by multiplying by x, leading to a growing response in the system that is critical in structural dynamics.
Detailed
Special Case: Resonance
In mechanical and structural systems, resonance is a critical phenomenon that occurs when the frequency of an external forcing function matches the natural frequency of the system. The classic example given is the second-order differential equation:
$$\frac{d^2y}{dx^2} + \omega^2 y = \cos(\omega x)$$
Here, the term cos(ωx) acts as the forcing function that matches the natural frequency.
Solution Approach
- The complementary function is calculated as:
$$y_h = C_1 \cos(\omega x) + C_2 \sin(\omega x)$$
However, since cos(ωx) appears in the complementary function, the method of guessing the particular integral as Acos(ωx) + Bsin(ωx) fails. - To adapt to this, a modification rule states that you should multiply the guess by x:
$$y_p = x(A\cos(\omega x) + B\sin(\omega x))$$
This adjustment reflects the resonant behavior, showing that the response grows with increasing x, indicating an amplification crucial for understanding dynamics in structures. This amplification highlights the importance of considering resonance in engineering applications and the design of mechanical systems.
Youtube Videos
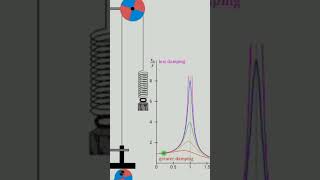
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Resonance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In mechanical and structural systems, resonance occurs when the frequency of the forcing function matches the natural frequency of the system.
Detailed Explanation
Resonance is a phenomenon that occurs in systems such as buildings, bridges, and mechanical structures when an external force is applied at a frequency that is equal to the system's natural frequency. This can lead to significant vibrations and can amplify responses in the structure, sometimes to detrimental levels. The idea is that every physical structure has a frequency at which it tends to oscillate, and if an external force is applied at that same frequency, it can cause the structure to respond strongly.
Examples & Analogies
A good analogy for this is pushing a swing. If you push a swing at the right timing (its natural frequency), the swing will go higher and higher, reflecting how resonance can build up energy in systems.
Example of Resonance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider:
d²y/dx² + ω²y = cos(ωx)
Here, the forcing function cos(ωx) matches the natural frequency of the system.
Detailed Explanation
In this example, the given differential equation models a system subjected to a periodic force represented by cos(ωx). The term ω² signifies the natural frequency of the system. When the forcing function's frequency (cos(ωx)) aligns perfectly with the system's natural frequency (ω), the resultant motion can increase dramatically — a hallmark of resonance.
Examples & Analogies
Think of a musical instrument, like a guitar. If you pluck a string at just the right frequency, the string will vibrate powerfully, creating a loud sound. This is similar to how a resonant system responds to forces at its natural frequency.
Solution Approach for Resonant Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• CF: y = C cos(ωx) + C sin(ωx)
• Since cos(ωx) appears in the CF, guessing PI as Acos(ωx) + Bsin(ωx) fails.
Modification Rule: Multiply the guess by x → Try:
y = x(Acos(ωx) + Bsin(ωx))
Detailed Explanation
When solving the resonant case, we first find the complementary function (CF), which is the solution to the homogeneous part of the equation. However, since the forcing function (cos(ωx)) already appears in the CF, simply guessing a particular integral (PI) of the same form won't work. Instead, we apply a modification rule — we multiply our guess by x (making it x(Acos(ωx) + Bsin(ωx))) to ensure it is a linearly independent solution. This adjustment allows us to capture the resonance phenomenon accurately, where the system's response is amplified.
Examples & Analogies
Imagine a famous bridge that starts swaying when the wind hits it just right. If engineers mistakenly used the same calculations that predicted small movements without acknowledging the increasing sway (equivalent to multiplying our guess by x), they could miss predicting a possible structural failure. Adjusting our calculations to include the extra sway is similar to adding that 'x' factor in our mathematical treatment of the resonance.
Implications of Resonance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This reflects resonant behavior where the response grows with x, showing amplification — a critical concept in structural dynamics.
Detailed Explanation
The amplification effect of resonance is critical to understand in engineering. As the response grows with 'x' in the modified guess, we recognize that tiny oscillations can lead to large responses over time, which can not only be dangerous but also catastrophic if unaccounted for. This is why engineers must design structures that can withstand or avoid resonance with their natural frequencies.
Examples & Analogies
Consider the scenario of a child on a playground swing — if the child continues to push at the right moment, the swing goes higher and higher. Similarly, in engineering, if a building resonates with wind forces, it may experience dangerous swaying or even failure, much like the swing reaching a height where it could fall off unexpectedly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Resonance: When an external frequency matches natural frequency, leading to amplified responses.
-
Complementary Function: The solution to the homogeneous part of the differential equation.
-
Modification Rule: Adjustment in methods to account for the presence of resonance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of resonance in a bridge where traffic frequency matches the natural frequency, potentially leading to structural failure.
-
The tuning of musical instruments where the frequency of different components creates resonant effects.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Resonance can amplify, making structures sway, keep frequencies apart to keep danger at bay.
📖 Fascinating Stories
-
Picture a bridge that dances with traffic; if cars rush in rhythm with its natural beat, a disaster could unfold! Engineers must adjust the bridge's design to prevent such a fate.
🧠 Other Memory Gems
-
Remember the word 'AMP' for resonance: A - Amplitude grows, M - Matches frequency, P - Particularly modified.
🎯 Super Acronyms
R.A.M.P. for Resonance
- R: - Resonance
- A: - Amplification
- M: - Modification Rule
- P: - Particularly affected systems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Resonance
Definition:
A phenomenon that occurs when the frequency of an external forcing function matches the natural frequency of a system, potentially leading to increased amplitude of oscillation.
-
Term: Complementary Function
Definition:
The general solution of the associated homogeneous differential equation.
-
Term: Particular Integral
Definition:
A specific solution to a non-homogeneous differential equation.
-
Term: Forcing Function
Definition:
An external input or disturbance applied to a system, represented mathematically in differential equations.