Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Basics of Arbitrary Constants
Unlock Audio Lesson
Today, we're discussing how we can form Partial Differential Equations by eliminating arbitrary constants. Can anyone explain what we mean by 'arbitrary constants'?
Are they constants that can take any value?
Exactly! They are not fixed and can vary. For example, in the relation `z = ax + by + ab`, `a` and `b` are arbitrary constants. Now, why do you think we need to eliminate them?
To simplify the equation and find the relationship between `z`, `x`, and `y`?
Precisely! By eliminating these constants, we focus on how `z` changes with respect to `x` and `y`. Let's explore how we do that next.
Differentiation of Relations
Unlock Audio Lesson
Now, let’s differentiate the function we mentioned, `z = ax + by + ab`. Who can tell me how to find `∂z/∂x`?
It would be `a`.
Great! And what about `∂z/∂y`?
`b`.
Exactly! Now, if we have both derivatives, how can we eliminate `a` and `b` to form a PDE?
By substituting them back into the equation?
Yes! Once we have the expressions for `a` and `b`, we can substitute them back to eliminate them and derive our PDE. Let’s summarize this step.
Formulating the PDE
Unlock Audio Lesson
After differentiating, how can we present our findings as a PDE?
We can write it as a relationship that doesn’t involve those constants, right?
"Yes! So for `z = ax + by + ab`, we can express the PDE as
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section details the method of forming PDEs by differentiating a function involving arbitrary constants and then eliminating these constants to yield a PDE. It emphasizes the importance of partial differentiation in this process.
Detailed
Detailed Summary
This section explores how Partial Differential Equations (PDEs) can be derived from given relations by removing arbitrary constants. Let's consider a function involving constants and independent variables, such as:
Example Relation
For a relation like z = ax + by + ab, we identify constants a and b as part of the function formulation.
Step-by-Step Formation
To derive a PDE:
1. Differentiate with respect to x and y:
-
\[ \frac{\partial z}{\partial x} = a \]
\[ \frac{\partial z}{\partial y} = b \]
2. By eliminating the constants a and b from these derivatives, we obtain a PDE that describes the relationship of the function z with respect to x and y.
Understanding this concept is crucial as it lays the groundwork for more complex applications of PDEs in engineering and physics. This method shows how mathematical modeling can start from broader relations and focus on the specifics by limiting arbitrary aspects.
Youtube Videos
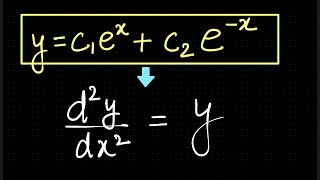
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Elimination of Constants
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let the relation involve constants a,b: Example: z = ax + by + ab.
Detailed Explanation
In this section, we begin with a relation that includes arbitrary constants, specifically 'a' and 'b'. For instance, consider the equation z = ax + by + ab. Here, 'z' is expressed in terms of 'x', 'y', and the constants 'a' and 'b'. Next, we will differentiate this equation partially to explore how to eliminate these constants.
Examples & Analogies
Think of this step like having a recipe where certain ingredients (like 'a' and 'b') are unknown. By analyzing the recipe (the equation), we can figure out the necessary adjustments to remove these unknowns, leading us to a final dish (the PDE) that's just based on the other variables.
Differentiating the Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Differentiate partially:
• ∂z/∂x = a
• ∂z/∂y = b.
Detailed Explanation
After establishing the relationship, we take partial derivatives of z with respect to x and y. This gives us two equations: ∂z/∂x = a and ∂z/∂y = b. These derivatives express how ‘z’ changes with small changes in ‘x’ and ‘y’, respectively, while keeping other variables constant. The derivatives essentially help us isolate constants 'a' and 'b'.
Examples & Analogies
Consider a company where you have different departments (x and y) producing products. By analyzing how much each department contributes (the derivatives), you can outline how important each one is to the overall output (z) without needing to worry about the individual contributions of each unknown factor (a and b).
Eliminating the Constants
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Eliminate a, b to get a PDE.
Detailed Explanation
The next step involves eliminating the constants 'a' and 'b' from our differentiated equations. By rearranging the derivatives, we form a new equation that does not rely on these constants, leading us to a Partial Differential Equation (PDE). This process highlights how specific relationships can articulate the interaction between variables without the need for previously defined constants.
Examples & Analogies
Imagine a detective solving a case. They collect evidence (the partial derivatives) to eliminate the suspects (the constants a and b), honing in on the true nature of the case (the PDE). By removing the extraneous details, they can focus on the real relationships and interactions that matter.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Arbitrary Constants: Variables in an equation that can take any value.
-
Differentiation: The process of finding the rate of change of a function.
-
PDE Formation: The method of eliminating constants through partial differentiation to form a PDE.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Given the relation z = ax + by + ab, differentiate with respect to x to find a = ∂z/∂x.
-
Utilize the derivatives ∂z/∂x and ∂z/∂y to eliminate a and b, resulting in a PDE.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In math, constants can roam, / Eliminate to find your home!
📖 Fascinating Stories
-
Imagine a scientist with a complex recipe leading to discovery. To focus on key elements, they remove unnecessary variables. This leads to cleaner results!
🧠 Other Memory Gems
-
D.E.E.P: Differentiate, Eliminate, Express as PDE.
🎯 Super Acronyms
P.O.W.E.R
- Partial derivatives
- Obtain variables
- Write relations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Partial Differential Equation (PDE)
Definition:
An equation that involves partial derivatives of a function with respect to multiple independent variables.
-
Term: Arbitrary Constants
Definition:
Constants that can take any value and are not fixed in the context of the equation.
-
Term: Differentiation
Definition:
The process of finding the derivative of a function, representing its rate of change.