Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Second-Order PDE Form
Unlock Audio Lesson
Today, we're diving into second-order partial differential equations, focusing on their classifications. These equations take the form: A∂²u/∂x² + B∂²u/∂x∂y + C∂²u/∂y² + lower terms = 0. Does anyone remember what the letters A, B, and C represent?
They are coefficients assigned to the different derivatives in the equation!
Exactly! Now, the discriminant D = B² - 4AC is crucial for classifying these PDEs. What do you think this classification does?
It helps to determine the type of physical phenomenon the PDE describes, right?
Precisely! Let’s explore how each classification—elliptic, parabolic, and hyperbolic—corresponds to different physical situations.
Discriminant and Its Importance
Unlock Audio Lesson
Let's talk about the discriminant D. What happens to the classification when D is less than zero?
It indicates the equation is elliptic, like the Laplace Equation!
Right! And what about when D equals zero?
That would make it parabolic, like the Heat Equation.
Correct! Finally, what about if D is greater than zero?
Then it’s hyperbolic, like the Wave Equation!
Good job, everyone! The physical interpretation of these classifications is vital in engineering applications.
Applications of Classification
Unlock Audio Lesson
Why do you think it's important to distinguish between elliptical, parabolic, and hyperbolic PDEs in practical applications?
It helps determine how to solve them, considering their unique characteristics!
Exactly! Each type has distinct solutions reflecting different physical behaviors. Can anyone give me an example of a real-world process for each type?
For elliptic, it's steady-state heat flow. For parabolic, it's transient heat conduction, and for hyperbolic, the propagation of waves!
Fantastic! Recognizing these differences allows engineers to select appropriate methods for solving PDEs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The classification of second-order PDEs involves determining their type—elliptic, parabolic, or hyperbolic—using the discriminant formula D = B² - 4AC. Each classification corresponds to different physical phenomena and solution behaviors.
Detailed
Classification of Second-Order PDEs
Second-order partial differential equations (PDEs) can be classified based on the discriminant D calculated from their standard form. A second-order PDE in two variables is typically represented as:
$$
A \frac{\partial^{2} u}{\partial x^{2}} + B \frac{\partial^{2} u}{\partial x \partial y} + C \frac{\partial^{2} u}{\partial y^{2}} + \text{lower order terms} = 0
$$
The discriminant is defined as:
$$
D = B^{2} - 4AC
$$
Based on the value of D, the classification is as follows:
- Elliptic: If D < 0 (e.g. Laplace Equation)
- Parabolic: If D = 0 (e.g. Heat Equation)
- Hyperbolic: If D > 0 (e.g. Wave Equation)
Each classification corresponds to different physical phenomena and affects the nature of their solutions significantly, making this classification critical for applied mathematics, particularly in areas such as engineering and physics.
Youtube Videos
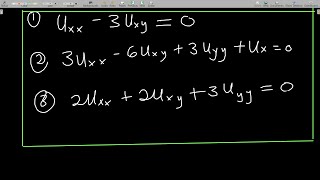
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Form of Second-Order PDEs
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A second-order PDE in two variables can be written as:
$$
\frac{\partial^2 u}{\partial x^2} A + \frac{\partial^2 u}{\partial x \partial y} B + \frac{\partial^2 u}{\partial y^2} C + \text{lower order terms} = 0
$$
Detailed Explanation
A second-order partial differential equation involves derivatives that are of second order with respect to the independent variables—in this case, x and y. It can be expressed in the form shown above, where A, B, and C are coefficients that multiply the second-order derivatives of the function u. Understanding this structure is crucial as it will help us recognize how the PDE behaves under various classifications.
Examples & Analogies
Think of a second-order PDE like a recipe that requires specific ingredients (the coefficients A, B, and C) and methods to combine them (the derivatives). Just as in cooking, where the combination of ingredients determines the taste, in PDEs, how these terms are combined defines the behavior of physical phenomena being modeled—like how heat spreads through materials.
Discriminant of the PDE
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The discriminant is given by:
$$
D = B^2 - 4AC
$$
Detailed Explanation
The discriminant D is a crucial part of understanding the classification of second-order PDEs. It is derived from the coefficients A, B, and C. The value of D reveals important information about the nature of the PDE, specifically how the solutions behave. If D is negative, the PDE is classified as elliptic; if it equals zero, it's parabolic; and if it's positive, it's hyperbolic.
Examples & Analogies
Imagine the discriminant as a traffic light for travelers. If the light is green (D > 0), there are smooth pathways—hyperbolic. If the light is yellow (D = 0), caution is advised—parabolic. If red (D < 0), it's a stop—elliptic. Each transition suggests how one should approach the situation (e.g., whether to proceed, pause or stop) just as the behavior of solutions changes based on the discriminant value.
Classification Based on D
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Classification based on D:
- Elliptic if D < 0 (e.g., Laplace Equation)
- Parabolic if D = 0 (e.g., Heat Equation)
- Hyperbolic if D > 0 (e.g., Wave Equation)
Detailed Explanation
The classification of second-order PDEs into elliptic, parabolic, and hyperbolic categories is vital because each category corresponds to different types of physical phenomena. An elliptic PDE, like Laplace's Equation, generally describes steady-state situations (like temperature distribution), parabolic PDEs, like the Heat Equation, represent time-dependent processes that evolve over time, while hyperbolic PDEs, like the Wave Equation, deal with dynamic systems where waves propagate.
Examples & Analogies
Consider these classifications as different types of weather systems. Elliptic (like calm, steady sunny days) involves stable conditions; parabolic (like a gradually warming day) signifies change over time; and hyperbolic (like thunderstorms) indicates rapid, dynamic changes. Just as understanding weather helps us prepare and respond appropriately, recognizing the type of PDE guides us in choosing the right mathematical approach to finding solutions.
Physical Phenomena Representation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These types correspond to different physical phenomena and determine the nature of their solutions.
Detailed Explanation
The classification of PDEs directly influences how they model various real-world scenarios. For example, elliptic equations are typically used in steady-state scenarios where values stabilize, parabolic equations often model diffusion processes over time, and hyperbolic equations are used to describe wave propagation. Knowing the type helps in predicting how solutions will evolve and behave in practical applications.
Examples & Analogies
Think of each classification as a different type of vehicle: an elliptical PDE is like a slow-moving bus that represents stability, a parabolic one is akin to a car speedily driving through city traffic, illustrating gradual change, while a hyperbolic PDE is like a speeding motorcycle—fast and dynamic as it cuts through air. Each vehicle navigates different terrains, just as each type of PDE navigates various physical scenarios effectively.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Discriminant: A crucial value that determines the classification of a second-order PDE.
-
Elliptic PDE: Describes phenomena where D < 0, reflecting steady states.
-
Parabolic PDE: Indicates D = 0, typical of evolving processes like heat diffusion.
-
Hyperbolic PDE: Denotes D > 0, often relating to wave motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Heat Equation, which is a parabolic PDE, models temperature changes over time.
-
Laplace's Equation serves as an example of an elliptic PDE, used in static field problems.
-
The Wave Equation illustrates a hyperbolic PDE and applies to wave phenomena in physics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Elliptic, steady and smooth; Heat is parabolic, a transient truth; Hyperbolic waves in flight, dancing with delight.
📖 Fascinating Stories
-
In a land of equations, Elliptic protects static fields, while Parabolic warms in transitions, and Hyperbolic creates ripples across the ocean sky.
🧠 Other Memory Gems
-
Remember P.E.H. for PDE types: Parabolic, Elliptic, Hyperbolic!
🎯 Super Acronyms
D.E.H. - D for discriminant, E for Elliptic, H for Hyperbolic.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Elliptic PDE
Definition:
A PDE where the discriminant D < 0, often associated with steady-state problems like Laplace's equation.
-
Term: Parabolic PDE
Definition:
A PDE where the discriminant D = 0, typically used in transient diffusion processes like the heat equation.
-
Term: Hyperbolic PDE
Definition:
A PDE where the discriminant D > 0, related to wave propagation, such as the wave equation.
-
Term: Discriminant
Definition:
A mathematical expression, D = B² - 4AC, used to classify second-order PDEs.