Types of Solutions of PDEs
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Complete Integral
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll discuss the concept of a complete integral in partial differential equations. Can anyone tell me what they think a complete integral refers to?

Is it a solution that contains all possible values?

Good start, but more specifically, a complete integral will have as many arbitrary constants as the order of the PDE. This means it represents a full set of solutions for that equation before any restrictions are applied.

So it’s the most general form of the solution then?

Exactly, Student_2! Remember this: Complete Integrals = Order of PDE in Arbitrary Constants. Can anyone give an example of a PDE where we might look for a complete integral?

Maybe Laplace’s equation or something similar?

Right! Both Laplace’s equation and the wave equation can provide complete integrals, serving as a foundation for building more specific solutions later on. Let’s summarize: Complete integrals match their arbitrary constants to the order of the PDE, and this makes them potent tools in solving PDEs.
General Solution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about the general solution. Who can explain what a general solution entails?

I think it has to do with using functions instead of constants, right?

Exactly! The general solution incorporates arbitrary functions, which allows it to adapt to various scenarios and initial conditions. It's like a toolbox with multiple tools to tackle different problems.

So how does this relate to the complete integral?

Great question! The general solution is broader than the complete integral because while the complete integral contains constants, the general solution uses functions. This adaptability is crucial for modeling real-world scenarios in engineering and physics.

Can you remind us again how we go from a general solution to a particular solution?

Of course! The transition to a particular solution is made by assigning specific values to the constants or functions in the general solution. To recap: General Solutions use arbitrary functions, allowing adaptability across scenarios.
Particular Solution
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s wrap up our discussion by looking at particular solutions. What do we need to do to find a particular solution from our general solution?

We need to choose some specific values for the constants or functions, right?

Yes! By substituting those specific values, we narrow down our general solution to something more specific and usable for particular cases. This makes the solution concrete and actionable in practice.

How important is it to note those values? Do they change the solution significantly?

Absolutely, the chosen values can significantly affect the outcome. It defines the particular conditions of the problem you're trying to solve. Remember: Particular Solutions = Specific Values from General Solutions.

So we generally start with complete integrals, move to general solutions, and then end with particular solutions?

Spot on! That progression is critical in solving partial differential equations effectively. Always keep in mind that every stage has its role, and understanding this flow can help you tackle more complex problems as we move forward.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
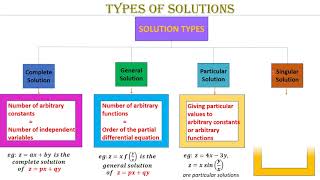
The section discusses the classification of solutions for PDEs into three types: complete integrals, which have as many arbitrary constants as the order of the PDE; general solutions, which encompass arbitrary functions; and particular solutions, obtained by assigning specific values to constants or functions. These definitions are crucial for understanding how to approach and solve PDEs in mathematical modeling.
Detailed
Types of Solutions of PDEs
In Partial Differential Equations (PDEs), solutions can be categorized into three primary types:
- Complete Integral: A complete integral of a PDE contains a number of arbitrary constants that matches the order of the PDE. This type is used to represent the most general solution of the equation before applying any specific conditions or values.
- General Solution: The general solution contains arbitrary functions instead of constants. It accounts for varying scenarios that a system might encounter, allowing for a broader application of the solution in real-world problems.
- Particular Solution: Obtained from the general solution, a particular solution is formulated by substituting specific values for the arbitrary constants or functions. This step is pivotal in obtaining a solution that is applicable to a given problem or scenario.
Understanding these types of solutions is essential in the study and application of PDEs, especially in fields like engineering and physics where such equations model complex phenomena.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Complete Integral
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Complete Integral: Contains as many arbitrary constants as the order of the PDE.
Detailed Explanation
A Complete Integral of a Partial Differential Equation (PDE) is defined as a type of solution that includes all possible variations of arbitrary constants. The number of arbitrary constants present in the solution corresponds to the order of the PDE; for a second-order PDE, there will be two arbitrary constants.
Examples & Analogies
Think of solving a mystery where the clues are your arbitrary constants. Depending on how complex the mystery is (like the order of the PDE), you might need several clues (arbitrary constants) to arrive at the complete picture of what happened (the complete integral).
General Solution
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- General Solution: Contains arbitrary functions.
Detailed Explanation
The General Solution of a PDE is more flexible than the Complete Integral. Instead of specific constants, it allows for arbitrary functions, which means that it can describe a broader set of solutions. This allows engineers and scientists to account for different scenarios based on varying conditions in their models.
Examples & Analogies
Imagine you are baking a cake and have a general recipe. Instead of a specific amount for sugar (a constant), the recipe lists 'a cup of sugar' (an arbitrary function). Depending on your taste or dietary needs, you can adjust this amount, creating different versions of the cake, just as the general solution creates different solutions based on varying parameters.
Particular Solution
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Particular Solution: Obtained by assigning specific values to constants/functions in the general solution.
Detailed Explanation
A Particular Solution is derived from the General Solution by substituting specific values for the arbitrary constants or functions. This yields a unique solution that fits certain boundary or initial conditions of the PDE. It helps provide exact solutions tailored to real-world scenarios.
Examples & Analogies
Think of a personalized customer service response. The general template for a response is the general solution, which can be adjusted based on different customer inquiries or scenarios. A Particular Solution is like responding specifically to one customer's concern by filling in their name and the details of their issue.
Key Concepts
-
Complete Integral: Solution with arbitrary constants matching PDE order.
-
General Solution: Includes arbitrary functions, adaptable to scenarios.
-
Particular Solution: Specific solution derived from general solution by setting constants/functions.
Examples & Applications
A complete integral of a second-order PDE might solve the wave equation and yield an expression with two arbitrary constants.
From a general solution of a heat equation, setting the constants to specific temperature values at a boundary gives a particular solution.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To solve PDEs, first find, a Complete Integral in mind; then use functions, so vast, General Solutions that will last; a Particular, just set some theme, turning equations into a dream.
Stories
In a mathematical land, there were three friends: Complete, General, and Particular. Complete knew all the secrets of PDEs like the back of his hand, containing constants galore. General liked to explore, using functions to adapt to any situation, while Particular would only come around when specific values were needed—making sense of the chaos!
Memory Tools
C-G-P: Complete integrals are for constants, General for functions, and Particular for specifics.
Acronyms
C.G.P - C for Complete Integral, G for General Solution, P for Particular Solution.
Flash Cards
Glossary
- Complete Integral
A solution of a partial differential equation that contains as many arbitrary constants as the order of the PDE.
- General Solution
A type of solution that includes arbitrary functions, allowing for more flexibility in applications.
- Particular Solution
A specific solution derived from the general solution by assigning particular values to its constants or functions.
Reference links
Supplementary resources to enhance your learning experience.
