Enrol to start learning
Reading is open to everyone. Enrolling is free, and it is what unlocks the audio lessons, practice tests and progress tracking.
16.5. Linear and Nonlinear PDEs
Learn content
Interactive Audio Lesson
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Let's start with linear PDEs. Can anyone tell me what makes a PDE linear?
Does it mean that the dependent variable and its derivatives appear only to the first power?
Exactly, great point! This means no products or higher powers of the variables or derivatives. For example, the equation is linear. Let's remember this with the acronym 'LDE', which stands for Linear Differential Equation.
Can you give another example of a linear PDE?
Sure! Another example is . It's linear because all terms are strictly to the first degree.
What about the solution methods for these equations?
Good question! Solutions for linear PDEs often involve superposition, meaning we can add solutions together. Remember, linearity allows us to handle these equations systematically.
Unlock the classroom podcast
The transcript is free to read. A free account plays the conversation back.
Now let's shift our focus to nonlinear PDEs. Who can give me the defining feature of a nonlinear PDE?
I think they include terms that are not linear, like products of derivatives or powers.
Spot on! An example of a nonlinear PDE can be given as . The term makes it nonlinear.
Why is this distinction important?
Great question! Nonlinear PDEs do not allow for superposition. This means that the methods to tackle them, such as numerical methods or specific ansatz, can be quite different from those used for linear PDEs.
How do we even approach solving these nonlinear equations?
We often rely on numerical methods or specific techniques devised for each unique case, as there's no one-size-fits-all strategy.
Overview
Short Summary
This section distinguishes between linear and nonlinear partial differential equations (PDEs), providing definitions and examples for each.
Medium Summary
The section elaborates on the characteristics of linear and nonlinear PDEs. Linear PDEs feature dependent variables and their derivatives appearing to the first degree, while nonlinear PDEs encompass terms that include products or powers of these variables and derivatives. Examples are provided to clarify the distinctions.
Detailed Summary
Linear and Nonlinear PDEs
In this section, we explore the critical concepts of linear and nonlinear partial differential equations (PDEs). A linear PDE is defined as an equation where the dependent variable and all its derivatives appear in a linear manner. For instance, an example of a linear PDE is
where the variable u and its derivatives are each to the first degree.
In contrast, a nonlinear PDE includes nonlinear terms, such as products or powers of the dependent variable or its derivatives. A classic example of a nonlinear PDE is
.
These distinctions are significant because the methods used to solve linear PDEs often differ significantly from those applied to nonlinear counterparts. Understanding whether a PDE is linear or nonlinear directly impacts the approaches taken for their solutions, which are foundational in the application of PDEs in diverse fields such as engineering and physical sciences.
Reference YouTube Videos
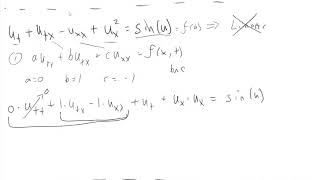
Audio Book
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account• Linear PDE: The dependent variable and all its derivatives appear linearly. Example: ∂u ∂2u =k ∂t ∂x2
Detailed Explanation
A linear PDE is characterized by the fact that the dependent variable, which is often denoted as 'u', and all of its derivatives, must only appear with a power of one. This means that there are no products of these quantities or any powers greater than one. The example provided shows a linear relationship as the equation involves the first derivative of 'u' with respect to time 't', and the second derivative with respect to 'x', combined linearly with a constant 'k'.
Examples & Analogies
Think of a linear relationship like a straight road. No matter how far you go, your path will always have the same slope, just like in a linear PDE where the derivatives influence the solution in a proportional way. For example, if the road represents temperature changes over time, then a linear equation would tell you that every degree change follows the same linear pattern.
Unlock the audio lesson
The script is above and free to read. A free account plays it back, in the voice you pick.
Create a free account• Nonlinear PDE: Involves nonlinear terms like products or powers of derivatives. Example: (cid:18) ∂u(cid:19)2 ∂u
- =0 ∂x ∂y
Detailed Explanation
A nonlinear PDE is defined by the presence of terms that involve products or higher powers of the dependent variable and its derivatives. In the provided example, the term (∂u/∂x)² indicates that the square of the first derivative with respect to x is part of the equation, which makes it nonlinear. This nonlinearity leads to more complex behavior and interactions in the system being modeled.
Examples & Analogies
Imagine trying to predict how water flows in a river. If the conditions change (for example, the rain makes the river swell), the behavior of the water becomes unpredictable — similar to how nonlinear PDEs behave. You might think of nonlinear relationships like a winding, uneven hiking trail that changes direction frequently as opposed to a straight road. The complexities found in nonlinear equations mimic the unpredictable patterns we observe in nature.
--
Key concepts
Core takeaways and short definitions to help you quickly recall the key ideas from this section.
- Linear PDE:
Defined by linearity in its dependent variable and derivatives.
- Nonlinear PDE:
Defined by the presence of nonlinear terms in the equation.
- Superposition:
A fundamental property utilized in solving linear PDEs.
Examples
Memory aids
Imagine a math wizard who can only wield his linear spells, but when he tries to mix them with nonlinear magic, chaos ensues and spells blend in strange ways!
Flash Cards
Glossary
Linear PDE
A partial differential equation where the dependent variable and its derivatives appear linearly.
Nonlinear PDE
A partial differential equation that includes nonlinear terms such as products or powers of the dependent variable and its derivatives.
Superposition
A property of linear systems where the sum of two solutions is also a solution.