Coordinates of a Vector
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Vector Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re going to discuss how vectors can be represented in terms of a basis of a vector space. If I have a vector space V, and a basis B with vectors v1, v2, ..., vn, how can we describe any vector v in that space?

Are you saying we can express any vector just using those basis vectors?

Exactly! We can write v as a linear combination of the basis vectors. This means v can be expressed as a1*v1 + a2*v2 + ... + an*vn, where a1, a2, ..., an are scalars. Can anyone tell me what these scalars represent?

They are like coordinates that tell us how much of each basis vector we need to reach the vector v!

Right! And the tuple (a1, a2, ..., an) is what we call the coordinate vector of v with respect to the basis B. It uniquely identifies the vector's position in the space.

So, can any vector be represented this way?

Yes, it’s a fundamental property of vector spaces! Each vector has a unique representation in terms of the basis. Let’s summarize: To find the coordinates of a vector in a space, express it as a linear combination of a given basis. Understanding this helps us in many practical applications.
Applications of Coordinate Vectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let us explore why understanding coordinate vectors is important. In what ways could the coordinate vector of a vector impact our work?

I guess it helps in understanding transformations, like when we manipulate the vector mathematically!

Exactly! Transformations such as rotation and scaling are easier to handle when working with coordinate vectors. Furthermore, in engineering, we can model physical systems more effectively using these coordinates.

Can you give an example of a field where this is used?

Certainly! In civil engineering, when analyzing forces acting on structures, engineers represent these forces using vectors. They then express these using coordinate vectors based on a chosen basis representing the physical dimensions of the structure. It’s essential for maintaining accuracy in calculations.

So, by knowing the coordinates we can easily do calculations without worrying about the visual representation?

Precisely! To conclude, working with coordinate vectors simplifies complex operations across various applications and streamlines problem-solving processes in numerous fields.
Creating Coordinate Vectors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s practice creating coordinate vectors. Suppose we have the basis B = {(1, 0), (0, 1)} for ℝ². If we have a vector v = (3, 4), how can we find the coordinates?

I guess we need to express it as a combination of the basis vectors. Here, v = 3*(1, 0) + 4*(0, 1). So the coefficients would be 3 and 4?

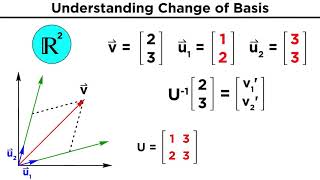
That’s correct! Thus, the coordinate vector for v using basis B is (3, 4). Now, if we changed the basis to B' = {(1, 2), (2, 1)}, how might the coordinates change?

We would have to solve for new coefficients using B', right?

Exactly! This shows that the representation of a vector can differ significantly depending on the chosen basis, even though it represents the same vector in the same space.

So, will practicing this help us in future courses?

Definitely! Mastering coordinate vectors is a foundation for more advanced topics, especially in linear algebra, computer graphics, and engineering. Let's remember: Coordinate vectors are unique representations linked to the basis.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section discusses how a vector can be uniquely represented with respect to a chosen basis of a vector space, utilizing the concept of coordinates. It highlights how the coefficients from the linear combination of basis vectors form the coordinate vector, and emphasizes the significance of this representation in understanding the vector's position and dimensions in the vector space.
Detailed
Coordinates of a Vector
In a vector space V with a basis B = {v1, v2, ..., vn}, any vector v ∈ V can be uniquely expressed as
v = a1v1 + a2v2 + ... + an*vn. The coefficients (a1, a2, ..., an) are called the coordinates of the vector v with respect to the basis B. This is a crucial concept since it allows us to understand how vectors can be represented and manipulated in a multidimensional space. The tuple formed by these coefficients, (a1, a2, ..., an), is termed the coordinate vector and plays a pivotal role in applications across various disciplines, including engineering, physics, and computer science. The coordinate vector not only gives the position of v in relation to the basis but also aids in various operations like linear transformations and mathematical modeling.
Youtube Videos






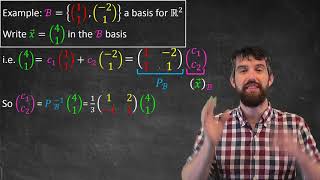
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Vector Representation
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Given a basis B={v_1,v_2,…,v_n} of a vector space V, any vector v∈V can be written uniquely as:
v=a_1 v_1 + a_2 v_2 + … + a_n v_n
Detailed Explanation
In a vector space, a vector can be expressed in terms of a specific set of basis vectors. The basis vectors (v_1, v_2, ..., v_n) can be thought of as the building blocks or reference points that define the space. The coefficients (a_1, a_2, ..., a_n) represent how much of each basis vector you need to construct a particular vector v. This representation is unique, meaning that for a given vector, there is only one combination of basis vectors that can achieve it.
Examples & Analogies
Consider the way we describe a location on a map using coordinates. Just as a point in a two-dimensional space can be described using x and y coordinates based on the axes, a vector can be expressed in terms of other vectors within the space using coefficients. For instance, if you say you're 3 units north and 4 units east of a starting point, those numbers are like the coefficients (a_1 and a_2) that tell you how much of each direction (the basis vectors) to take to reach your destination.
Coordinate Vector Definition
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The tuple (a_1, a_2,…,a_n) is called the coordinate vector of v with respect to the basis B.
Detailed Explanation
The coordinate vector is a concise way to represent the specific combination of basis vectors used to create a vector v. Each coefficient in this tuple corresponds to the magnitude of each basis vector included in that specific vector. By using the coordinate vector, we can easily handle operations like addition and scalar multiplication in vector spaces, as we are just manipulating the coefficients rather than the individual vectors themselves.
Examples & Analogies
Imagine you are mixing colors to paint a wall. Each color you use (like red, blue, yellow) represents a basis vector. The amount of each color you use (say 2 parts red, 3 parts blue) corresponds to the coefficients. The final color you create can be represented as a combination of those colors, just like a vector can be represented as a combination of basis vectors shown in the coordinate vector (2, 3) in this case.
Key Concepts
-
Coordinate Vector: A unique representation of a vector in terms of basis vectors, forming a tuple of coefficients.
-
Linear Combination: A mathematical method to express a vector as a sum of scaled basis vectors.
-
Basis: A foundational set of vectors allowing representation of any vector in a vector space.
Examples & Applications
Example 1: Given basis B = {(1, 0), (0, 1)} and vector v = (3, 4), the coordinate vector would be (3, 4) since v = 3(1, 0) + 4(0, 1).
Example 2: If we change the basis to B' = {(1, 2), (2, 1)}, we would need to find new coefficients to express v in terms of this new basis.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To find a vector's place, with basis give it grace! Coefficients align, to define the design.
Stories
Once upon a time, in a land of vectors, a brave vector named v set out to find its identity. It chose its allies, a basis named B. With B's help, v discovered it could express itself uniquely in the world of linear combinations.
Memory Tools
B. V. C. - Basis, Vectors, Coordinates. Remember the sequence to understand vector representation.
Acronyms
COORD - Coefficient Of Representation of a given Dimension.
Flash Cards
Glossary
- Coordinate Vector
The tuple of coefficients that express a vector as a linear combination of basis vectors in a vector space.
- Basis
A set of linearly independent vectors that spans a vector space, allowing any vector in the space to be expressed as a linear combination of basis vectors.
- Linear Combination
An expression constructed from a set of vectors where each vector is multiplied by a scalar and summed together.
- Vector Space
A mathematical structure formed by a collection of vectors that can be added together and multiplied by scalars.
Reference links
Supplementary resources to enhance your learning experience.
