Orthogonality in Vector Spaces
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonality
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're discussing orthogonality in vector spaces. Can anyone tell me what it means for two vectors to be orthogonal?

Are they at right angles to each other?

Exactly! Two vectors are orthogonal if their dot product equals zero. So, if I have vectors u and v, what is the condition for them to be orthogonal?

Their dot product must be zero.

Correct! This is important as it simplifies many calculations in linear algebra. Now, can anyone tell me why knowing orthogonal vectors is useful?

It helps us when finding bases for vector spaces.

Great point! Let's dive deeper into how orthogonality applies to sets of vectors.
Understanding Orthonormal Sets
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand orthogonality, let's discuss orthonormal sets. A set is orthonormal if every vector is orthogonal and of unit length. What does it mean for a vector to be a unit vector?

It has a length of one.

Exactly! Why do we care about orthonormal bases in practical applications?

They simplify computations, right?

Yes! Operations such as projections are much simpler with orthonormal bases. Can anyone name methods that use orthonormal bases?

The Gram-Schmidt process and QR factorization!

Well done! These methods are essential for numerical methods.
Application of Orthogonality
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's see how orthogonality applies to real-world problems. Can someone provide an example in engineering?

In structural analysis, if two forces are orthogonal, they don't influence each other?

Correct! This principle helps simplify the analysis. Lastly, how does orthonormality help in numerical computations?

It helps reduce errors and improves stability in algorithms.

Exactly! Remember, understanding orthogonality is crucial for effective problem solving in many fields.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the concept of orthogonality in vector spaces, where two vectors are orthogonal if their dot product equals zero. We also define orthonormal sets of vectors, which are orthogonal unit vectors, and discuss their applications in numerical methods and matrix decompositions, notably through processes such as Gram-Schmidt and QR factorization.
Detailed
Orthogonality in Vector Spaces
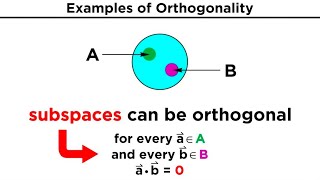
In linear algebra, two vectors u and v in R^n are said to be orthogonal if their dot product is zero: u � v = 0. This relationship provides a basis for understanding the geometric and algebraic interactions between vectors. A set of vectors is considered orthogonal if every pair of vectors in the set is orthogonal. Furthermore, if the vectors in this set are all unit vectors (vectors with a magnitude of one), the set is referred to as orthonormal.
Importance of Orthogonality
Orthonormal Basis
The concept of orthogonality is particularly useful in various numerical methods and matrix decompositions including:
- Gram-Schmidt process: This technique constructs an orthonormal basis from a set of linearly independent vectors. It ensures that subsequent vectors are orthogonal to previously identified vectors while maintaining their span.
- QR factorization: This method decomposes a matrix into an orthonormal basis, simplifying many computations such as solving linear equations or eigenvalue problems.
Orthonormal bases are especially valuable because they simplify calculations involving vector projections and transformations, providing an efficient and reliable framework for numerical analysis.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Orthogonality
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Two vectors
u,v∈ℝⁿ
are orthogonal if their dot product is zero:
u⋅v=0
Detailed Explanation
Orthogonality is a fundamental concept in vector spaces. It indicates that two vectors are orthogonal to each other if their dot product equals zero. This means that the angle between the two vectors is 90 degrees, meaning they are perpendicular to one another. In terms of their components, if you calculate the dot product (which involves multiplying corresponding components of the vectors and summing them up), a result of zero signifies orthogonality.
Examples & Analogies
Imagine two arrows (vectors) on a flat surface. If one arrow points directly up and the other points directly to the right, they create a 'T' shape, being at a right angle to each other. If you multiply their lengths in each direction and add up those products, you will find that they do not influence each other’s path, thus their dot product is zero.
Set of Orthogonal Vectors
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A set of vectors is orthogonal if every pair in the set is orthogonal.
Detailed Explanation
A group of vectors can be labeled orthogonal as a whole if every individual pair of vectors within the group holds the property of orthogonality. This means if you pick any two vectors from the set, their dot product will be zero. Orthogonal sets are particularly useful because they simplify calculations in various mathematical applications, like solving systems of equations or performing gradient calculations.
Examples & Analogies
Think about a coordinate grid where each direction—up, down, left, right—is represented by a vector. If you take one vector pointing up and another pointing right, they are orthogonal. If you had a whole set of directions—up, down, left, right—each pair from this set (e.g., up and down, left and right) remains orthogonal, making it a complete orthogonal set.
Orthonormal Set
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If they are also unit vectors, the set is orthonormal.
Detailed Explanation
An orthonormal set is a special case of orthogonal vectors. In addition to being orthogonal, each vector in an orthonormal set must have a length (or magnitude) of 1. This makes calculations involving these vectors simpler and more efficient, particularly in transformations and projections within vector spaces.
Examples & Analogies
Imagine a football field. The goal posts are spaced at equal distances apart and perpendicular to each other, creating an orthonormal set of guidelines to aim the ball. Each guide (like a vector) points in a specific direction, and when properly used (normed), they help maintain scoring accuracy, just as orthonormal vectors reduce complexity in calculations.
Orthonormal Basis
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A basis {v 1,v 2,…,v n} is orthonormal if:
{1 i=j
v ⋅v =
i j 0 i≠ j
Detailed Explanation
An orthonormal basis is a collection of vectors that are both perpendicular (orthogonal) and of unit length. The defining property is that for any two vectors in the basis, if you take their dot product, it will equal 1 when multiplied by itself (indicating unit length) and 0 when multiplied by any other vector (indicating orthogonality). This orthonormal basis simplifies many calculations in linear algebra, making it easier to work with vector representations and transformations.
Examples & Analogies
Think of a standard chessboard. Each row and column of squares represents a unit vector in an orthonormal basis, providing clear pathways for moves (transformations). Each piece follows orthogonal paths: the rook moves straight, the knight jumps, each unique and distinct while remaining within the orthonormal structure of the board.
Applications of Orthogonality
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Useful in numerical methods (e.g., Gram-Schmidt process) and matrix decompositions (e.g., QR factorization).
Detailed Explanation
Orthogonality is crucial in various mathematical methods, especially in numerical analysis and linear algebra. The Gram-Schmidt process, for instance, is a method that takes a set of vectors and orthogonalizes them, creating an orthonormal basis. Similarly, in QR factorization, a matrix can be decomposed into an orthogonal matrix Q and an upper triangular matrix R, which simplifies solving systems of equations and optimizing computations.
Examples & Analogies
Consider a well-organized toolbox. Each tool has a specific function and does not interfere with the others (like orthogonal vectors). When you organize your toolbox (using methods like Gram-Schmidt), you ensure that tools (vectors) are easy to reach (optimally computed) and that they perform tasks efficiently—illustrating how orthogonality improves process efficiency in numerical applications.
Key Concepts
-
Orthogonality: Two vectors are orthogonal if their dot product is zero.
-
Orthonormal Set: A orthonormal set consists of vectors that are both orthogonal and of unit length.
-
Applications: Orthogonality is crucial in numerical methods and matrix decompositions.
Examples & Applications
Vectors (3, 4) and (4, -3) are orthogonal because their dot product is 34 + 4(-3) = 0.
The set of vectors {(1, 0), (0, 1)} is orthonormal and commonly used as the basis for R².
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Orthogonal vectors, they don’t collide, their dot product is zero, staying side by side.
Stories
Imagine a dance floor where dancers (vectors) avoid bumping into each other; that’s orthogonality! When they move in different directions without interference, they’re orthogonal!
Memory Tools
To remember orthonormal, think ‘Orthogonal is Normal!’ (O for Orthogonal, N for Normal).
Acronyms
O.B.S. for Orthonormal Basis Set - remember it stands for Orthogonal and Unit vectors.
Flash Cards
Glossary
- Orthogonal
Vectors u and v are orthogonal if their dot product u⋅v equals zero.
- Orthonormal
A set of vectors is orthonormal if each vector has a unit length and is orthogonal to every other vector in the set.
- Dot Product
An algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number.
- Basis
A set of vectors that can be combined to express every vector in a given vector space.
- GramSchmidt Process
An algorithm for orthogonalizing a set of vectors in an inner product space.
Reference links
Supplementary resources to enhance your learning experience.
