Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Exploring ℝⁿ
Unlock Audio Lesson
Today, we're discussing an essential example of vector spaces: ℝⁿ, or n-dimensional real space. Can anyone tell me what an n-tuple looks like?
Is it like a collection of n numbers, such as (x₁, x₂, ..., xₙ)?
Exactly! Each of these n-tuples can be added together, and you can scale them by real numbers. This sets the groundwork for the vector space properties. Can you recall the closure property?
Oh, does it mean that if we add two vectors from ℝⁿ, the result is still in ℝⁿ?
Correct! That’s closure under addition. Keep that in mind as we explore more examples today.
Functions as Vector Spaces
Unlock Audio Lesson
Next, let’s consider the set of all real-valued functions. Can anyone give me an example of a real-valued function?
How about f(x) = x²?
Good example! This set of functions can also form a vector space if we apply function addition and scalar multiplication. Can you see how these operations are defined?
If I add f(x) = x² and g(x) = x + 1, the result is h(x) = x² + x + 1, right?
Exactly! And importantly, if you scale it with a constant, say 3, you would get 3h(x) = 3x² + 3x + 3. Both results remain within our space. That’s fundamental!
Matrices as Vector Spaces
Unlock Audio Lesson
Now, let’s delve into the set of m×n real matrices. Are you all familiar with how matrix addition works?
Yes, it involves adding corresponding elements from each matrix.
Correct! This composition along with scalar multiplication makes it a vector space. Can you visualize its span?
I picture it like a grid where each point represents a matrix, and addition produces a new point in the same grid.
Great visualization! Understanding these operations reinforces that this space adheres to vector space properties.
Polynomials as Vector Spaces
Unlock Audio Lesson
Finally, let’s examine the set of all polynomials of degree ≤ n. Why do you think this qualifies as a vector space?
Because we can add them and multiply by scalars, making sure the result is still a polynomial of the same degree!
Exactly! Not only do they meet the closure property, but they also span a space based on their degree. Let's consider some practical applications of these vector spaces.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In Section 24.2, we delve into specific examples of vector spaces, such as ℝⁿ (n-dimensional real space), the space of real-valued functions, the set of m×n matrices, and the space of polynomials of degree ≤ n. Each example illustrates the defining properties and operations that qualify these sets as vector spaces.
Detailed
Examples of Vector Spaces
Vector spaces are fundamental in the study of mathematics and engineering, and this section outlines several examples to illustrate their concepts:
- ℝⁿ (n-dimensional real space):
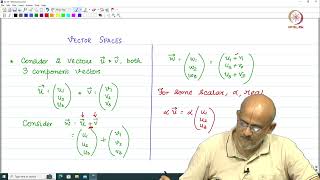
- Each element is represented as an n-tuple of real numbers, forming a vector space under standard addition and scalar multiplication.
- Set of all real-valued functions:
- This set consists of functions from real numbers to real numbers. It is a vector space where function addition and scalar multiplication adhere to vector space axioms.
- Set of m×n real matrices:
- The collection of all m × n matrices behaves as a vector space under the operations of matrix addition and scalar multiplication.
- Set of polynomials of degree ≤ n:
- This space includes all polynomials with real coefficients up to a specified degree, demonstrating the properties of a vector space and leading to vital applications in various fields.
These examples illustrate how diverse mathematical structures can be understood within the framework of vector spaces, emphasizing their applications in linear algebra and engineering.
Youtube Videos
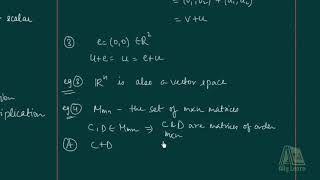
Audio Book
Dive deep into the subject with an immersive audiobook experience.
ℝⁿ (n-dimensional real space)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- ℝⁿ (n-dimensional real space)
Each element is an n-tuple: (x 1,x 2,…,x n) with real components.
Detailed Explanation
In this chunk, we are introduced to ℝⁿ, which denotes n-dimensional real space. This means that any point in this space can be represented as an ordered set of numbers, or an 'n-tuple'. Each number corresponds to a dimension in that space. For example, in a 2-dimensional space (ℝ²), a point would be expressed as (x₁, x₂), representing coordinates on a plane.
Examples & Analogies
Think of walking in a city. Every address can be represented with two numbers: one for how far you go down the street (x₁) and another for how far you go across (x₂). Similarly, in ℝⁿ, we can find our position in 'n' dimensions just like finding an address in a grid.
Set of all real-valued functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Set of all real-valued functions
Let V be the set of all real-valued functions f:ℝ→ℝ. Then V is a vector space with function addition and scalar multiplication.
Detailed Explanation
In this chunk, we examine a vector space consisting of real-valued functions defined from the real numbers (ℝ) to real numbers (ℝ). This means each element in this vector space is a function. The operations of vector space (addition and scalar multiplication) can be applied to these functions. Specifically, you can add two functions together or multiply a function by a scalar (a real number).
Examples & Analogies
Consider a simple example of temperature over time represented as a function. If one function shows temperature data for one week and another shows data for another week, you could add these functions together to create a new function representing total temperature. This demonstrates how we can work with functions in vector spaces!
Set of m×n real matrices
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Set of m×n real matrices
The set M m×n(R) of all m×n matrices forms a vector space under matrix addition and scalar multiplication.
Detailed Explanation
Here, we learn about a vector space formed by sets of matrices, specifically m-by-n matrices, which are rectangular arrays of numbers. Just like we can add vectors or scale them up or down, we can do the same with matrices. The addition involves adding corresponding elements in two matrices, while scalar multiplication means multiplying every element in the matrix by a single number.
Examples & Analogies
Imagine matrices as tables with grades for different subjects across various students. If each student’s grades are captured in a matrix, you can easily combine two students' grades via matrix addition to analyze performance together. Similarly, adjusting each score (scalar multiplication) lets you predict scores with different grading scales.
Set of polynomials of degree ≤ n
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Set of polynomials of degree ≤ n
The set of all polynomials with real coefficients and degree ≤ n is a vector space.
Detailed Explanation
This chunk presents polynomials as vectors. A polynomial is generally a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients. Here, we're considering polynomials that can go up to degree n, meaning the highest exponent of the variable can be n. This set forms a vector space when you can add two polynomials or multiply one by a scalar while still yielding another polynomial of the same form.
Examples & Analogies
Think of a polynomial as a recipe that includes several ingredients (coefficients) and how much of each ingredient you can include (the powers of variables). Just like you can add two recipes together to create a new one or scale the ingredients (by a number), we can mix and scale polynomials in this vector space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
n-dimensional real space: The space of all ordered n-tuples of real numbers forming a vector space.
-
Set of real-valued functions: A vector space comprised of all functions mapping real numbers to real numbers.
-
Set of m×n matrices: A collection of matrices of size m by n that operate under matrix addition and scalar multiplication.
-
Polynomials of degree ≤ n: A vector space that includes all polynomials of a degree up to n with real coefficients.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: ℝ² consists of all ordered pairs of real numbers, like (x, y).
-
Example 2: The set of all linear functions f(x) = ax + b forms a vector space.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For vectors in space, we follow the rules, addition and scaling make us wise tools.
📖 Fascinating Stories
-
Imagine a classroom where every student is a vector. When they cooperate (add) and respond to instructions (scalar multiplication), they all stay in the same classroom (the vector space).
🧠 Other Memory Gems
-
Remember the acronym 'FAME' for vector spaces: Functions, Addition, Matrices, and Elements.
🎯 Super Acronyms
V.S.P. - Vectors in Spaces Practice
- visualize
- solve
- and prove.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Space
Definition:
A set V equipped with operations of vector addition and scalar multiplication satisfying certain axioms.
-
Term: ntuple
Definition:
An ordered collection of n elements, commonly represented as (x₁, x₂, ..., xₙ) in ℝⁿ.
-
Term: Closure Property
Definition:
The property stating that an operation performed on elements of a set will yield an element also in the set.