Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Row and Column Space
Unlock Audio Lesson
Today, we are discussing two important concepts: row space and column space. Let's start with row space. Can anyone tell me what the row space of a matrix represents?
Is it the set of all possible linear combinations of the row vectors?
Exactly! The row space captures all linear combinations of the row vectors of a matrix. This makes it a subspace of the vector space R^n. Now, how about the column space? What do we know about it?
The column space is the span of the column vectors of the matrix?
Correct! The column space includes all possible linear combinations of the columns. It forms a subspace in R^m. Remember: Row space relates to rows, and column space relates to columns.
How do we use these concepts in practical problems?
Great question! They are often used to determine the rank of a matrix, which tells us about the number of linearly independent rows or columns. Let's hold onto that thought.
So, rank can give us insights into the system of equations that we can solve with this matrix?
Absolutely! Summarizing, the row space and column space help us understand the effects of a matrix in terms of linear transformations.
Exploring Null Space
Unlock Audio Lesson
Now, let's dive into the null space. What can you tell me about it?
The null space is the set of vectors that make the equation Ax = 0 true, right?
Exactly! The null space contains all solutions to that equation, making it a vital aspect of linear algebra. Why do you think it’s important?
It shows us which vectors get mapped to the zero vector under the transformation defined by A.
Right again! The null space represents the directions along which the transformation collapses. Can anyone think of a geometric interpretation?
I think it could represent a flat region in space where all points get mapped to zero.
That's an excellent visualization! Summarizing, the null space provides comparative information on the range of the transformation and the underlying solution structure.
Connections Between Spaces
Unlock Audio Lesson
Let’s combine what we've learned and discuss how row space, column space, and null space connect to each other.
Are they all subspaces of R^n or R^m?
Good point! Row and column spaces are subspaces of R^n and R^m, respectively, while the null space is a subspace of R^n. Now, can anyone share how the dimension of these spaces relates to each other?
I remember that the Rank-Nullity Theorem might play a role here.
Exactly! The Rank-Nullity Theorem states that the Rank of A plus the Nullity of A equals n, where n is the number of columns in A. This ties together what we've just learned about these spaces.
So, the dimension of the column space plus the dimension of the null space gives us the total number of columns?
Spot on! To summarize, understanding these relationships is essential in solving linear equations and analyzing transformations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Row space and column space represent the span of the row and column vectors of a matrix, respectively, while the null space consists of all solutions to the equation Ax = 0. Each of these is a subspace, and together they play a crucial role in understanding the properties and behavior of matrices in linear algebra.
Detailed
Row Space, Column Space, and Null Space
In linear algebra, for any given matrix A of size m × n, three fundamental subspaces are defined: the row space, the column space, and the null space.
Key Points:
- Row Space: The row space of matrix A is defined as the span of its row vectors. This implies that it includes all possible linear combinations of the row vectors, forming a subspace within the vector space R^n.
- Column Space: Similarly, the column space is the span of the column vectors of matrix A. This subspace is comprised of all linear combinations of the column vectors and is contained in R^m.
- Null Space: The null space of matrix A consists of all vectors x in R^n that satisfy the equation Ax = 0. This set of solutions forms a subspace of R^n. It represents the directions in which the transformation defined by matrix A collapses to the zero vector.
Each of these spaces plays a critical role in understanding the matrix's rank and degree of freedom in solutions to linear systems. Together, they provide insights into the fundamental properties of linear transformations and their geometrical interpretations.
Youtube Videos
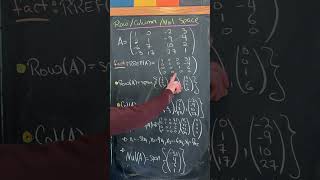
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to A Matrix A
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let A be an m×n matrix.
Detailed Explanation
This chunk introduces the idea of a matrix, denoted as A, which has m rows and n columns. The concept of matrix dimensions is crucial in understanding the interactions between different vector spaces that this chapter will explore. In simple terms, m is the number of horizontal lines of numbers, and n is the number of vertical columns.
Examples & Analogies
Think of a matrix like a spreadsheet. Each row can represent a different data entry (like a person or an event), while each column can represent different attributes (such as name, age, height). This organization makes it easier to analyze the data.
Row Space of A
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The row space of A: span of the row vectors.
Detailed Explanation
The row space of a matrix A is defined as the span of its row vectors. This means that the row space consists of all possible linear combinations of the rows of the matrix A. If we visualize this, each row vector can be thought of as a direction in space, and the row space represents all the different ways you can combine these directions to create new vectors. Essentially, it captures all outcomes that can be expressed as combinations of the rows.
Examples & Analogies
Imagine you have several ropes of different lengths, and you can tie them together in various ways. The row space represents all the different shapes you can form by connecting these ropes. Each new shape is a combination of the original rope lengths.
Column Space of A
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The column space of A: span of the column vectors.
Detailed Explanation
The column space of A is similarly defined as the span of the column vectors. It consists of all possible linear combinations of the columns of the matrix A. Visualizing this concept, if the rows represent one set of directions, the columns represent another. The column space captures all possible outcomes that can be achieved through combinations of the column vectors.
Examples & Analogies
Think of each column vector as a distinct tool in a toolbox. The column space is like the range of different constructions you can build by using various combinations of these tools. The more tools you have, the more complex and varied your constructions can be.
Null Space of A
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The null space of A: set of all solutions x∈Rn to Ax=0.
Detailed Explanation
The null space of the matrix A consists of all vectors x in ℝⁿ that satisfy the equation Ax = 0. This means that when the matrix A multiplies the vector x, you end up with the zero vector. The null space is a crucial concept because it identifies all the possible solutions that lead to no net effect (the zero outcome) when combined with the linear transformation represented by the matrix A.
Examples & Analogies
Imagine you have a see-saw (or a balance scale) that is perfectly balanced when no additional weights are added. The null space represents all the possible positions that keep the scale level, which could include various weights placed in different positions. If you think of each position and weight as a vector, the null space captures all configurations that won't tip the see-saw.
Subspaces Defined by Row, Column, and Null Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each of these is a subspace of a suitable vector space.
Detailed Explanation
The row space, column space, and null space identified earlier are not just abstract concepts but are specific examples of subspaces. A subspace in linear algebra must satisfy certain criteria, such as containing the zero vector, closed under addition, and closed under scalar multiplication. All three spaces — row, column, and null — fulfill these criteria, making them legitimate subspaces of vector spaces associated with the matrix A.
Examples & Analogies
Consider a large room (vector space) where various sections (subspaces) are defined by walls (the row, column, and null spaces). Each section can hold various objects (vectors), but together they must maintain the characteristics of the room, such as the ability to move freely without leaving the room and without altering the room's overall structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Row Space: The span of the rows of a matrix.
-
Column Space: The span of the columns of a matrix.
-
Null Space: The set of vectors that satisfy Ax = 0.
-
Rank: The dimension of the column space.
-
Nullity: The dimension of the null space.
-
Rank-Nullity Theorem: A relationship between rank, nullity, and the number of columns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of Row Space: Given a matrix A = [[1, 2, 3], [4, 5, 6]], the row space is spanned by vectors [1, 2, 3] and [4, 5, 6].
-
Example of Null Space: For matrix A = [[1, 2], [3, 6]], the null space includes all vectors x such that Ax = 0, forming a subspace.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In space, each row shows its grace, with column combinations in their place.
📖 Fascinating Stories
-
Imagine a map with points where you can walk. Each step in a row leads to new stops, but in the null space, you find spots where you can’t go any further.
🧠 Other Memory Gems
-
Remember: RCN - Row, Column, Null to navigate the key spaces in matrices.
🎯 Super Acronyms
Use 'RNC' (Row-Null-Column) to recall the order of matrix subspaces.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Row Space
Definition:
The span of the row vectors of a matrix.
-
Term: Column Space
Definition:
The span of the column vectors of a matrix.
-
Term: Null Space
Definition:
The set of all solutions to the equation Ax = 0.
-
Term: Subspace
Definition:
A subset of a vector space that is also a vector space under the same operations.
-
Term: Rank
Definition:
The dimension of the column space of a matrix.
-
Term: Nullity
Definition:
The dimension of the null space of a matrix.
-
Term: RankNullity Theorem
Definition:
A theorem that states Rank(A) + Nullity(A) = n for an m × n matrix A.