Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vector Spaces
Unlock Audio Lesson
Welcome everyone! Today, we're diving into vector spaces. Can anyone tell me what a vector space might be?
Isn't it just a set of vectors?
That's a good start! A vector space is indeed a set of vectors but also requires specific operations, namely vector addition and scalar multiplication. We usually look at vector spaces over a field, like the real numbers.
What types of operations are involved in this context?
Great question! The two operations are vector addition, which takes two vectors and combines them, and scalar multiplication, which scales a vector by a number. There are axioms we have to abide by as well. Can anyone name one?
Is closure under addition one of those axioms?
Exactly! Closure under addition means that when you add two vectors from the space, the result must still be in that space. Let's remember it through the acronym 'CATS': Closure, Addition, and The Space remains!
How does this apply in civil engineering?
Vector spaces are crucial in civil engineering. They help model complex systems like forces and displacement. Understanding these principles lays the groundwork for analyzing structures effectively.
In summary, today we learned that vector spaces are structured sets with operations that must obey specific rules, crucial for both mathematics and real-world applications like engineering.
Axioms of Vector Spaces
Unlock Audio Lesson
Let's go through the axioms of vector spaces. Who remembers the fundamental aspects that these axioms cover?
There are rules about addition and multiplication?
Exactly! The axioms include closure under addition, commutativity of addition, associativity of addition, and others related to scalar multiplication. Each of these rules ensures the structure of the vector space is maintained.
Can you give an example of closure under addition?
Sure! If you take two vectors, say v and u, from the vector space V, and add them together, the resulting vector u+v must also be in V. This property is essential—like keeping all your toys in the same toy box!
What’s the importance of the additive identity?
The additive identity axiom states there must be a vector, often called the zero vector, in V such that when you add it to any vector v, it doesn’t change v. It's like keeping a secret—the zero vector keeps the value unchanged.
To summarize, the axioms for vector spaces define how we can combine vectors and how they interact with scalars, laying the groundwork for exploring more complex concepts.
Applications of Vector Spaces
Unlock Audio Lesson
Now, let's connect the dots to the real world. How do vector spaces relate to civil engineering?
They help in structural analysis, right?
Absolutely! In structural analysis, we model forces and displacements as vectors in a vector space. This enables us to understand how structures react under various loads.
So, if I understand it correctly, if I add forces applied at different points, I can still work within that vector space?
Exactly! By ensuring all operations stay within the vector space, we can simplify complex equations that help predict structural behavior. Remember the term 'Span'; it refers to all combinations of those vectors!
This makes sense. I see how those concepts link back to our engineering challenges.
In conclusion, the frameworks provided by vector space theories not only apply within mathematics but extend to real-world problems in engineering, enhancing our problem-solving capabilities.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we define a vector space as a set equipped with operations of vector addition and scalar multiplication. We also outline the axioms that ensure these operations function within the space, providing a foundational understanding necessary for more complex topics in mathematics and engineering.
Detailed
A vector space, also known as a linear space, is defined as a set V along with two operations: vector addition and scalar multiplication. For V to be considered a vector space over a field F (often the field of real numbers ℝ), it must satisfy a series of axioms which include closure under addition, commutativity, associativity, and the existence of identity and inverse elements for vector addition. Additionally, the operations must follow specific distributive and associative properties relevant to scalar multiplication. Understanding these axioms is crucial for a deeper grasp of linear algebra, as they provide the framework for working with higher-level mathematical constructs and their applications in engineering, such as modeling physical systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Vector Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
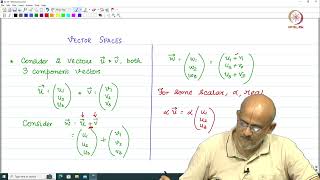
A vector space (also called a linear space) over a field F (usually the field of real numbers ℝ) is a set V equipped with two operations:
- Vector addition: +:V ×V →V
- Scalar multiplication: ⋅:F×V→V
Detailed Explanation
A vector space is a collection of objects called vectors, which can be added together and multiplied by numbers (scalars). The field F is typically the set of real numbers, ℝ. The two operations defined in a vector space are vector addition and scalar multiplication. Vector addition combines two vectors to produce another vector from the same space, while scalar multiplication involves multiplying a vector by a scalar, yielding another vector in the same space.
Examples & Analogies
Think of a vector space like a collection of arrows in a two-dimensional plane. Each arrow represents a vector. When you add two arrows head-to-tail, you get a new arrow (the resultant vector). If you scale an arrow (make it longer or shorter), you still have an arrow, just a different one that points in the same direction.
Axioms of Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
such that the following axioms hold for all u,v,w∈V and all scalars a,b∈F:
1. Closure under addition: u+v∈V
2. Commutativity of addition: u+v=v+u
3. Associativity of addition: (u+v)+w=u+(v+w)
4. Existence of additive identity: There exists a vector 0∈V such that v+0=v
5. Existence of additive inverse: For each v∈V, there exists −v∈V such that v+(−v)=0
6. Closure under scalar multiplication: a⋅v∈V
7. Distributivity over vector addition: a⋅(u+v)=a⋅u+a⋅v
8. Distributivity over scalar addition: (a+b)⋅v=a⋅v+b⋅v
9. Associativity of scalar multiplication: a⋅(b⋅v)=(ab)⋅v
10. Identity scalar multiplication: 1⋅v=v, where 1 is the multiplicative identity in F.
Detailed Explanation
The axioms of vector spaces define the essential properties that vectors must satisfy for the set to be a vector space. These axioms ensure that vector addition and scalar multiplication yield results that are also in the set. For example, closure under addition means that when you add any two vectors, the result is still a vector in the same space. Associativity and commutativity describe how addition works. The existence of an additive identity means there's a vector (the zero vector) such that adding it to any vector does not change the vector. The existence of an additive inverse means for every vector, there is another vector that adds to the zero vector.
Examples & Analogies
Imagine a basketball team where each player's skills represent a vector. The team as a whole is the vector space. If two players combine their skills (like adding vectors), the team's skills reflect their combined efforts (closure under addition). If you swap the players' roles when evaluating skills (commutativity), it doesn't change the outcome. Everyone contributes their individual strengths (associativity and additive identities), while everyone also has areas they can improve (additive inverses).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Space: A set with addition and scalar multiplication operations.
-
Axioms: Fundamental rules that govern operations in a vector space.
-
Closure: A property ensuring results of operations remain within the vector space.
-
Scalar Multiplication: Multiplying a vector by a scalar.
-
Additive Identity: The zero vector that does not change other vectors when added.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
ℝⁿ (n-dimensional real space) is a vector space where each element is an n-tuple with real components.
-
The set of all real-valued functions f:ℝ→ℝ forms a vector space under function addition and scalar multiplication.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a vector space so fine, add and scale, everything aligns!
📖 Fascinating Stories
-
A set of brave vectors ventured out, knowing they'd always stay within their bounds, as every time they added or scaled, they'd never stray from their home space!
🧠 Other Memory Gems
-
Remember CATS: Closure, Addition, True Space conditions must hold in every place!
🎯 Super Acronyms
V.A.S.E
- Vector Space Adds Scalar Ensuring closure is key!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Space
Definition:
A set V equipped with two operations: vector addition and scalar multiplication, satisfying specific axioms.
-
Term: Axioms
Definition:
A set of rules governing the operations in a vector space.
-
Term: Closure
Definition:
A property indicating that the result of an operation on elements of a set will also belong to that set.
-
Term: Scalar Multiplication
Definition:
The operation that multiplies a vector by a scalar, resulting in another vector in the space.
-
Term: Additive Identity
Definition:
A special element in a vector space that, when added to any vector, returns the unchanged vector.