Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Defining Subspace
Unlock Audio Lesson
Today, we're diving into the concept of subspaces. Remember, a subspace is a non-empty subset of a vector space that is also a vector space itself. Can anyone tell me what conditions we need to check to confirm that a subset is a subspace?
Does it have to contain the zero vector?
Exactly! The zero vector must be present. That brings us to our first condition. There are actually three to remember. Who can name the other two?
It needs to be closed under addition and scalar multiplication.
Great! Think of the acronym CAS, which stands for Closure(under addition) and Scalar multiplication to help remember these criteria.
Example of a Subspace
Unlock Audio Lesson
Let’s apply what we've learned. We have the vector space V as R³ and W defined as all points satisfying the equation x + y + z = 0. How do we verify if W is a subspace?
First, we check if the zero vector is in W. The zero vector is (0, 0, 0), and that satisfies the equation.
Correct! Now, what about checking the closure under addition?
If we take two vectors from W, say (x1, y1, z1) and (x2, y2, z2), their sum is (x1+x2, y1+y2, z1+z2), and we can show it satisfies the equation too.
Excellent observation! Remember that demonstrating these properties can confirm whether W is indeed a subspace.
Importance of Subspaces
Unlock Audio Lesson
Subspaces are essential for understanding more complex ideas like the span of vectors and linear independence. Why do you think it's important for engineers to understand these concepts?
I think it helps in optimizing solutions and models in engineering, especially in structural analysis.
Yes, subspaces can represent constraints in designs!
Exactly! Subspaces help engineers to simplify problems and focus on essential dimensions of a system.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
A subspace of a vector space is defined as a non-empty subset that is also a vector space under the same operations. This section emphasizes conditions such as containing the zero vector, closure under addition, and closure under scalar multiplication, providing a practical example for clarity.
Detailed
In linear algebra, a subspace is a crucial concept within vector spaces. Specifically, a subspace W of a vector space V is characterized as a non-empty subset that is a vector space itself, employing the same operations found in V. To qualify as a subspace, a set W must satisfy three conditions:
1. The zero vector (0) must be in W.
2. The sum of any two vectors in W must also belong to W.
3. Any scalar multiple of a vector in W must also remain in W.
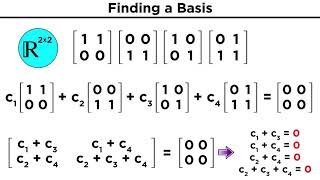
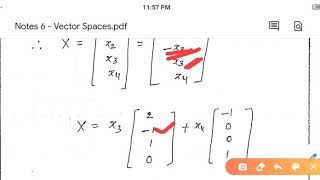
For instance, considering V as R³, the set W defined by the equation { (x, y, z) ∈ R³ : x + y + z = 0 } exemplifies a subspace of R³. Understanding subspaces is vital as they form the foundation for more advanced concepts such as linear combinations, span, and dimension, which are instrumental in engineering and mathematical modeling.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Subspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A subspace of a vector space V is a non-empty subset W of V that is itself a vector space under the same operations.
Detailed Explanation
A subspace is essentially a smaller vector space contained within a larger vector space. To qualify as a subspace, a subset must meet specific conditions: it is non-empty, and it must adhere to the same rules of vector addition and scalar multiplication that apply to the larger vector space. In simpler terms, if you can take any two vectors from this subset and add them together, and if you can take any vector from the subset and multiply it by a scalar (a number), and both results still belong to the subset, then the subset is indeed a subspace.
Examples & Analogies
Imagine you have a large box (the vector space) filled with different shapes (the vectors). If you take out a smaller box within the large box and fill it only with certain types of shapes—say only circles—that smaller box is like a subspace. As long as you can stack circles on top of each other (addition) and stretch them larger (scalar multiplication), that smaller box maintains its properties as a vector space.
Conditions for Subspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let W⊆V. Then W is a subspace if:
1. 0∈W
2. u,v∈W⇒u+v∈W
3. a∈R,v∈W⇒a⋅v∈W
Detailed Explanation
For a subset W to qualify as a subspace of V, it must satisfy three critical conditions. First, it must contain the zero vector (0), which represents no movement or change. Second, if you take any two vectors (u and v) from W, their sum (u + v) must also be in W. Lastly, multiplying any vector in W by a scalar (a real number) must result in another vector that still belongs to W. These three properties ensure that W behaves similarly to a vector space, maintaining the internal structure and operations of vector addition and scalar multiplication.
Examples & Analogies
Think of a sports team (the vector space), where every player is a vector. The zero vector corresponds to an empty team, where no player is included (0). If every time two players (u and v) decide to collaborate (add), they still play for the same team (u + v ∈ W), and if when the coach (the scalar) encourages any player to improve their game (a⋅v), they still belong to the team (a⋅v ∈ W), then we know our team follows the same dynamics expected in the larger sports world.
Example of Subspace
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let V=R³ and W={(x, y,z)∈R³:x+y+z=0}. Then W is a subspace of R³.
Detailed Explanation
In this example, we consider R³, which is a three-dimensional vector space consisting of all possible ordered triples of real numbers (x, y, z). The set W defined by the equation x + y + z = 0 includes all points in R³ that lie on a specific plane intersecting the origin (0,0,0). To verify W as a subspace, we can check the three conditions: 1) The zero vector (0,0,0) is in W because 0 + 0 + 0 = 0. 2) Adding any two vectors in W will satisfy the condition because the sum of their coordinates will still yield zero. 3) Multiplying any vector from W by a scalar will not change the fact that the sum of their coordinates is still zero.
Examples & Analogies
Imagine integrating certain resources (like ingredient quantities in a recipe) where you measure how much of each ingredient you have. If the total measurement of all ingredients must equal zero (in our W, this is analogous to balancing flavors), then every time you add or adjust these quantities, they must still follow that rule (remaining in W), just as a professional chef needs to maintain a balanced recipe without going off course. This ensures that whatever combination you have (the subspace), it remains consistent with achieving the desired flavor balance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Subspace: A subset of a vector space that is itself a vector space.
-
Closure: The property that results of operations remain within a set.
-
Zero Vector: The vector in any vector space where all components are zero.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
W = {(x, y, z) ∈ R³ : x + y + z = 0} is a subspace of R³ because it contains the zero vector and is closed under addition and scalar multiplication.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a vector space, a subspace shines, zero is key, and closure aligns.
📖 Fascinating Stories
-
Imagine a family of vectors, where the zero vector is the parent. All children (vectors) must add up to the family home (the subspace).
🧠 Other Memory Gems
-
C.A.S (Closure under Addition and Scalar multiplication) helps you remember key subspace criteria!
🎯 Super Acronyms
Z.A.C, for Zero, Addition, Closure which the subspace needs to have!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Subspace
Definition:
A subset W of a vector space V that is itself a vector space under the same operations.
-
Term: Closure
Definition:
A property indicating that the result of an operation (such as addition) on elements from a set remains within that set.
-
Term: Zero Vector
Definition:
A vector with all components equal to zero, serving as the additive identity in vector spaces.