Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vector Space Isomorphism
Unlock Audio Lesson
Today, we'll explore vector space isomorphism. Can anyone tell me what an isomorphism might mean in mathematical terms?
I think it means that two structures are similar in some way.
Absolutely! In the context of vector spaces, we define an isomorphism as a bijective linear map between two spaces. It indicates they are structurally identical. Now, what does bijective mean?
It means that there is a one-to-one correspondence between elements of the two spaces.
Exactly! So, if we have two vector spaces, V and W, and a bijective linear map T: V → W, we can say these spaces are isomorphic.
Properties of Isomorphisms
Unlock Audio Lesson
Now, let's delve into the implications of having an isomorphism. If T is an isomorphism, what can you infer about the dimensions of these vector spaces?
If they are isomorphic, they must have the same dimension.
Correct! Therefore, if dimV = dimW = n, this suggests that 'V is isomorphic to R^n'. This statement opens doors to understanding vector spaces across multiple applications. Can anyone think of how this might be useful?
It might help in simplifying complicated problems into more familiar R^n problems.
Exactly! By understanding isomorphism, we can translate problems in one vector space to another, drastically simplifying our solutions.
Applications of Isomorphism
Unlock Audio Lesson
To wrap our discussion, let’s discuss real-world applications. Isomorphisms are crucial in areas like computer graphics, where transformations and dimensionality are fundamental. Can you think of other fields where this concept might apply?
I think it’s important in physics and engineering where understanding the behavior of systems in different contexts is essential.
Yes, especially in areas like structural analysis!
Absolutely! Vector space isomorphism helps in translating models from theoretical physics to applied engineering effectively, ensuring accuracy and understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore vector space isomorphism, defined as a bijective linear map between two vector spaces, indicating that they share structural properties. It highlights the fundamental concept that if two vector spaces have the same dimensions, they are isomorphic.
Detailed
Vector Space Isomorphism
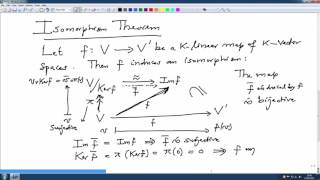
Vector space isomorphism is a critical concept in linear algebra that tells us when two vector spaces can be considered structurally identical. Specifically, two vector spaces, V and W, are said to be isomorphic if there exists a bijective linear map T: V → W such that:
T(av + bw) = aT(v) + bT(w) for all vectors v, w in V and all scalars a, b in the field F over which the vector spaces are defined.
This property implies that isomorphic vector spaces can be transformed into each other without losing any structural information about their linear properties. Additionally, when these spaces have equal dimensions, denoted as dimV = dimW = n, they can be viewed as isomorphic to R^n, strengthening the idea that dimensions serve as a bridge between different vector spaces. Thus, understanding vector space isomorphism is essential for deeper insights into linear transformations and their applications in various fields, including engineering, physics, and computer science.
Youtube Videos
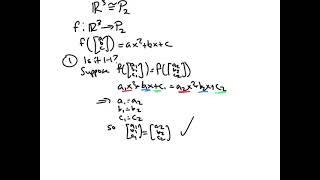
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Isomorphism
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Two vector spaces V and W over the same field are isomorphic if there exists a bijective linear map (isomorphism) T:V →W such that:
T(av+bw)=aT(v)+bT(w)
for all v,w∈V and a,b∈R.
Detailed Explanation
In this chunk, we define what it means for two vector spaces to be isomorphic. An isomorphism is a special type of function or mapping (denoted as T) that applies to elements of vector space V and corresponds them to elements in another vector space W. The key features of an isomorphism are that it must be both bijective (meaning every element in W is paired with exactly one element in V and vice versa) and linear. The equation shows that for any two vectors in V, when combined with scalar coefficients (a and b), the image of their linear combination under the map T is the same as the linear combination of their images, preserving the structure of the vector space.
Examples & Analogies
Think of an isomorphism like a perfect translation between two languages. For example, if you have a phrase in English, an isomorphism allows you to translate it perfectly into Spanish, maintaining the exact structure and meaning. Just as every English phrase corresponds to exactly one Spanish phrase, in an isomorphic relationship, every vector in one space corresponds to precisely one vector in another.
Significance of Isomorphism
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Significance:
- Isomorphic vector spaces are structurally identical.
- If dimV=dimW=n, then V ≅Rn.
Detailed Explanation
This chunk highlights the importance of isomorphism in understanding vector spaces. When two vector spaces are isomorphic, it means they share the same structure, which allows us to apply concepts from one space directly to the other. The notation 'V ≅ Rn' signifies that if both V and W have the same dimension (n), they can be viewed as identical in terms of their properties, although they may contain different elements. This is crucial for simplifying problems in linear algebra, as it allows us to work in a more familiar space Rn while solving problems originally framed in the context of V or W.
Examples & Analogies
Consider two different cities that are arranged in exactly the same way but have different buildings and names. For instance, if City A and City B both have a park, school, and shopping center, arranged in the same layout, they are structurally identical. You could take a map from City A and successfully apply it to City B without needing to change the layout, showcasing the principle of isomorphism in a geographical context.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Space Isomorphism: A bijective linear map that signifies structural equivalence between vector spaces.
-
Bijective Linear Map: A function that ensures a one-to-one correspondence between every element in two spaces.
-
Dimension Equivalence: The implication that if two vector spaces are isomorphic, they share the same dimensional properties.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider two vector spaces, V and W, defined over the same field. If T: V → W is a bijective linear map that respects the vector operations, then V and W are classified as isomorphic.
-
For instance, both R² and the set of linear polynomials can be shown to be isomorphic since they share the same dimension.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Isomorphism brings you and me, two spaces linked with symmetry.
📖 Fascinating Stories
-
Imagine two planets in the same galaxy that can transform into one another. They both have unique landscapes (vector spaces) but share similarities in their terrain (structure) allowing any traveler (vector) to find their way effortlessly.
🧠 Other Memory Gems
-
B.I.G. - Bijective, Identity, Correspondence: All key to understanding isomorphism.
🎯 Super Acronyms
I.S.O. - Isomorphic Spaces Offer
- Dimensional equivalence and structural identity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Isomorphism
Definition:
A bijective linear map between two vector spaces that indicates a structural similarity.
-
Term: Bijective
Definition:
A function that is both injective (one-to-one) and surjective (onto), establishing a one-to-one correspondence.
-
Term: Dimension
Definition:
The number of vectors in a basis of a vector space, indicating its structural size.