Dynamic Equation of Motion (EoM)
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dynamic Equations of Motion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we’ll discuss the dynamic equations of motion for robots. Can anyone give me a quick overview of what we mean by dynamic equations?

Are they the equations that show how robots move based on forces and torques?

Exactly! They help us understand how forces, including gravity and torques, cause robots to accelerate and move. The general form is M(q)q¨ + C(q, q˙)q˙ + G(q) = τ. Let's break this down.

What do M(q), C(q, q˙), and G(q) refer to?

Great question! M(q) is the mass or inertia matrix. C(q, q˙) captures Coriolis effects, and G(q) accounts for gravitational torques. Remember the acronym 'MCG'; it stands for Mass, Coriolis, Gravity!

So, M(q) represents the mass of the robot? How does that change with movement?

Yes, M(q) is dependent on the robot's configuration. As the robot moves, the positions of its mass can change, affecting the inertia. This crucial aspect is essential for calculating accurate motions.
Components of the Dynamic Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss each term in the dynamic equations in greater detail. Who can explain what the Mass matrix means?

Isn’t it just a way to represent the mass distribution of the robot?

Correct! The mass matrix M(q) is symmetric and positive definite. It's essential for representing how mass influences motion. Next, what about C(q, q˙)?

It represents the Coriolis and centrifugal forces, right? But how do they matter in robotics?

Absolutely! C(q, q˙) lets us compute the dynamical interactions in multi-DOF systems. These interactions can lead to non-linear effects, so we must account for them during motion planning and control.

And G(q) is just for gravity, right?

Yes! G(q) models how gravity affects each joint specifically, ensuring that we can gauge all positional effects when a robot is in motion.
Real-World Applications of Dynamic Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s wrap up by discussing how these dynamic equations are used in real robotic systems. Can anyone suggest an application?

I think they might be used in simulations to predict how a robot moves under different circumstances.

Exactly right! In simulations, dynamic equations help us verify trajectories and motion predictions. What about control applications?

So, like using inverse dynamics to calculate the forces needed for movements?

Absolutely! Inverse dynamics calculations are critical for ensuring accurate control over the robot's movements. Remember, understanding both forward and inverse dynamics allows for better designs and applications in robotic systems!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The dynamic equations of motion (EoM) express how various factors like mass, Coriolis forces, and gravity interact to influence the motion of robotic systems. The section outlines the structure of the EoM, explaining the components that contribute to a robot's dynamics and setting a foundation for further exploration of forward and inverse dynamics.
Detailed
Dynamic Equation of Motion (EoM)
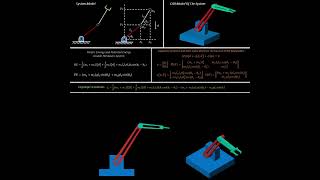
The dynamic equations of motion are crucial for understanding how robots interact with their environment through forces and torques. The general form of these equations in joint space is represented by:
$$ M(q)q¨ + C(q, q˙)q˙ + G(q) = τ $$
Where:
- M(q): Mass/Inertia matrix (n × n), incorporating the robot’s geometry and mass properties.
- C(q, q˙): Coriolis and centrifugal force matrix, which introduces non-linear interactions in multi-degree-of-freedom (DOF) systems.
- G(q): Gravity torque vector, modeling gravitational effects on each joint.
- τ: Vector of joint torques, indicating the forces applied.
- q, q˙, q¨: Vectors representing joint positions, velocities, and accelerations, respectively.
Components Explanation
- Mass Matrix M(q): A symmetric and positive definite matrix that is vital for defining the inertia of the robot based on its links.
- Coriolis/Centrifugal Matrix C(q, q˙): Accounts for complex interactions in systems with multiple degrees of freedom, affecting how torques are computed.
- Gravity Vector G(q): This term helps determine how gravity impacts robot joint movements, which is critical for stability and control.
Overall, understanding the EoM is fundamental for both forward and inverse dynamics, which are pivotal in robotics for control and simulation.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Form of Dynamic Equations
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The general form of robot dynamic equations (in joint space) is:
M(q)q¨+C(q,q˙)q˙ +G(q)=τ
Where:
• M(q): Mass/Inertia matrix (n × n)
• C(q,q˙): Coriolis and centrifugal force matrix
• G(q): Gravity torque vector
• τ: Vector of joint torques
• q,q˙,q¨: Joint position, velocity, and acceleration vectors
Detailed Explanation
The dynamic equation of motion for robots describes how the robot behaves under various forces and torques. This formula states that the sum of the forces acting on a robot, represented by the torque (τ), is equal to the combined effects of three main components:
1. Mass Matrix (M(q)): This matrix represents the robot's mass and how it changes depending on its configuration (positions of joints).
2. Coriolis and Centrifugal Forces (C(q, q˙)): This term accounts for the effects of rotation and changes in speed, which are important in multi-joint systems to ensure accurate motion prediction. It captures the non-linear interactions between joint velocities.
3. Gravity Torque Vector (G(q)): This vector accounts for the effects of gravity on the robot’s joints, ensuring the equations consider weight and stability.
Together, these components define how different variables like joint position (q), joint velocity (q˙), and joint acceleration (q¨) influence the overall motion of the robot.
Examples & Analogies
Think of the dynamic equations of motion as a recipe in a kitchen. Just like a recipe requires ingredients (in this case, M, C, and G) to create a dish (the robot's motion), these dynamic equations combine the forces acting on the robot to determine how it should move. If you change any ingredient in the recipe, the final dish (motion) will be different. For instance, if you add more flour (mass), it might affect how your cake rises (acceleration), just like changing a robot's mass can impact its motion.
Components Explanation
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Mass Matrix M(q): Symmetric and positive definite. Depends on link masses and geometry.
• Coriolis/Centrifugal Matrix C(q,q˙): Causes complex non-linear interactions in multi-DOF systems.
• Gravity Vector G(q): Models the effect of gravity on each joint.
Detailed Explanation
In this chunk, we break down each component of the dynamic equation:
1. Mass Matrix M(q): This matrix is crucial because it tells us how much 'weight' or 'inertia' each part of the robot has at different positions. It's symmetric, meaning its structure remains balanced, and it’s always positive, ensuring that our calculations remain valid. This matrix changes based on the robot's configuration, similar to how the layout of boxes might change whether they're stacked upright or lying down.
2. Coriolis/Centrifugal Matrix C(q, q˙): This matrix introduces complexity into our equations by accounting for the way joints affect each other in motion. In a multi-joint system, moving one joint can influence others due to their interconnected nature, leading to non-linear dynamics – for example, when driving a car, turning the steering wheel influences the direction of all the wheels, not just the front ones.
3. Gravity Vector G(q): This vector describes how gravity affects each joint of the robot. A robot on a slope will experience different gravitational effects than on level ground, resulting in variations in the torque needed to keep it stable.
Examples & Analogies
Imagine you are carrying multiple bags of groceries (mass matrix) that shift in weight as you move (Coriolis). If you start walking uphill, you will have to exert more effort to carry them all due to gravity pulling downwards (gravity vector). Each of these aspects needs to be considered for a successful shopping trip, just as engineers consider each matrix's impact when programming a robot.
Key Concepts
-
Dynamic Equations of Motion: The set of equations that governs the motion of robotic systems under the influence of forces and torques.
-
Mass/Inertia Matrix: Represents the distribution of mass in the robot, necessary for understanding how forces affect motion.
-
Coriolis Forces: Forces arising in rotating systems that are essential for accurate motion control in multi-DOF robots.
-
Gravity Effects: The influence of gravity on robot joints that must be modeled for precise motion prediction.
Examples & Applications
Using dynamic equations, engineers can simulate how a robotic arm responds to different joint torques in a virtual environment.
In a robotic manipulator, the mass matrix is calculated based on the dimensions and density of each link to ensure realistic simulations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Mass matrix here, keeps forces clear; Coriolis adds the twist, gravity's torque won't be missed.
Stories
Imagine a robot navigating a hilly landscape. The Mass Matrix helps it know its weight from various angles, the Coriolis effect gives it a helping hand to navigate turns, and each time it goes uphill or downhill, the Gravity Torque comes into play.
Memory Tools
Remember 'MCG' for Mass, Coriolis, and Gravity - the essential components of the dynamic equations.
Acronyms
MCG
Mass
Coriolis
Gravity – key terms for robot dynamics!
Flash Cards
Glossary
- Mass/Inertia Matrix
A matrix that describes the mass distribution and inertia properties of a robotic system, critical for calculating its motion dynamics.
- Coriolis and Centrifugal Matrix
A matrix that captures non-linear forces arising in multi-degree-of-freedom systems, affecting motion calculations.
- Gravity Torque Vector
A vector that models the torque produced by gravity on each joint of a robotic system.
- Joint Position
The current angle or position of a joint in the robot's kinematic chain.
- Joint Velocity
The rate of change of the joint position, indicating how fast the joint is moving.
- Joint Acceleration
The rate of change of the joint velocity, indicating how fast the joint's speed is increasing or decreasing.
Reference links
Supplementary resources to enhance your learning experience.
