Newton-Euler Formulation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Principles of Newton-Euler Formulation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're diving into the Newton-Euler formulation, a crucial approach in robot dynamics. Let's start with Newton's basic law: Force equals mass times acceleration. Can anyone explain what this means?

It means that the force acting on an object equals its mass multiplied by its acceleration.

Exactly! This principle helps us calculate how much force is needed to move a robot. Now, who can describe what Euler's law states?

Euler's law is related to rotational motion, right? It involves torque, inertia, and angular acceleration.

That's right! Remember, torque is what causes rotation, similar to how force causes linear motion. Let's summarize: we have linear dynamics via Newton's law and rotational dynamics via Euler's law.
Recursive Newton-Euler Algorithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the Recursive Newton-Euler Algorithm. It has two main phases. Who can tell me what these phases are?

I think the first phase is forward recursion, where we compute the velocities and accelerations?

Correct! That phase calculates the linear and angular velocities and accelerations from the base of the manipulator to the end-effector. What follows this phase?

Then we have backward recursion, where we work backwards to calculate forces and torques!

Excellent! This two-step approach optimizes our calculations, making the algorithm efficient for real-time control applications.
Advantages of the Newton-Euler Algorithm
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What do you think are the advantages of using the recursive Newton-Euler algorithm in robotics?

I believe it's because it's computationally efficient?

Yes! Its computational efficiency is crucial for real-time applications where quick responses are needed. Can anyone mention another application where this may be useful?

Motion planning in robots? It helps ensure safety and efficiency.

Absolutely! When you understand the dynamics, it enhances the precision and safety of robotic operations. Let’s conclude by examining how crucial understanding these dynamics is for effective robot control.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section details the Newton-Euler formulation, which integrates Newton’s second law of motion for translational dynamics and Euler’s equations for rotational dynamics. Key principles include the recursive Newton-Euler algorithm, its computational efficiencies, and its significance in robot dynamics, particularly for real-time control applications.
Detailed
Detailed Summary
The Newton-Euler formulation is foundational to understanding the dynamics of robotic systems. By merging Newton's second law, which relates force to mass and acceleration, with Euler's equations for rotation, it provides a comprehensive approach to analyze both translational and rotational motions of robots.
Key Concepts:
- Basic Principles: The two critical equations in the formulation are:
- Newton's Law: F = m · a, where F represents the force vector, m is mass, and a is linear acceleration.
- Euler's Law: τ = I · α + ω × (I · ω), covering rotational dynamics with τ as torque, I as inertia tensor, ω as angular velocity, and α as angular acceleration.
- Recursive Newton-Euler Algorithm: This two-phase algorithm is vital for n-link manipulators. It consists of:
- Forward Recursion: This phase calculates linear and angular velocities and accelerations from the base of the manipulator to the end-effector.
- Backward Recursion: This phase computes the forces and torques required at each joint, going from the end-effector back to the base, leading to efficient calculations.
- Advantages: The recursive Newton-Euler algorithm is known for its computational efficiency and suitability for real-time control applications, making it excellent for serial manipulators. This efficiency helps in applications like motion planning and adaptive control strategies.
The Newton-Euler formulation is essential in robotics for creating dynamic models that predict how robots behave in various conditions and operational scenarios. This understanding enhances the design and control of robots for tasks ranging from industrial applications to service robotics.
Youtube Videos




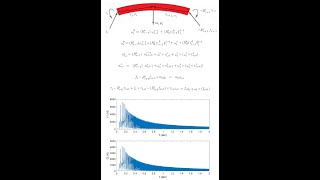



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Principles of Newton-Euler Formulation
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Newton-Euler formulation combines Newton's second law (for translational motion) and Euler's equations (for rotational motion).
- Newton's Law: F=m·a
- Euler's Law: τ =I·α+ω×(I·ω)
Where:
- F: Force vector
- m: Mass
- a: Linear acceleration
- τ: Torque
- I: Inertia tensor
- ω: Angular velocity
- α: Angular acceleration
Detailed Explanation
The Newton-Euler formulation is a critical concept in dynamics, specifically for understanding how forces and torques create movement in robotic systems. Newton's second law states that the force acting on an object is equal to its mass multiplied by its acceleration (F=m·a), implying that the greater the mass, the more force is required to accelerate it. On the rotational side, Euler's equations relate torque to angular acceleration along with the angular velocity and inertia tensor, highlighting how rotation is also influenced by mass distribution and speed. Together, these principles allow us to derive the equations of motion for robots, showing how linear and rotational motions are interconnected.
Examples & Analogies
Imagine pushing a shopping cart. The more items you add (increased mass), the harder you must push to make it accelerate. This scenario correlates with Newton's law (F=m·a). Now, think of trying to spin a heavy merry-go-round. The force you apply (torque) will determine how quickly it spins, and the mass distribution will affect how responsive it is to your push. These principles are fundamental when programming robots to move and respond effectively.
Recursive Newton-Euler Algorithm
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For an n-link manipulator, the recursive Newton-Euler algorithm operates in two phases:
1. Forward recursion: Compute linear and angular velocities and accelerations from base to end-effector.
2. Backward recursion: Compute forces and torques from end-effector to base.
Detailed Explanation
The recursive Newton-Euler algorithm is a systematic method used to analyze complex robotic systems with multiple links (joints). It performs calculations in two major steps. First, in the forward recursion phase, the algorithm determines the velocities and accelerations of each link starting from the base (the stationary part of the robot) extending to the end-effector (the part of the robot that interacts with the environment). This establishes how fast and in what direction each segment of the robot is moving. Secondly, in the backward recursion phase, the algorithm calculates the forces and torques that act on each link, starting from the end-effector back to the base, thus allowing for the determination of how much force each joint motor needs to exert to achieve the intended movement.
Examples & Analogies
Think of a puppet controlled by strings. As you pull on a string attached to the hand (forward recursion), you observe how the entire puppet’s body shifts in response. Now, consider what you need to do at the puppet's shoulder (backward recursion) to make that hand move effectively. This two-way communication is akin to how the recursive algorithm calculates motion and forces in robotic arms, ensuring every part moves in harmony.
Advantages of the Newton-Euler Formulation
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
• Computationally efficient
• Suitable for real-time control applications
• Good for serial manipulators
Detailed Explanation
The Newton-Euler formulation offers several advantages for robotics, making it particularly valuable in dynamic control applications. First, it is computationally efficient, meaning it can perform calculations quickly, which is crucial for real-time systems that require immediate responses, like robotic arms that must react to their environment or user input without lag. Second, it is well-suited for real-time control applications because it continuously updates motion calculations based on the current state of the system. Finally, the formulation excels with serial manipulators, where each joint is aligned in a single chain, allowing for easier calculations as each component's motion can be independently analyzed and linked together.
Examples & Analogies
Imagine a video game character that needs to respond to player commands instantly; the faster the game can compute the character's movements, the smoother the gameplay feels. In robotics, similarly, using efficient algorithms like Newton-Euler allows robots to execute complex actions quickly and accurately, ensuring they perform tasks seamlessly, whether it's assembling products or assisting in surgeries.
Key Concepts
-
Basic Principles: The two critical equations in the formulation are:
-
Newton's Law: F = m · a, where F represents the force vector, m is mass, and a is linear acceleration.
-
Euler's Law: τ = I · α + ω × (I · ω), covering rotational dynamics with τ as torque, I as inertia tensor, ω as angular velocity, and α as angular acceleration.
-
Recursive Newton-Euler Algorithm: This two-phase algorithm is vital for n-link manipulators. It consists of:
-
Forward Recursion: This phase calculates linear and angular velocities and accelerations from the base of the manipulator to the end-effector.
-
Backward Recursion: This phase computes the forces and torques required at each joint, going from the end-effector back to the base, leading to efficient calculations.
-
Advantages: The recursive Newton-Euler algorithm is known for its computational efficiency and suitability for real-time control applications, making it excellent for serial manipulators. This efficiency helps in applications like motion planning and adaptive control strategies.
-
The Newton-Euler formulation is essential in robotics for creating dynamic models that predict how robots behave in various conditions and operational scenarios. This understanding enhances the design and control of robots for tasks ranging from industrial applications to service robotics.
Examples & Applications
Example of applying Newton's law to a robotic arm lifting an object, calculating the required force based on the mass and desired acceleration.
Demonstrating Euler’s law by analyzing a rotating robotic joint where torque calculations are essential for control.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When mass and speed combine, force is what you find.
Stories
Imagine a robot arm lifting weights; it needs the right amount of force to succeed. Newton's law helps it know exactly how much it needs to lift.
Memory Tools
NEM: Newton's Law, Euler's Law, and the Recursive Algorithm.
Acronyms
FORCE
= mass x acceleration is Newton's main equation.
Flash Cards
Glossary
- Newton's Law
A principle stating that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
- Euler's Law
An equation relating torque, angular acceleration, and angular velocity, critical for understanding rotational motion.
- Torque
A measure of the force that can cause an object to rotate about an axis.
- Inertia Tensor
A mathematical representation of the distribution of mass in a body, affecting its rotational dynamics.
- Recursive Algorithm
An algorithm that solves a problem by breaking it down into smaller subproblems of the same type.
Reference links
Supplementary resources to enhance your learning experience.
