Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Boolean Minimization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing Boolean minimization algorithms and why they're vital in logic synthesis. Can anyone tell me what Boolean minimization aims to achieve?
It aims to simplify Boolean expressions to make the logic circuits more efficient.
Correct! By simplifying, we reduce the area and delay of circuits. Let's dive deeper into the first algorithm: the QuineβMcCluskey. What do you think makes this algorithm distinctive?
Isnβt it exhaustive? It looks through all possibilities to eliminate terms.
Exactly! Remember, exhaustive methods can be effective for smaller Boolean functions but may not scale well. Can anyone suggest where we might apply this algorithm?
It might be useful in small-scale integrated circuits!
Good point! So, we can use Quine-McCluskey for those smaller designs.
Karnaugh Maps
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, letβs talk about Karnaugh Maps, or K-Maps. Who can explain what they are?
K-Maps are visual tools used to simplify Boolean expressions by grouping ones together!
Awesome! What are the limitations of K-Maps?
They work best for up to four variables, right? Larger functions can get complicated.
Exactly! When we move beyond four variables, managing the visual representation becomes challenging. Thatβs where automated tools come in, like the Espresso Algorithm. What do you know about Espresso?
I think itβs designed to be faster and more efficient than Quine-McCluskey.
Right again! It uses heuristics to find minimum expressions quickly. Keep this in mind for practical applications.
Espresso Algorithm and BDDs
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs explore the Espresso Algorithm further. How does it improve on the previous methods?
It uses heuristic steps instead of an exhaustive search, right?
Exactly! This makes it suitable for larger functions. Can anyone explain how BDDs fit into this picture?
Binary Decision Diagrams represent Boolean functions as graphs, which makes it easier to simplify and manipulate them.
Right! BDDs allow for efficient optimization on a larger scale. Remember, their structure can lead to compact representations of Boolean functions.
So, in summary, these algorithms are crucial for different sizes and complexities of Boolean expressions.
Absolutely! Each algorithm serves a particular niche in Boolean minimization, facilitating more efficient circuit design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
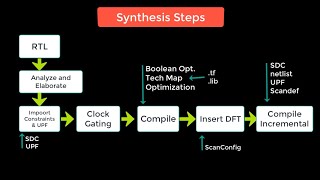
This section covers essential Boolean minimization algorithms such as QuineβMcCluskey, Karnaugh Maps, Espresso Algorithm, and Binary Decision Diagrams. These techniques play a significant role in simplifying Boolean functions, ultimately leading to optimized area and performance in VLSI circuits.
Detailed
Boolean Minimization Algorithms
Boolean minimization is pivotal in logic synthesis, aimed at simplifying Boolean expressions to enhance circuit performance and reduce area. This section introduces key algorithms used in Boolean minimization:
- QuineβMcCluskey Algorithm: An exhaustive algorithm that eliminates terms from Boolean expressions through systematic pairing based on variable differences. It's effective for small Boolean functions.
- Karnaugh Maps (K-Maps): A visual technique allowing for the simplification of Boolean expressions by grouping terms intuitively, ideal for expressions with up to four variables.
- Espresso Algorithm: A heuristic-based algorithm that provides greater efficiency over QuineβMcCluskey, widely adopted in practical synthesis tools for minimizing Boolean expressions.
- Binary Decision Diagrams (BDD): A graphical representation of Boolean functions as directed acyclic graphs, enabling efficient manipulation and optimization.
These algorithms are crucial for reducing the complexity of Boolean functions, streamlining the design process and improving resultant circuit performance.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Importance of Boolean Minimization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Boolean minimization plays a critical role in logic synthesis. It involves reducing the complexity of Boolean expressions, which can help reduce the area and delay of the resulting circuits.
Detailed Explanation
Boolean minimization is essential in logic synthesis because it simplifies Boolean expressions. When we reduce the complexity of these expressions, we can create digital circuits that occupy less physical space (area) and operate faster (delay). This means our designs are more efficient and cost-effective.
Examples & Analogies
Think of it like decluttering your room. By reducing the number of items and organizing what's left, you create a more spacious and comfortable environment. Similarly, Boolean minimization clears out unnecessary complexities in circuit design, leading to more efficient digital systems.
QuineβMcCluskey Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
QuineβMcCluskey Algorithm: This is an exhaustive approach that systematically eliminates terms from a Boolean expression by combining pairs of terms that differ in only one variable. Itβs widely used for minimization of small Boolean functions.
Detailed Explanation
The QuineβMcCluskey Algorithm is a method used to simplify Boolean expressions systematically. It works by identifying pairs of terms that can be combined, making the expression simpler. This algorithm is particularly useful for small Boolean functions and ensures that you explore all possible ways to simplify the expression exhaustively.
Examples & Analogies
Imagine solving a jigsaw puzzle where you systematically merge pieces that fit together. Each time you identify two pieces that connect, you create a more complete picture. Similarly, the QuineβMcCluskey Algorithm connects pairs of terms in Boolean expressions, leading to a clearer, simpler function.
Karnaugh Maps (K-Maps)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
K-Maps are used for simplifying Boolean expressions by visually grouping terms that can be combined. This is especially useful for simplifying expressions with up to four variables, where visual grouping is intuitive.
Detailed Explanation
Karnaugh Maps (K-Maps) are a visual tool used to simplify Boolean expressions. They allow designers to group together adjacent terms that can be combined, which simplifies the expression. K-Maps are particularly effective for functions with up to four variables, where the visual layout makes it easier to see how terms can be combined.
Examples & Analogies
Think of a K-Map like a seating chart for a dinner party. If you group together people who get along well, the overall atmosphere of the party improves. Similarly, K-Maps help group terms in a Boolean expression to create a simpler and more efficient logical function.
Espresso Algorithm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Espresso is a more efficient algorithm than the QuineβMcCluskey approach, widely used in practical synthesis tools. It performs minimization through a series of heuristic steps to reduce Boolean expressions to their simplest form.
Detailed Explanation
The Espresso Algorithm is an optimization method that improves on the QuineβMcCluskey Algorithm by using heuristic techniques. This means it employs rules of thumb to quickly find simplified forms of Boolean expressions without exhaustively analyzing every possibility. This efficiency makes it a popular choice in practical applications, particularly in software tools for logic synthesis.
Examples & Analogies
Consider the Espresso Algorithm like a talented chef who quickly prepares a delicious meal using efficient cooking techniques, rather than a novice who painstakingly follows every recipe detail. The chef knows shortcuts and smart substitutions that streamline the cooking process, leading to quicker, high-quality results.
Binary Decision Diagrams (BDD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
BDDs represent Boolean functions as directed acyclic graphs, which make it easier to manipulate and optimize the Boolean functions. BDD-based algorithms are efficient and can be used for large-scale optimizations.
Detailed Explanation
Binary Decision Diagrams (BDDs) are a method of representing Boolean functions as graphs. These directed acyclic graphs help simplify the manipulation and optimization of complex Boolean functions. BDDs can handle larger expressions efficiently, making them suitable for applications requiring extensive logic optimization.
Examples & Analogies
Think of BDDs like a mind map that visually organizes complex ideas and relationships. Just as a mind map can simplify a complicated subject by breaking it down into interconnected parts, BDDs break down complex Boolean functions into manageable graph structures that reveal their optimizable features.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Boolean Minimization: The process of reducing the complexity of Boolean expressions to optimize circuit performance.
-
QuineβMcCluskey Algorithm: An exhaustive method for simplifying Boolean expressions.
-
Karnaugh Maps: A visual method for simplifying Boolean functions for up to four variables.
-
Espresso Algorithm: A heuristic approach for efficient Boolean minimization.
-
Binary Decision Diagrams (BDD): A data structure that represents Boolean functions, facilitating large-scale optimization.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using a K-Map to simplify the expression A'B + AB' + AB leads to the simplified form A + B.
-
Applying the QuineβMcCluskey Algorithm on a Boolean expression with multiple minterms helps in systematically reducing it to fewer terms.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
For simplifying logic, don't lose the plot, use Quine-McCluskey to give it a shot!
π Fascinating Stories
-
Imagine a gardener (Espresso) who quickly prunes the overgrown bushes (Boolean functions), making them neat and tidy for efficient growth (circuit performance).
π§ Other Memory Gems
-
Remember QKEB - Quine-McCluskey, Karnaugh, Espresso, Binary (Decision Diagrams) for Boolean minimization!
π― Super Acronyms
KISS
- Keep It Simple with K-Maps for small scopes!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: QuineβMcCluskey Algorithm
Definition:
An exhaustive method for simplifying Boolean functions by systematically eliminating terms that differ by one variable.
-
Term: Karnaugh Maps
Definition:
A graphical tool used for simplifying Boolean expressions by visually grouping together adjacent cells representing minterms.
-
Term: Espresso Algorithm
Definition:
A heuristic algorithm that simplifies Boolean functions efficiently through a series of reduction steps.
-
Term: Binary Decision Diagrams (BDD)
Definition:
A data structure that represents Boolean functions as directed acyclic graphs, allowing efficient manipulation.