Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Sign Conventions
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we are going to discuss the New Cartesian Sign Convention used in optics, specifically for spherical mirrors. Can anyone tell me what a convention is?
I think a convention is a standard way of doing something.
Exactly! It provides a common framework. In our case, it helps us to consistently understand where the object is placed relative to the mirror.
So, the object is always to the left of the mirror, right?
Correct! When we place the object to the left, the light from the object falls on the mirror from that side. This is essential while applying the equations.
Understanding Distance Measurements
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's talk about how to measure distances. All distances parallel to the principal axis are measured from the pole. Who can tell me how we define positive and negative directions?
Distances to the right of the pole are positive, and those to the left are negative.
That's right! Positive distances go in the +x direction while negative distances move towards -x. Good job!
What about distances above or below the principal axis?
Excellent question! Distances measured above the axis are positive (+y), and below are negative (−y). Remember this as it will be applied frequently.
Importance of Sign Convention
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, why do you think this sign convention is important for us?
It helps us keep track of the directions when we do calculations.
And it prevents confusion when looking at different positions of the object and image.
Exactly! By following these conventions, we can easily apply the mirror formula and solve problems.
What is the mirror formula?
The mirror formula relates the object distance (u), image distance (v), and focal length (f): 1/f = 1/v + 1/u. It’s crucial that we use the proper signs when substituting values.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the New Cartesian Sign Convention for spherical mirrors is discussed, describing how distances like object distance, image distance, and focal lengths are measured. The pole of the mirror is the origin, and specific rules about measuring distances to the left or right of the pole are highlighted.
Detailed
Detailed Summary
In the study of light and its behavior during reflection by spherical mirrors, it is essential to adhere to a systematic method of assigning signs to the various distances involved. This approach is guided by the New Cartesian Sign Convention, which establishes a clear framework for representing measurements in optics.
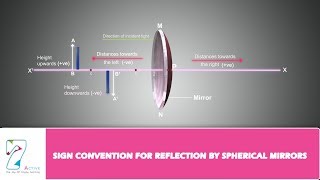
- Origin Setting: The pole (P) of the mirror is taken as the origin of the coordinate system. This is critical for interpreting various optical phenomena correctly.
- Object Positioning: The convention stipulates that the object is always positioned to the left of the mirror. This arrangement implies that light from the object approaches from the left-hand side of the mirror.
- Distance Measurement: All distances parallel to the principal axis are measured from the pole:
- Distances measured to the right of the pole are positive (+x).
- Distances measured to the left of the pole are negative (−x).
- Perpendicular Distances: Distances measured perpendicular to the principal axis are also defined:
- Distances above the principal axis are considered positive (+y).
- Distances below the principal axis are negative (−y).
This clear demarcation aids in the consistent application of the mirror formula and facilitates solving various numerical problems related to spherical mirrors.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Sign Convention
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
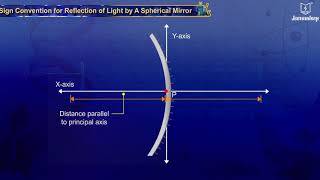
While dealing with the reflection of light by spherical mirrors, we shall follow a set of sign conventions called the New Cartesian Sign Convention. In this convention, the pole (P) of the mirror is taken as the origin. The principal axis of the mirror is taken as the x-axis (X’X) of the coordinate system.
Detailed Explanation
The New Cartesian Sign Convention is a method used to simplify the calculations involving reflection in spherical mirrors. In this system, the pole of the mirror (the point where the light rays strike the mirror) is set as the reference point or origin. The vertical line that goes through the center of the mirror is defined as the x-axis. This standardizes how we measure distances and helps avoid errors in calculations.
Examples & Analogies
Think of using a map where you have set a specific point as your 'home'—all distances from your home can be measured either positively (to the right) or negatively (to the left). Similarly, the pole of the mirror acts as that reference point for measuring distances in the sign convention.
Object Placement and Distance Conventions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- The object is always placed to the left of the mirror. This implies that the light from the object falls on the mirror from the left-hand side.
- All distances parallel to the principal axis are measured from the pole of the mirror.
Detailed Explanation
In this convention, we always assume that the object is on the left side of the mirror, meaning rays of light travel from the left towards the mirror. This positioning helps us organize our reflections and provides consistency in the calculations. Additionally, distances that we measure along the principal axis (x-axis) start from the pole of the mirror, allowing us to define positive and negative distances depending on their direction.
Examples & Analogies
Imagine shining a flashlight towards a wall. The source of the light (the flashlight) is your object. In our sign convention, we always keep the flashlight on the left side when considering where the light goes. Any measurements we make about the position or distance to the wall (the mirror in this case) start from the place where the light beam first hits, just like we measure distances from the pole of the mirror.
Positive and Negative Distances
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- All the distances measured to the right of the origin (along + x-axis) are taken as positive while those measured to the left of the origin (along – x-axis) are taken as negative.
- Distances measured perpendicular to and above the principal axis (along + y-axis) are taken as positive.
- Distances measured perpendicular to and below the principal axis (along – y-axis) are taken as negative.
Detailed Explanation
In this section of the convention, we define how to classify different distances based on their direction. Distances moving to the right (away from the mirror) are considered positive, while distances to the left (towards the mirror) are negative. Similarly, vertical measurements above the principal axis are positive, and those below are negative. This system allows us to easily describe the location of objects and images related to the mirror during calculations.
Examples & Analogies
Think of a number line that you learned in math class. When you move to the right, the numbers increase and are considered positive; when you move to the left, the numbers decrease and are considered negative. Similarly, in our mirror convention, anything to the right of the pole is positive, while everything to the left is negative, helping us keep track of where things are located relative to the mirror.
Visual Representation of the Sign Convention
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The New Cartesian Sign Convention described above is illustrated in figure 9.9 for your reference. These sign conventions are applied to obtain the mirror formula and solve related numerical problems.
Detailed Explanation
Figure 9.9 visually represents how we set our coordinate system in relation to the mirror. It shows the directions for positive and negative distances clearly, which helps in understanding and applying the sign support the calculations related to mirrors. Understanding this visual representation ensures that students can apply the correct principles when using mathematical equations in mirror problems.
Examples & Analogies
Just as you'd refer to a map that shows you where everything is located—like where the streets are and where your destination is—the visual representation of the sign convention provides a clear guide for understanding how to measure and calculate distances in relation to the mirror, making it easier to navigate through problems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Sign Convention: A systematic approach to assigning signs to the image, object, and focal lengths in spherical mirrors.
-
Positive/Negative Distances: Rules for measuring distances in the Cartesian plane related to mirror positioning.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When calculating the location of images formed by mirrors, knowing that distances to the left are negative assists in ensuring correct calculations.
-
Using the mirror formula requires proper signs; for instance, if the object distance is -30 cm, and the image distance is +60 cm, inserting these values correctly will yield correct results.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To measure distances nice and neat, pole to left makes negative sweet.
📖 Fascinating Stories
-
Imagine standing in front of a mirror: if you put an object to the left, the light journey begins from that side, always and forever.
🧠 Other Memory Gems
-
P For Pole, F for Focus; as you measure y and x, keep these points with you next.
🎯 Super Acronyms
O for Object, I for Image, F for Focus—remember these when you measure!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Pole (P)
Definition:
The central point of a spherical mirror where measurements begin.
-
Term: Principal axis
Definition:
The straight line that passes through the pole and the center of curvature of the mirror.
-
Term: Object distance (u)
Definition:
The distance from the object to the pole of the mirror.
-
Term: Image distance (v)
Definition:
The distance from the image formed to the pole of the mirror.
-
Term: Focal length (f)
Definition:
The distance from the pole to the principal focus of the mirror.