Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Refractive Index
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we’re going to discuss the refractive index. Can anyone tell me what they think it means?
I think it’s something to do with how light travels in different materials.
Exactly! The refractive index tells us how much light bends when it passes from one medium to another. It’s calculated as the ratio of the speed of light in vacuum to the speed of light in the medium.
So, what’s the formula?
"The formula for refractive index
Optical Density vs. Mass Density
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s discuss optical density. Who can define what that means?
Is it the same as mass density?
Not exactly! Optical density is more about how light interacts with a substance, while mass density refers to its mass per unit volume. For example, kerosene has a higher refractive index than water, which can be confusing since its mass density is lower.
So, does that mean the light behaves differently in kerosene compared to water?
Exactly! Light travels faster in water than in kerosene due to the difference in refractive indices. So the refractive index can help us determine how light will behave in each material.
What about everyday examples of these effects?
Great point! When you see a straw in a glass of water that looks bent, that’s refraction due to the different speeds of light in air and water. This bending is a direct result of the refractive index.
To recap, optical density and mass density measure different interactions of light and matter.
Calculating the Refractive Index
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s move to calculating the refractive index. If light in a medium travels at a speed of 2.25 × 10^8 m/s, what’s the refractive index compared to light in a vacuum?
Well, the speed of light in a vacuum is 3 × 10^8 m/s, right?
Correct! Now, can you calculate it?
So, n = 3 × 10^8 / 2.25 × 10^8 = 1.333.
Exactly! This tells us that light slows down when it enters this medium. What implications does that have?
It means the medium bends light towards itself?
Yes! And that bending direction has real-world applications, such as in fiber optics or lenses.
So, always remember, calculating refractive indices helps predict how light will behave when it encounters different materials.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains the concept of refractive index, how it relates to the speed of light in different media, and its significance in understanding light behavior during refraction. It introduces the formulas for refractive index and connects it to concepts like optical density.
Detailed
The Refractive Index
The refractive index (
n
) is a dimensionless number that describes how light propagates through a material. It is defined as the ratio of the speed of light in a vacuum (
v
1) to the speed of light in the medium (
v
2):
n_2 =
v_1/v_2.
Light travels fastest in a vacuum, at about 3 × 10^8 m/s. When light enters a medium such as glass or water, it slows down, leading to bending of the light rays, which is known as refraction. The refractive index (
n
) indicates how optically dense a medium is: the higher the refractive index, the denser the medium. Notably, refractive index is not solely about mass density; sometimes a medium can be optically denser even if it has a lower mass density than another medium. The concepts of optical density, the relationship between speed of light in different media, and the mathematical representations of refractive indices are critical in studying optics and understanding phenomena such as light bending at the boundaries between different substances.
Youtube Videos
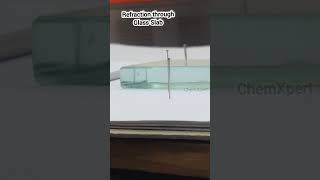
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Refractive Index
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You have already studied that a ray of light that travels obliquely from one transparent medium into another will change its direction in the second medium. The extent of the change in direction that takes place in a given pair of media may be expressed in terms of the refractive index, the “constant” appearing on the right-hand side of Eq.(9.4).
Detailed Explanation
When light travels from one medium to another at an angle, it does not continue on the same path. Instead, it bends, changing its direction. This bending can be quantitatively described by a number known as the refractive index. Essentially, the refractive index tells us how much the light will bend when it enters a new medium.
Examples & Analogies
Think about how a straw looks when placed in a glass of water. The part of the straw in the water appears broken or bent at the water's surface due to refraction. The refractive index helps to quantify this bending in different materials.
Connection to Light Speed
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The refractive index can be linked to an important physical quantity, the relative speed of propagation of light in different media. It turns out that light propagates with different speeds in different media. Light travels fastest in vacuum with speed of 3×10^8 m s–1. In air, the speed of light is only marginally less, compared to that in vacuum. It reduces considerably in glass or water.
Detailed Explanation
Light travels at varying speeds in different environments. In a vacuum, it moves at its highest speed, which is approximately 300,000 kilometers per second. When light enters materials like air, water, or glass, its speed decreases. The refractive index of a medium is a measure of this reduction in speed. The greater the refractive index, the slower the light travels in that medium.
Examples & Analogies
Imagine driving a car on different types of roads. On a smooth highway (like a vacuum), you can drive fast. However, on a gravel road or through a city (like water or glass), your speed decreases significantly. This illustrates how the medium affects the speed of light.
Understanding Refractive Index Values
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The value of the refractive index for a given pair of media depends upon the speed of light in the two media, as given below. Consider a ray of light travelling from medium 1 into medium 2. Let v be the speed of light in medium 1 and v2 be the speed of light in medium 2. The refractive index of medium 2 with respect to medium 1 is given by the ratio of the speed of light in medium 1 and the speed of light in medium 2. This is usually represented by the symbol n.
Detailed Explanation
The refractive index (n) quantifies how light speeds differ between two media. It can be calculated using the formula: n = v1/v2, where v1 is the speed of light in the first medium and v2 in the second. If the refractive index is greater than 1, it means light is slower in this medium compared to the first medium.
Examples & Analogies
Consider pouring syrup into water. Syrup is denser and 'thicker,' causing light to scatter more than in clear water. Depending on the medium's density and consistency, light changes speed—this is quantified by the refractive index.
Absolute and Relative Refractive Index
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is called the absolute refractive index of the medium. It is simply represented as n2. If c is the speed of light in air and v is the speed of light in the medium, then, the refractive index of the medium n is given by n2 = c/v2.
Detailed Explanation
The absolute refractive index measures how light propagates in a medium compared to its speed in a vacuum. This is essential for understanding how much the light will bend when entering or exiting a medium, particularly regarding optics and lens design.
Examples & Analogies
Using a still lake reflects the sky’s colors while considering how the water's refractive index affects the light! When you look at a fish underwater, it may appear closer or farther than it actually is because of the refractive properties of water compared to air.
Optical vs Mass Density
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Note from Table 9.3 that an optically denser medium may not possess greater mass density. For example, kerosene having higher refractive index, is optically denser than water, although its mass density is less than water.
Detailed Explanation
Optical density can differ from mass density, which is about the weight of material in a given volume. A medium can be 'optically denser' with a higher refractive index, which means light travels slower through it, regardless of its mass. Kerosene, for instance, is less heavy than water but slows down light more, making it optically denser.
Examples & Analogies
Similar to how heavy rafts float on water but don’t slow down a boat speeding in a lake, some substances can appear light and fast but change how light behaves.
Light Speed and Bending of Rays
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The speed of light is higher in a rarer medium than a denser medium. Thus, a ray of light travelling from a rarer medium to a denser medium slows down and bends towards the normal. When it travels from a denser medium to a rarer medium, it speeds up and bends away from the normal.
Detailed Explanation
Understanding light's behavior as it transitions between media helps clarify why and how it bends—what we term 'snell's law.' Essentially, the transition fundamentally affects its direction due to differences in speed.
Examples & Analogies
Consider diving into a pool from the side: as you enter the water, you slow down, changing direction significantly. When you jump back into the air, you speed up and shift direction again—this mirrors how light reacts as it moves through different densities.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Refractive Index: The ratio of light's speed in a vacuum to its speed in a medium.
-
Optical Density: A medium's ability to refract light, not to be confused with mass density.
-
Light Speed Variations: Light travels at different speeds in different materials, affecting its direction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When viewing a straw in a glass of water, it appears to be bent due to refraction. This is a direct demonstration of the refractive index at work.
-
The refractive indices of various materials differ, with water having a refractive index of about 1.33.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To bend or break, light takes its cue, / Faster in air than in water, it's true.
📖 Fascinating Stories
-
Imagine a race between light in air and light in water; air wins because it’s free to roam while water slows it down!
🧠 Other Memory Gems
-
Use 'WETER' to remember: Water, Ether, and their Refractive indices.
🎯 Super Acronyms
‘RID’ for Remembering
- Refractive Index Determines light behavior.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Refractive Index
Definition:
A dimensionless number indicating how much light bends when entering a new medium.
-
Term: Optical Density
Definition:
A measure of how much a substance slows down light compared to a vacuum.
-
Term: Speed of Light
Definition:
The speed at which light travels in a vacuum, approximately 3 × 10^8 m/s.
-
Term: Medium
Definition:
Any substance through which light travels.