Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Electric Fields Outside the Shell
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to explore how a uniformly charged thin spherical shell influences the electric field around it. Can anyone tell me what they think happens to the electric field outside of this shell?
I think the field should be similar to how it is for a point charge at the center.
That's correct! The electric field outside the shell acts as if all of the shell's charge were concentrated at its center. We can express this mathematically using Gauss's law.
Can you remind us what Gauss's law states?
Sure! Gauss's law relates the electric flux through a closed surface to the charge enclosed by that surface. It's a crucial concept for our calculations. So if I have a Gaussian surface outside the shell, I can derive the formula for the electric field.
What would that formula look like?
The formula is E = q / (4ΟΞ΅βrΒ²), where 'q' is the total charge of the shell and 'r' is the distance from the center. Remember that 'E' points radially outward if 'q' is positive.
So, does this mean the electric field behaves just like a point charge would?
Exactly! Itβs a critical conclusion from this section. To summarize, when outside the shell, the electric field behaves as if all charge were at the center.
Electric Field Inside the Shell
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs discuss the electric field inside the spherical shell. Can anyone guess what happens there?
I would think it would be similar to the inside of a charged conductor, so maybe zero?
Great insight! You are correct. The electric field inside a uniformly charged thin shell is indeed zero. This can be attributed to the Gaussian surface we use.
How is that derived from Gauss's law?
When we choose a Gaussian surface inside the shell, we find that it encloses no charge. Thus, according to Gauss's law, the net electric flux must be zero, leading us to conclude that E = 0 for r < R.
So does that mean that moving around inside will feel like there's no electric field acting on me?
Exactly! Thatβs a significant and counterintuitive result when we consider electrostatics.
Thank you! That makes it clearer.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The electric field created by a uniformly charged thin spherical shell is evaluated using Gauss's law, revealing that it behaves as though the charge were placed at the center outside the shell, while the electric field inside the shell is zero. This summarises the critical points of electric field behavior and symmetry in electrostatics.
Detailed
Detailed Summary
In this section, we study the electric field generated by a uniformly charged thin spherical shell using Gauss's law. The spherical symmetry allows us to conclude that:
1. Outside the Shell: For a point located outside the shell (radius r, where r > R), the electric field can be represented as if all the shell's charge were concentrated at its center. Thus, using Gauss's law, the electric field (E) at any point outside the shell is given by:
E = \( \frac{q}{4\pi \epsilon_0 r^2} \)
where q is the total charge on the shell.
- Inside the Shell: For any point located inside the shell (r < R), it is determined that the electric field is zero. This can be derived from the fact that there are no charges enclosed by the Gaussian surface drawn within the shell. Hence:
E = 0 (for r < R)
Significance
Understanding fields around charged objects lays the groundwork for principles in electrostatics, impacting devices such as capacitors and influencing fields in physics and engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Field Outside the Shell
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
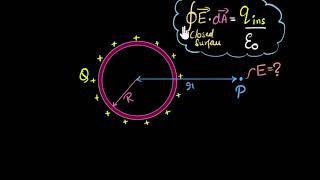
Consider a point P outside the shell with radius vector r. To calculate E at P, we take the Gaussian surface to be a sphere of radius r and with centre O, passing through P. All points on this sphere are equivalent relative to the given charged configuration. (That is what we mean by spherical symmetry.) The electric field at each point of the Gaussian surface, therefore, has the same magnitude E and is along the radius vector at each point. Thus, E and DS at every point are parallel and the flux through each element is E DS. Summing over all DS, the flux through the Gaussian surface is E Γ 4ΟrΒ². The charge enclosed is Ο Γ 4ΟRΒ². By Gaussβs law, E Γ 4ΟrΒ² = (Ο Γ 4ΟRΒ²) / Ξ΅β.
Detailed Explanation
To find the electric field E outside a uniformly charged thin spherical shell, we use Gauss's law, which relates the electric flux through a closed surface to the charge enclosed within it. We consider a point outside the shell and draw an imaginary spherical surface (our Gaussian surface) around the shell to apply Gauss's law. Since the shell is spherical and uniformly charged, the electric field at any point on this spherical surface is constant and directed radially outward. Therefore, the electric flux through the surface is simply the electric field E times the surface area of the sphere (E Γ 4ΟrΒ²). The charge enclosed by our Gaussian surface is the total charge on the sphere, which can be calculated from the surface charge density times the surface area of the shell. Setting these equal via Gauss's law gives us the formula for the electric field: E = (ΟRΒ²)/(Ξ΅βrΒ²). Thus, the electric field outside a uniformly charged shell mimics that of a point charge located at the center.
Examples & Analogies
Imagine standing in a large basketball arena filled with people carrying equal-sized balloons. If you are outside the arena and you hear a loud 'pop' from one of the balloons, the sound (representing the electric field) you hear from that one balloon is similar to the electric field you experience at position P outside the sphere. The impact of that one balloon's pop can be felt uniformly from a distance, just like how the field behaves outside the charged shell as if the charge were concentrated at the center.
Field Inside the Shell
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this case, the Gaussian surface encloses no charge. The flux through the Gaussian surface, calculated as before, is E Γ 4ΟrΒ². Gaussβs law then gives E Γ 4ΟrΒ² = 0, i.e., E = 0 (r < R) that is, the field due to a uniformly charged thin shell is zero at all points inside the shell.
Detailed Explanation
To find the electric field E inside a uniformly charged thin spherical shell, we again apply Gauss's law. In this scenario, we consider a Gaussian surface that lies entirely within the shell. The key here is that all the charge of the shell is located on its surface, and no charge exists within the volume of the shell itself. Consequently, when calculating the charge enclosed by our Gaussian surface, we find that it is zero. Gauss's law then tells us that the electric flux E Γ 4ΟrΒ² must also be zero, which leads us to conclude that E = 0 for any point inside the shell. This implies that there is no electric field within the hollow space of a charged shell, a fact that is fundamental in electrostatics.
Examples & Analogies
Think of being inside a large, empty room (the inside of the shell) that is perfectly insulated from outside sounds. Regardless of how much noise is made outside (the charge), you won't hear any sound (electric field) inside the room. The silence inside the room represents the electric field being zero at all locations within the shell.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Electric Field: The force per unit charge in an electric field around charged objects.
-
Gauss's Law: The electric flux through a closed surface is proportional to the total charge enclosed by that surface.
-
Uniformly Charged Shell: An idealized model where charge is evenly distributed over the surface of a spherical shell.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The behavior of electric field around a uniformly charged thin spherical shell can be illustrated by using a Gaussian surface to prove the field behaves as if all charge were concentrated at the center.
-
To derive the result that inside a uniformly charged shell the electric field is zero, one can use a Gaussian surface that encloses no charge.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Outside the shell, charges swell, electric fields do ring the bell. Inside the dome, calm at home, no charge to roam, you feel alone.
π Fascinating Stories
-
Imagine a party inside a dome, no noise or chaos β just calm and alone; outside, the crowd gathers near, but inside, no worries to fear, the electric field is clear.
π§ Other Memory Gems
-
Spherical Shell Electric Behavior: 'Outside is charged, inside is calm β E zero inside, think of it as a balm.'
π― Super Acronyms
ECS
- Electric field is Concentrated outside
- Shielded inside.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Spherical Shell
Definition:
A hollow sphere that has uniform charge distributed over its surface.
-
Term: Gauss's Law
Definition:
A law stating that the electric flux through a closed surface is proportional to the enclosed charge.
-
Term: Electric Field (E)
Definition:
A field around charged particles that exerts a force on other charges within the field.
-
Term: Radius (R)
Definition:
The distance from the center of the sphere to any point on its surface.
-
Term: Charge (q)
Definition:
The physical property of matter that causes it to experience a force when placed in an electromagnetic field.