Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Gauss's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore Gauss's Law, which defines the relationship between electric flux and charge. Can anyone tell me what electric flux is?
Isn't electric flux related to how many electric field lines pass through a surface?
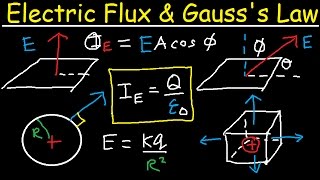
That's correct! Electric flux is proportional to the electric field and the area through which it passes. Now, Gauss's Law states that the total electric flux through a closed surface is equal to the total charge enclosed divided by the permittivity of free space. Can anyone express Gauss's Law mathematically?
It's \( \Phi_E = \frac{q_{enc}}{\varepsilon_0} \)!
Well done! This equation shows how flux relates to charge. If we know the charge inside our Gaussian surface, we can calculate the flux!
Applications of Gauss's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's apply Gauss's Law to different scenarios. For a uniformly charged sphere, what do you think happens to the electric field inside the shell?
Is it zero because of symmetry?
Exactly! Inside a charged shell, the electric field is zero. Outside, it behaves as if all the charge were concentrated at the center. Can you all recall what the electric field outside a charged sphere looks like?
It decreases like 1/r²!
Right! The electric field strength diminishes with distance. Let's look at a cylindrical charge next. What would we observe?
Example Problem on Gauss's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s apply Gauss's Law with an example. If we have a line of charge with a uniform density, how would we find the electric field using Gauss’s Law?
We can use a cylindrical Gaussian surface around the line of charge!
Yes! The electric field will be constant over the curved surface, simplifying our calculations. What is the resulting formula for the electric field from this setup?
It's \( E = \frac{\lambda}{2\pi \epsilon_0 r} \), where λ is the linear charge density!
Excellent! This highlights how powerful Gauss's Law can be in calculating the electric field for symmetrical distributions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into Gauss's Law, explaining how the electric flux through a closed surface correlates with the total charge enclosed. The implications and applications of Gauss's Law in different symmetrical charge distributions are discussed, emphasizing its utility in simplifying electric field calculations.
Detailed
Gauss's Law states that the electric flux through any closed surface is equal to the total charge enclosed by that surface divided by the permittivity of free space. Mathematically expressed as \( \Phi_E = \frac{q_{enc}}{\varepsilon_0} \), Gauss's Law is instrumental for calculating electric fields in cases of high symmetry, such as spherical, cylindrical, and planar charge distributions. This section discusses the derivation of the law using a point charge within a spherical surface and explores its application to uniformly charged lines, planes, and shells, highlighting its significance in both theoretical analysis and practical applications in electrostatics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Gauss's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As a simple application of the notion of electric flux, let us consider the total flux through a sphere of radius r, which encloses a point charge q at its centre. Divide the sphere into small area elements, as shown in Fig. 1.22.
Detailed Explanation
Gauss's Law describes the relationship between electric flux and charge. Specifically, it states how much electric field (flux) penetrates a closed surface surrounding a charge. When we have a sphere enclosing a point charge, the law helps us calculate the total flux through the surface of the sphere.
Examples & Analogies
Imagine a balloon filled with air. When you inflate the balloon, the air inside exerts pressure uniformly on the inside surface of the balloon. Similarly, electric field lines distribute themselves uniformly over the surface of the sphere, creating constant electric flux as long as the charge remains at the center.
Electric Flux Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flux through an area element DS is q\nD f= EDi =S 4p e r2 rˆiD S (1.28)\n0\nwhere we have used Coulomb’s law for the electric field due to a single charge q. The unit vector rˆ is along the radius vector from the centre to the area element. Now, since the normal to a sphere at every point is along the radius vector at that point, the area element DS and rˆ have the same direction.
Detailed Explanation
In this part, we derive the total electric flux through the sphere by integrating the electric field across the surface area. Since the electric field due to a point charge is radial, the flux through each area element of the sphere can be calculated as the product of the electric field strength and the area element.
Examples & Analogies
Think of the sun's rays entering through a circular window. The intensity of light hitting any part of the window depends on how many rays hit that area, much like the electric field hits the area element of the sphere.
Total Flux Through the Sphere
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The total flux through the sphere is obtained by adding up flux through all the different area elements: q\nf = S D =S S 4p e r2 allD S 4pe r2\n0 0\nSince each area element of the sphere is at the same distance r from the charge, S = S = S 1 2.
Detailed Explanation
By taking into account all the area elements on the surface of the sphere, we find the total flux. Because of symmetry, every area element is subject to the same electric field strength, making the calculation straightforward. We multiply the average flux over a single area element by the total surface area of the sphere to find the total flux.
Examples & Analogies
Consider measuring rainfall with a round bucket. Regardless of where the bucket is placed, as long as it is exposed to the rain, you can calculate the total volume collected by understanding how much rain falls on each area of the bucket's top surface.
Gauss’s Law Statement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
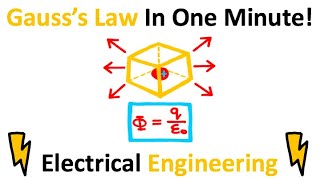
Equation (1.30) is a simple illustration of a general result of electrostatics called Gauss’s law. We state Gauss’s law without proof: Electric flux through a closed surface S = q/e (1.31) 0 q = total charge enclosed by S.
Detailed Explanation
Gauss’s law simplifies the calculation of electric fields by relating the electric flux through a closed surface to the charge enclosed by that surface. This fundamental principle holds for any shape of a closed surface, emphasizing the power of symmetries in electrostatics.
Examples & Analogies
Imagine a net that catches fish (the closed surface) in a lake where you have a specific number of fish (the charge). No matter how you position the net, the number of fish caught by it directly relates to how many fish are present in that portion of the lake.
Implications and Applications of Gauss's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The law implies that the total electric flux through a closed surface is zero if no charge is enclosed by the surface.
Detailed Explanation
When applying Gauss's law in cases where there are no charges inside the closed surface, it logically follows that the outward flux must balance itself, leading to a net flux of zero. This has practical implications for understanding electric fields in various configurations of charge.
Examples & Analogies
Think of a sealed jar that you are observing from outside. If there's nothing inside the jar, no matter how you look at it (changing angles, perspectives), you can't see anything—just as you cannot have net electric flux through a surface enclosing no charge.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Electric Flux: The product of the electric field and the area through which it passes.
-
Gauss's Law: Total electric flux through a closed surface equals the charge enclosed divided by \( \varepsilon_0 \).
-
Gaussian Surface: An imaginary closed surface used to apply Gauss's law to a charge distribution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the electric flux through a spherical surface surrounding a point charge.
-
Determining the electric field of an infinitely long uniformly charged wire using cylindrical symmetry.
Glossary of Terms
Review the Definitions for terms.
-
Term: Electric Flux
Definition:
A measure of the quantity of electric field lines passing through a surface.
-
Term: Gauss's Law
Definition:
A law stating that the electric flux through any closed surface equals the charge enclosed divided by the permittivity of free space.
-
Term: Gaussian Surface
Definition:
A closed surface used in applying Gauss's law.
-
Term: Permittivity
Definition:
A property of a material that affects how electric fields interact with it, denoted as \( \varepsilon_0 \) in free space.