Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Test Pattern Compression
Unlock Audio Lesson
Today we're going to discuss test pattern compression, which plays a crucial role in reducing test data size. Can anyone explain what we mean by test pattern compression?
Is it about making the test data smaller so we can test systems faster?
Exactly! Techniques like dictionary-based compression and run-length encoding allow us to achieve this. Remember the acronym DR—*Dictionary and Run-length*—to help you recall these methods.
How does run-length encoding work exactly?
Great question! Run-length encoding replaces sequences of repeated values with a single value and a count. This helps in significantly shrinking the size of the data we need. For example, instead of saying '0, 0, 0, 0', we can say '0 four times' which is far more compact.
Would this make the testing process faster and cheaper?
Absolutely! Let’s summarize: test pattern compression helps reduce data size, which speeds up testing and cuts costs. Remember DR next time you think about compression techniques!
Test Minimization
Unlock Audio Lesson
Now let's dive into the concept of test minimization. Why do you think minimizing test vectors is important?
Maybe to avoid testing redundancies and save time?
Exactly, Student_4! Minimization is about reducing redundancies in our test patterns using methods like greedy algorithms and genetic algorithms.
What do greedy algorithms do in this context?
Great inquiry! Greedy algorithms systematically choose the best option at each step without considering the bigger picture. This helps us find the easiest route to reduce our test vectors while achieving high fault coverage.
I've heard of genetic algorithms, but how do they apply here?
Good question! Genetic algorithms simulate the process of natural selection. They iterate through a population of test patterns over generations, gradually evolving solutions to minimize our test sets effectively. Remember, it’s like nature—only the fittest survive!
So essentially, we still get good coverage but with fewer tests?
That's right! In summary, test minimization helps maintain high fault coverage while optimizing efficiency. Excellent participation today!
Partial Scan Optimization
Unlock Audio Lesson
Let’s move on to partial scan optimization. Can anyone explain why we might want to use partial scan chains instead of full scan?
I think it’s to save on resources and speed things up.
Correct! Partial scans only put parts of a system in scan mode, which helps reduce the number of flip-flops needed for testing. This not only conserves area but also shortens testing time.
Does that affect fault coverage?
Excellent point! Even with less testing, we can still achieve high fault coverage because we target critical parts of the system. Remember the acronym PSO—*Partial Scan Optimization*—to help solidify this concept.
So we balance between doing less testing and still catching faults?
Exactly! To recap, partial scan optimization aids in efficient testing by allowing only parts of the system to be scanned. Fantastic questions and insights today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Test compression and minimization techniques are essential in modern design for testability as electronic circuits increase in complexity. These techniques enable the reduction of test data size, thus speeding up testing processes and lowering memory usage without compromising fault detection efficiency.
Detailed
Detailed Summary of Test Compression and Minimization
As electronic circuit designs grow increasingly intricate, the volume of test data required for thorough testing escalates. In response, test compression and minimization techniques have emerged as vital solutions to manage this complexity effectively. The main objectives of these techniques are to minimize the size of test patterns while ensuring that fault coverage remains high, thus leading to more efficient testing procedures.
Key Points Covered:
- Test Pattern Compression: Techniques like dictionary-based compression and run-length encoding are utilized to reduce the size of test vectors. By compressing these patterns, the amount of data involved in testing can be significantly reduced, leading to faster testing times and lower costs.
- Test Minimization: This process focuses on decreasing the number of test vectors needed to achieve satisfactory fault coverage. Methods such as greedy algorithms and genetic algorithms help in identifying and removing redundant test patterns, thus enhancing efficiency while still ensuring that faults are effectively detected.
- Partial Scan Optimization: Instead of placing entire systems in scan mode, partial scan chains allow only a subset of the system to be testable, which results in fewer flip-flops required for testing. This approach optimizes both the physical area needed for testing and reduces the runtime of the testing process while maintaining high fault coverage.
In summary, the application of test compression and minimization techniques represents a critical advancement in design for testability, addressing the challenges posed by the ever-increasing complexity of modern electronic systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Test Pattern Compression
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Techniques like dictionary-based compression and run-length encoding are used to reduce the size of test vectors. By compressing the test patterns, more compact and efficient data can be used to test large systems, which leads to reduced testing time and costs.
Detailed Explanation
Test pattern compression involves using specific methods to shrink the size of the data patterns that are used to test electronic circuits. Two popular techniques for this are dictionary-based compression and run-length encoding. Dictionary-based compression creates a dictionary of common patterns and uses shorter codes to refer to those patterns, which saves space. Run-length encoding simplifies long sequences of the same value by encoding them as a single value and a count (e.g., instead of writing '0000' four times, it can be represented as '4,0'). This reduction in data size allows more efficient testing of larger systems by speeding up the testing process and lowering the memory resources required.
Examples & Analogies
Think of a library where books represent test patterns. If each book is very large because it has extensive explanations (like uncompressed test patterns), it becomes cumbersome to manage. Now imagine if we could summarize each large book into a quick reference guide (like dictionary-based compression), which allows us to access multiple books more efficiently without needing to store all the pages. Consequently, it makes the library much more organized and easier to use—similarly, test pattern compression helps in managing data efficiently.
Test Minimization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Minimizing the number of test vectors required to achieve high fault coverage is a key focus of DFT. Greedy algorithms and genetic algorithms can be used to identify redundant test patterns and eliminate them, improving efficiency while maintaining high fault detection.
Detailed Explanation
Test minimization aims to reduce the number of test vectors—essentially, the data used to test the system—while still ensuring that all potential faults can be detected. This is critical because having too many test patterns can lead to longer testing times and more resource consumption. Techniques like greedy algorithms evaluate test patterns and gradually choose the 'best' options, discarding those that do not offer much additional value. Genetic algorithms simulate evolution by combining and mutating existing test patterns to produce a set of more efficient test vectors, eventually pruning those that are redundant but don’t contribute additional value to fault detection.
Examples & Analogies
Imagine a chef preparing a large meal with a list of ingredients. If the chef uses every ingredient in separate dishes, it can take a long time to prepare and serve. By analyzing the menu, the chef might find that some ingredients can be grouped together in fewer dishes without losing flavor (like combining redundant test patterns). This saves time, makes meal preparation faster, and reduces kitchen chaos—akin to test minimization streamlining the testing process.
Partial Scan Optimization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In some designs, partial scan chains can be employed, where only a portion of the system is placed in scan mode, reducing the number of flip-flops needed for testability. This optimizes both area and testing time, while still providing high fault coverage.
Detailed Explanation
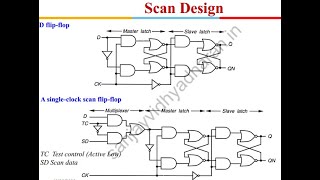
Partial scan optimization is a strategy that lets engineers focus on the most crucial parts of a system for testing rather than treating the entire system uniformly. By activating scan chains in only certain areas, designers can significantly reduce the number of flip-flops required, leading to less complexity and lowered testing times. A flip-flop is a basic memory unit used in circuits. By only scanning parts of a system where faults are more likely to occur or where fault detection is critical, this approach maintains a high level of fault coverage while cutting down on unnecessary resource usage.
Examples & Analogies
Consider a school going through an inspection where not every classroom needs to be evaluated; only the ones where students have been struggling in subjects. By focusing on the problematic classrooms, the inspection becomes more efficient and serves its purpose without overwhelming resources. This is similar to partial scan optimization, where targeting crucial parts of a system instead of scanning everything can enhance efficiency and effectiveness.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Test Pattern Compression: Techniques that reduce the size of test patterns to improve testing efficiency.
-
Test Minimization: Algorithms and strategies that aim to decrease the number of test vectors while maintaining fault detection.
-
Partial Scan Optimization: Method of implementing scan chains only in parts of the system to enhance testing performance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a scenario where a circuit has a repeated testing pattern of 0's, using run-length encoding could transform '0, 0, 0, 0' into '0 four times', decreasing data size significantly.
-
Utilizing greedy algorithms can help in determining the most effective test vectors by iteratively removing redundant patterns while ensuring fault coverage is not sacrificed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Compress your tests, avoid the mess, cut the size, and test with finesse.
📖 Fascinating Stories
-
Imagine a builder who wants to check the strength of a bridge. Instead of testing every beam, they focus on key supports to save time while ensuring stability.
🧠 Other Memory Gems
-
C-MO: Compression and Minimization Objective.
🎯 Super Acronyms
P-S-O
- Partial Scan Optimization helps us save time and costs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Test Compression
Definition:
Techniques used to reduce the size of test patterns, leading to faster testing and lower memory usage.
-
Term: Test Minimization
Definition:
Strategies aimed at minimizing the number of test vectors required to maintain high fault coverage.
-
Term: Partial Scan Optimization
Definition:
A method where only a portion of the design is placed in scan mode to reduce resource usage while maintaining fault detection effectiveness.
-
Term: DictionaryBased Compression
Definition:
A compression method that replaces patterns of test data with shorter representations using a predefined dictionary of patterns.
-
Term: RunLength Encoding
Definition:
A technique that replaces sequences of identical values with a single value and a count, thus compressing the data.