Fast Fourier Transform: Derivation of the Radix-2 FFT
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fast Fourier Transform
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore the Fast Fourier Transform, or FFT. Who knows why it's important in digital signal processing?

Isn't it faster than the regular Fourier Transform?

Exactly! The regular DFT requires O(N²) operations. The FFT reduces that to O(N log N), making it ideal for large datasets. Remember the phrase: 'FFT is Fast!' to keep this in mind!

What does O(N log N) mean in terms of performance?

Great question! It means that as our dataset grows, the time taken increases much slower compared to O(N²). So, it’s exponentially better for large N!
Breaking Down the DFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss how we can break the DFT into parts. Can anyone explain how the DFT operates?

It combines time-domain signals into their frequency components, right?

Exactly! We can split our time-domain signal into even and odd parts for computation efficiency. Who remembers what we call those?

Even-indexed and odd-indexed terms?

Perfect! This is a crucial step as it leads us to establish recursive relations in deriving the Radix-2 FFT.
Derivation of the Radix-2 FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we’ve broken down the DFT, let’s look at the derivation. What happens when we apply our even and odd sequences?

We arrive at a couple of recursive equations, right?

"Exactly! We get:
Applications of the FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What real-world applications can you think of where FFT is used?

In audio processing, like equalization or noise reduction?

Exactly! FFT is critical for tasks in audio, image processing, and even radar systems! Just remember: 'FFT for Frequencies in Time.'

So, it’s not just limited to sound, but also for images?

Absolutely! Image compression techniques like JPEG also utilize FFT. It’s a versatile tool across many digital domains.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section details the derivation of the Radix-2 FFT algorithm, illustrating its efficient computation of the Discrete Fourier Transform (DFT) using a divide-and-conquer approach. It introduces the concept of breaking the DFT into even and odd parts to optimize calculations.
Detailed
Detailed Summary of Radix-2 FFT Derivation
The Radix-2 FFT (Fast Fourier Transform) is a critical algorithm in digital signal processing, significantly enhancing the efficiency of calculating the Discrete Fourier Transform (DFT). This section outlines the derivation of the Radix-2 FFT, which operates recursively and is particularly efficient when the length of the signal is a power of two (N = 2^m).
The DFT of a sequence X[k] is computed using the complex exponential formula, which requires O(N²) operations. To address this inefficiency, the Radix-2 FFT algorithm adopts a divide-and-conquer method by splitting the DFT into two smaller DFTs—one containing even-indexed and the other odd-indexed terms. This separation leads to a recursive relation:
- X[k] = Xeven[k] + e^(-j2πk/N)
- X[k + N/2] = Xeven[k] - e^(-j2πk/N)
This process continues until the computation reduces to a two-point DFT, which requires constant time. The total computational effort is then reduced to O(N log N) thanks to the nature of recursion, where at each level of the recursion, the workload is halved. The efficient nature of the Radix-2 FFT algorithm makes it essential for various applications, including signal analysis and audio processing, enabling real-time data analysis.
Youtube Videos
![Decimation In Time - Fast Fourier Transform [Lec 2]](https://img.youtube.com/vi/XeJXx-Te1Eo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to FFT and DFT
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Fast Fourier Transform (FFT) is one of the most widely used algorithms in digital signal processing for efficiently computing the Discrete Fourier Transform (DFT). The standard DFT, although conceptually simple, requires O(N²) operations, which becomes computationally expensive for large N. The Radix-2 FFT algorithm reduces the complexity of the DFT computation to O(N log N), making it highly efficient for practical applications. In this chapter, we will derive the Radix-2 FFT algorithm, which is one of the most commonly used FFT algorithms. We will go step-by-step through the process of deriving the Radix-2 FFT and explain how it optimizes the calculation of the DFT.
Detailed Explanation
The Fast Fourier Transform (FFT) is an algorithm used to calculate the Discrete Fourier Transform (DFT) efficiently. The DFT transforms a sequence of numbers (or a signal) from the time domain to the frequency domain, allowing us to analyze its frequency content. While the DFT can be calculated directly, it requires O(N²) computational operations, which means that if the sequence (or data points) is very large, this method becomes impractical due to the time it would take. The Radix-2 FFT is a specific type of FFT that optimizes this process and reduces the number of operations needed to O(N log N). This makes a significant difference when you're working with large datasets, enabling faster computation and enabling applications in real time.
Examples & Analogies
Imagine you are trying to find the unique flavors in a very large batch of mixed ice cream. If you taste each bite individually, it would take a lot of time (akin to O(N²)). However, if you decide to split the whole batch into manageable flavors, taste each one separately, and then put those results together (this is like what Radix-2 FFT does), you'll identify the flavors much quicker (O(N log N)).
Recap on Discrete Fourier Transform (DFT)
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Discrete Fourier Transform (DFT) of a sequence x[n] of length N is defined as: X[k] = ∑ (n=0 to N−1) x[n] e^(-j 2π k n/N) for k = 0,1,…,N−1. Where:
● X[k] is the DFT of x[n].
● x[n] is the time-domain signal of length N.
● e^(-j 2π k n/N) is the complex exponential factor (the "twiddle factor").
● k is the frequency index. This direct computation of the DFT requires O(N²) operations, which becomes inefficient for large N.
Detailed Explanation
The DFT is a mathematical formula that converts a discrete series of data points (the time-domain signal) into its frequency components. Each frequency component corresponds to a specific 'k' value, indicating how much of a certain frequency is present in the original data. The equation given illustrates how each frequency component (X[k]) is calculated through the summation of the products of the input signal values and their respective complex exponential factors. However, calculating this directly for large N can quickly become computationally intensive, thus necessitating the use of algorithms like the FFT to simplify this process.
Examples & Analogies
Think of the DFT as taking apart a complex piece of machinery to see what each part does. If you have to open every single piece (like calculating each term for large N), it can take forever. The Radix-2 FFT is like having a detailed manual that tells you how to just remove certain sections to quickly analyze how the machine operates without totally disassembling it.
Overview of Radix-2 FFT
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Radix-2 FFT is a divide-and-conquer algorithm that recursively breaks down the DFT into smaller DFTs. The Radix-2 FFT works efficiently when the length of the signal N is a power of 2, i.e., N = 2^m. The main idea behind the Radix-2 FFT is to split the DFT into two smaller DFTs of half the size, compute them recursively, and combine the results. This "divide-and-conquer" approach reduces the number of operations from O(N²) to O(N log N), making it much more efficient for large datasets.
Detailed Explanation
The Radix-2 FFT works by dividing the original DFT problem into smaller pieces, which are easier to manage and compute. If N is a power of 2, the algorithm takes advantage of this by dividing the sequence into two halves: one for even indices and another for odd indices. It computes the FFT for these smaller sequences separately and then merges these results back together, effectively reconstructing the larger DFT with fewer calculations. This approach significantly reduces the number of operations needed and showcases the power of breaking down complex problems into simpler parts.
Examples & Analogies
Imagine trying to analyze a gigantic library of books. Instead of looking at each book one by one (O(N²)), you can divide the library by genres (like fiction and non-fiction) and analyze them separately. Then, you just compare the findings of each genre to get an overall understanding of the library (O(N log N)). This way, you handle the same amount of information in a fraction of the time.
Core Algorithm Steps: Breaking DFT
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
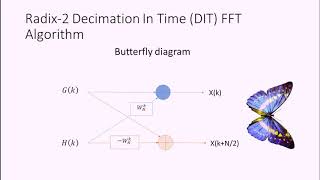
The Cooley-Tukey Radix-2 FFT algorithm is based on decomposing the DFT into two smaller DFTs by exploiting the symmetry in the complex exponentials. The first step is to split the sum into even and odd parts, allowing us to rewrite the DFT formula as:
X[k] = Xeven[k] + e^(-j 2π k/N) * Xodd[k],
X[k + N/2] = Xeven[k] - e^(-j 2π k/N) * Xodd[k]. This is the core of the Radix-2 FFT: it splits the DFT of size N into two DFTs of size N/2.
Detailed Explanation
In applying the Cooley-Tukey algorithm, first, we separate the DFT into two distinct parts: one that contains the even-indexed terms x[even] and one for the odd-indexed terms x[odd]. This results in two smaller DFTs, which can be calculated with less computational effort. The nature of the complex exponentials allows us to factor out common terms, simplifying our calculations. By defining these smaller DFTs (Xeven and Xodd), we create an efficient recursive relationship that forms the backbone of the FFT algorithm.
Examples & Analogies
Envision a bakery that decides to make a large batch of cookies (the DFT). Instead of doing everything at once (O(N²)), they separate the dough into two trays – one for chocolate chip and one for oatmeal (even and odd). They bake each tray separately (smaller DFTs) and then combine them afterward (merge results). This way, they handle the same volume of cookies more efficiently!
Key Concepts
-
Efficient Computation: Radix-2 FFT reduces the DFT complexity from O(N²) to O(N log N).
-
Recursive Splitting: The algorithm works by splitting the DFT into two smaller parts based on even and odd indexed terms.
-
Final Result Combination: Results from smaller DFTs are combined to produce the final output.
Examples & Applications
The computation of an FFT for a signal of length 8 takes significantly fewer operations than computing the DFT directly.
In audio applications, applying FFT allows for real-time audio analysis and effects processing.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For big signals, don't despair, use FFT, it makes life fair!
Stories
Imagine a baker splitting a cake into different layers to get the best layer for frosting. Similarly, FFT breaks down the data into manageable pieces for efficient processing.
Memory Tools
E.O. for Even and Odd - remember to split your data!
Acronyms
FFT = Fast Frequencies Together!
Flash Cards
Glossary
- Fast Fourier Transform (FFT)
An efficient algorithm to compute the Discrete Fourier Transform (DFT) with reduced complexity.
- Discrete Fourier Transform (DFT)
A mathematical technique for transforming a sequence of complex numbers into its frequency domain representation.
- DivideandConquer
A computational paradigm that breaks down a problem into smaller subproblems, solving each one individually.
- Complex Exponential
Functions of the form e^{-j2πkn/N}, significant in representing oscillations and waves in Fourier analysis.
Reference links
Supplementary resources to enhance your learning experience.
