Step 1: Breaking the DFT into Even and Odd Parts
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to DFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will delve into the Discrete Fourier Transform, or DFT, and see how we can make it more efficient. Can someone explain what the DFT does?

The DFT transforms a sequence of time-domain samples into their frequency-domain representation!

Exactly! It converts our time domain signals into frequency components. Why do you think understanding how to compute this efficiently is important?

Because for large datasets, the computation can become too slow!

Yes, the DFT’s complexity is O(N²), which isn’t practical for large N.

Correct! That’s why we will break it down further into even and odd parts to improve the efficiency. We call this the Radix-2 FFT.
Even and Odd Indexed Parts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s break down the DFT computation. Can anyone describe how we can split the terms in the DFT?

We can separate the sequence into even and odd indexed terms!

Absolutely! So, what would the even indexed terms look like for a sequence of length N?

It will include x[0], x[2], x[4], and so on, right?

Correct! And how about the odd indexed terms?

They would be x[1], x[3], x[5], etc.

Great! We can define those as x_even[n] and x_odd[n] for our recursive relations.
Transforming the DFT Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at how the DFT representation changes when we apply this partition. Who can write the new DFT equation?

The DFT X[k] can be written as the sum of two parts: the even and the odd indexed terms!

Correct! It simplifies to X[k] = X_even[k] + e^(-j2πk/N) * X_odd[k]. Why is this separation key?

Because it allows us to compute smaller DFTs recursively, which saves time!

Exactly! This recursive approach is what makes the Radix-2 FFT so powerful. Keep in mind that we also have a second formula for X[k + N/2].
Recap and Importance of the Step
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To wrap up today’s lesson, what did we learn from breaking the DFT into even and odd parts?

We learned how to separate the DFT computation into two smaller parts, which can be computed recursively.

And this reduces the computational complexity from O(N²) to O(N log N)!

Perfect! Understanding this step is vital for grasping how FFT works. In our next lesson, we will explore the recursive computation further.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explains how the DFT can be efficiently computed by splitting the sequence into even and odd indexed terms, facilitating the recursive computation necessary for the Radix-2 FFT algorithm, thus substantially reducing computational complexity.
Detailed
In this section, we explore the first step in deriving the Radix-2 Fast Fourier Transform (FFT) algorithm by dissecting the Discrete Fourier Transform (DFT) into even and odd indexed parts. For a sequence of length N (where N is a power of 2), the algorithm divides the DFT calculation into two separate summations: one for even indexed terms and another for odd indexed terms. This approach allows denoting the even terms as x_even[n] and the odd terms as x_odd[n], leading to a simplified recursive relation for each part's DFT, X_even[k] and X_odd[k]. This division is crucial, as it reduces the complexity of the computation, paving the way for the efficient processing capabilities of the Radix-2 FFT.
Youtube Videos
![Decimation In Time - Fast Fourier Transform [Lec 2]](https://img.youtube.com/vi/XeJXx-Te1Eo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to DFT Splitting
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
First, observe that the DFT sum involves complex exponentials e−j2πknN. We can split this sum into two parts: one for the even-indexed terms and one for the odd-indexed terms.
Detailed Explanation
The Discrete Fourier Transform (DFT) computes the frequency components of a signal by summing over complex exponentials. In this approach, we notice that we can simplify the calculation by separating the terms based on their indices. Specifically, we can identify terms that fall on even indices and terms that fall on odd indices. This separation will help us handle the computation more efficiently.
Examples & Analogies
Imagine you’re organizing a party and you have two groups of people: those who RSVP'd early and those who RSVP'd late. Instead of trying to handle all invitees at once, you first organize the early RSVP group, then the late group. This makes the planning much simpler and organized.
Defining Even and Odd Sub-sequences
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For N=2^m, split the sequence x[n] into two subsequences: ● Even-indexed terms: x[0], x[2], x[4],… ● Odd-indexed terms: x[1], x[3], x[5],… Let xeven[n]=x[2n] and xodd[n]=x[2n+1].
Detailed Explanation
When we have a sequence of data points of length N that is a power of two, we can create two new sequences: one containing the data from the even indices (like 0, 2, 4) and another with data from the odd indices (like 1, 3, 5). We define these new sequences as xeven[n] for even and xodd[n] for odd, using indexing to conveniently extract each subsequence. This allows us to modularize our computations by focusing on smaller pieces.
Examples & Analogies
Think of a deck of playing cards shuffled together. If you want to sort them faster, you might first split the deck into even and odd numbered cards. Sorting these smaller piles separately is often easier than dealing with the entire deck at once.
Rewriting the DFT
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Rewrite the DFT as: X[k]=∑n=0N/2−1x[2n]e−j2πkN(2n)+∑n=0N/2−1x[2n+1]e−j2πkN(2n+1)
Detailed Explanation
With the established definitions of our even and odd sequences, we can rewrite the DFT formula to specify that we'll evaluate two sums. The first sum corresponds to the even-indexed terms, while the second sum is for the odd-indexed terms. Each term in the DFT is computed separately based on whether the index is even or odd, and this reduces the overall complexity of the computation.
Examples & Analogies
Consider analyzing two separate music tracks: one contains all the upbeat songs (even indices) and the other has the slower tunes (odd indices). If you treat each track individually first, you can clearly see the trends and beats in each before trying to merge them back into your overall playlist.
Simplifying the DFT Expression
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This simplifies to: X[k]=∑n=0N/2−1xeven[n]e−j2πkN(2n)+e−j2πkN∑n=0N/2−1xodd[n]e−j2πkN(2n)
Detailed Explanation
The rewrite allows us to further simplify our DFT representation. By using our defined even and odd sequences, we express the DFT in terms of these subsequences combined with the complex exponential factors. This sets the stage for us to work with smaller DFT computations rather than the whole sequence.
Examples & Analogies
If you have a task of painting a large mural, it could be daunting to think about the entire wall at once. Instead, if you focus on painting small sections (like one color at a time), you simplify and strategize your work, making it feel less overwhelming.
Introducing Recursive Relations
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
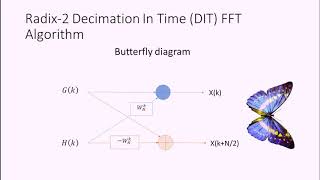
By defining Xeven[k] and Xodd[k] as the DFTs of the even-indexed and odd-indexed subsequences, respectively, we get the following recursive relation: X[k]=Xeven[k]+e−j2πkNXodd[k] and X[k+N/2]=Xeven[k]−e−j2πkNXodd[k].
Detailed Explanation
Now that we have defined our even and odd subsequences, we can express the original DFT in terms of the DFTs of these two subsequences (Xeven and Xodd). This creates recursive relations which form the foundation of the Radix-2 FFT. Using these relations, we can compute the DFT for a larger signal by combining the results of smaller DFTs, leading to a significant reduction in computational complexity.
Examples & Analogies
When working on a large project, instead of tackling everything at once, you break it down into smaller tasks. By completing each task one by one, you can combine your results into a final product. This is similar to how we can combine the results of the DFT from the even and odd parts to construct the full DFT.
Key Concepts
-
Partitioning DFT: The DFT can be broken into components based on parity (even and odd indices).
-
Recursive relation: The DFT can be recursively related through its even and odd indexed parts.
-
Computational Efficiency: This partition reduces overall computation time and improves efficiency in processing.
Examples & Applications
For an input sequence of length N=8, the even indexed sequence would be (x[0], x[2], x[4], x[6]) while the odd indexed would be (x[1], x[3], x[5], x[7]).
If x[n] = {1, 2, 3, 4, 5, 6, 7, 8}, then x_even[n] = {1, 3, 5, 7} and x_odd[n] = {2, 4, 6, 8}.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To FFT we partition, even and odd with ambition. Splitting helps compute, efficiently in pursuit!
Stories
Imagine a baker with a large cake, cutting it into halves to bake quicker pieces, just like splitting the DFT for speed!
Memory Tools
E-O-M is for Even-Odd-Multiply: E for Even, O for Odd, M means multiply their results.
Acronyms
SPEED
Splitting Proves Efficiently Easier DFT!
Flash Cards
Glossary
- DFT (Discrete Fourier Transform)
A mathematical technique used to convert a sequence of time-domain signals into their frequency-domain representation.
- Radix2 FFT
An efficient algorithm for computing the DFT that reduces time complexity from O(N²) to O(N log N) by recursively dividing the problem into smaller components.
- Evenindexed terms
Terms of a sequence that are placed at positions which are even numbers (e.g., x[0], x[2], x[4],...).
- Oddindexed terms
Terms of a sequence that are placed at positions which are odd numbers (e.g., x[1], x[3], x[5],...).
Reference links
Supplementary resources to enhance your learning experience.
