Radix-2 FFT: Overview
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Radix-2 FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll dive into the Radix-2 FFT algorithm, which helps us compute the Discrete Fourier Transform more efficiently. Can anyone tell me why we need a more efficient method?

Is it because the direct method takes a lot of time for larger datasets?

Exactly! The direct computation takes O(N^2) operations. Now, what if I told you that the Radix-2 FFT reduces that to O(N log N)?

Wow, that’s a huge difference! How does it do that?

Great question! The key is a divide-and-conquer strategy. It breaks the problem down into smaller, manageable DFTs.

What does that splitting look like?

We'll get there! Each DFT of even and odd indexed samples can be computed recursively.

To summarize, Radix-2 FFT enhances efficiency significantly, making it more practical for large datasets.
Mechanics of Radix-2 FFT
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

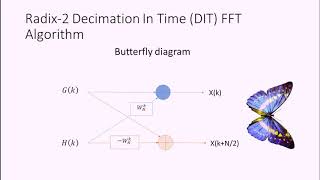
Let’s discuss how Radix-2 FFT actually splits the DFT. What do we do with the DFT sum of complex exponentials?

We can separate the sum into even and odd indexed terms, right?

Exactly! By defining the even and odd indexed terms as separate sequences, we simplify the problem.

What’s the next step once we split them?

We compute their DFTs and combine them using the derived equations. Can anyone summarize this step?

We combine X_even[k] and X_odd[k] using the equations we learned!

Great recap! By recursively applying this method, we make the computation highly efficient.
The Recursion and Base Cases
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, how does the recursion work in Radix-2 FFT? What do we hit when we split too far?

We reach the base case of size 2!

Right! And how straightforward is that computation?

It's just a couple of additions and subtractions!

Correct! Once the base cases are computed, we combine results. Let’s summarize what we’ve learned.

In essence, the Radix-2 FFT involves splitting, recursive computations, and simplification to manage large datasets effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the Radix-2 FFT algorithm, which efficiently computes the DFT by recursively dividing it into smaller DFTs. This approach significantly lowers computational complexity, making it suitable for large datasets. The process involves splitting the input signal based on even and odd indices and combining the results to achieve the final DFT.
Detailed
Radix-2 FFT: Overview
The Radix-2 Fast Fourier Transform (FFT) is a highly efficient algorithm for calculating the Discrete Fourier Transform (DFT) of a sequence. By utilizing a divide-and-conquer strategy, the Radix-2 FFT breaks the DFT computation into two smaller DFTs, one for even-indexed samples and another for odd-indexed samples. This algorithm is particularly effective when the number of samples, denoted as N, is a power of two (N=2^m).
The significance of this method lies in its ability to reduce the number of operations from O(N^2), inherent in direct DFT calculations, to O(N log N). The process is recursive, continuing to split the DFTs until reaching base cases of size 2, which can be computed directly. Ultimately, by combining the results from smaller DFTs, the Radix-2 FFT provides a rapid means of performing frequency analysis, making it invaluable for applications in digital signal processing, audio analysis, and many other fields.
Youtube Videos
![Decimation In Time - Fast Fourier Transform [Lec 2]](https://img.youtube.com/vi/XeJXx-Te1Eo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Radix-2 FFT
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The Radix-2 FFT is a divide-and-conquer algorithm that recursively breaks down the DFT into smaller DFTs. The Radix-2 FFT works efficiently when the length of the signal N is a power of 2, i.e., N=2^m.
Detailed Explanation
The Radix-2 FFT takes a large problem (calculating the DFT) and breaks it into smaller, more manageable problems. It does this by splitting the DFT into two smaller DFTs of half the size. This is especially useful when the length of the input signal is a power of 2, such as 2, 4, 8, 16, etc. This approach allows for a more organized and efficient calculation.
Examples & Analogies
Think of the Radix-2 FFT like a large organization preparing for an event. If the organization can break down responsibilities into smaller teams, each focusing on a specific task, the entire project can be completed more quickly and efficiently, just as smaller DFTs can be computed faster than one large DFT.
Efficiency of Radix-2 FFT
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The main idea behind the Radix-2 FFT is to split the DFT into two smaller DFTs of half the size, compute them recursively, and combine the results. This 'divide-and-conquer' approach reduces the number of operations from O(N^2) to O(N log N), making it much more efficient for large datasets.
Detailed Explanation
By splitting the DFT into two smaller components repeatedly, the Radix-2 FFT minimizes computational efforts significantly. Instead of processing all data at once, it handles smaller chunks. This reduction from O(N^2) operations to O(N log N) means that large datasets can be analyzed with much faster computation speeds, which is crucial in real-time applications.
Examples & Analogies
Consider a library with thousands of books. If a librarian tries to find a specific book by looking through all the shelves at once, it will take a long time. However, if the librarian first checks each section and narrows it down to a few shelves, finding the book can happen much faster. This is similar to how the Radix-2 FFT makes it quicker to find the solution to the DFT.
Key Concepts
-
Radix-2 FFT: An algorithm optimizing DFT computation through recursion.
-
Divide-and-Conquer: A strategy that divides problems into smaller manageable ones.
-
Complex Exponential: Fundamental to DFT formulation, represented by e^{-j2πk n/N}.
Examples & Applications
If we apply Radix-2 FFT on a signal with 8 points, it splits the computation into two 4-point DFTs, which further split into two 2-point DFTs.
The complexity reduction from O(N^2) to O(N log N) enables real-time processing of audio signals with thousands of data points.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the numbers are ripe, split them in two, FFT will help, and save you some stew.
Stories
Imagine a library where each book is a signal. By splitting the books into two sections, the librarian can quickly find the right one using FFT.
Memory Tools
Remember DFT: Divide, Find, Combine, Transform!
Acronyms
FFT
Fast Finding Transform
where we find speed in the waves!
Flash Cards
Glossary
- Fast Fourier Transform (FFT)
An efficient algorithm to compute the Discrete Fourier Transform (DFT) of a sequence.
- Discrete Fourier Transform (DFT)
A mathematical transformation employed to analyze the frequencies contained in a sampled signal.
- Radix2 FFT
A specific FFT algorithm designed to operate efficiently on sequences whose length is a power of 2.
- DivideandConquer
An algorithm design paradigm that breaks a problem into smaller sub-problems, solves them independently, and combines their solutions.
- Complex Exponential
A mathematical function used in the formulation of the DFT, expressed in the form e^{-j2πk n/N}.
Reference links
Supplementary resources to enhance your learning experience.
