Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to 2-DOF systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we will discuss the concept of a Two Degree of Freedom system. This dynamic system has two independent coordinates for motion. Can anyone provide an example of where such a system might be found?
How about in a two-story building?
Exactly! A two-story shear building is a perfect example. It illustrates how each story can move independently.
What components do we usually see in these systems?
Great question! Typically, they consist of two masses connected by springs or dampers. This connection allows them to share vibrational forces.
Examples of 2-DOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s delve into some examples of 2-DOF systems. We have the two-story shear building and another example is the two-mass torsional vibration system. Can anyone explain how these connect to real-world engineering?
I think in bridges, the mass at the deck and the flexibility of the pylons work as a 2-DOF system!
Exactly! These models simplify complex interactions, making it easier to analyze dynamic behaviors.
Why is understanding these systems important for earthquake design?
Great question! Understanding 2-DOF systems helps us predict how structures will react during earthquakes, potentially leading to better designs.
Dynamic Characteristics of 2-DOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the basic examples, let’s dive into their dynamic characteristics. What happens when these systems experience vibrations?
Do they have mode shapes like SDOF systems?
Exactly! 2-DOF systems exhibit multiple mode shapes and natural frequencies, making them unique.
How do engineers calculate these frequencies?
Great question! They typically set up the equations of motion using matrices to find eigenvalues. This approach helps us predict various response scenarios.
What role does damping play in these systems?
Damping reduces resonance effects and helps dissipate energy during dynamic loading. It’s crucial for ensuring structural integrity during events like earthquakes.
Importance of 2-DOF in Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, let us discuss the significance of 2-DOF systems in engineering. What functions do they hold in modern structural design?
Are they used just for new structures or also for retrofitting existing ones?
Both! Understanding 2-DOF systems is pivotal in both designing new structures and retrofitting older buildings for earthquake resilience.
So, they help in calculating risk and determining appropriate design adaptations?
Absolutely! They help engineers analyze how multi-story structures respond to seismic events and guide appropriate design adjustments.
Can we use a computer simulation to model these behaviors?
Yes! Computational tools like MATLAB are very effective for simulating and analyzing these systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the Two Degree of Freedom (2-DOF) system, a dynamic model that necessitates two independent coordinates to describe its motion. Key examples, including two-story shear buildings and torsional systems, illustrate its application. Understanding 2-DOF systems is crucial for analyzing coupled vibration modes and enhancing earthquake resilience in structural design.
Detailed
Two Degree of Freedom System
The Two Degree of Freedom (2-DOF) system is fundamental in structural dynamics, particularly when assessing complex architectural frameworks such as bridges and high-rise buildings. Unlike Single Degree of Freedom (SDOF) systems, which focus on simpler models, 2-DOF systems incorporate two independent moving components or masses, allowing for dynamic complexities like coupled vibrations.
Key Characteristics:
- Definition: A 2-DOF system necessitates two independent coordinates for a complete description of motion, typically modeled with two masses linked by springs or dampers.
- Key Examples:
- Two-story shear buildings.
- Two-mass torsional vibration systems.
- Rigid beams supported by two flexible connections.
Such systems are paramount in the study of modal analysis, resonance, and modal participation—critical factors for designing structures resilient to seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of 2-DOF System
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
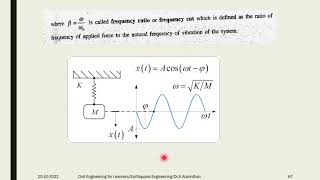
A 2-DOF system is defined as a dynamic system that requires two independent coordinates to describe its motion completely. These systems typically consist of two masses connected by springs and/or dampers, each capable of independent translational or rotational movement.
Detailed Explanation
A Two Degree of Freedom (2-DOF) system is essentially a way to describe the motion of a dynamic system that cannot be understood with a single coordinate alone. It requires two independent coordinates to fully define the system's behavior over time. Think of it like needing two keys to open a door. In this case, you have two masses, which can move or rotate independently from each other, connected by springs and dampers that help to control their motion. This allows them to respond to forces in distinct ways, making it significant for designing complex structures.
Examples & Analogies
Imagine a swing and a pendulum: if you only consider one of them, you miss out on the multipath interaction. A child on a double swing can move forward and side-to-side independently, much like how both masses in a 2-DOF system move independently, influenced by the balance of forces acting on them.
Examples of 2-DOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example Systems:
• Two-story shear building
• Two-mass torsional vibration system
• Rigid beam supported by two flexible supports
Detailed Explanation
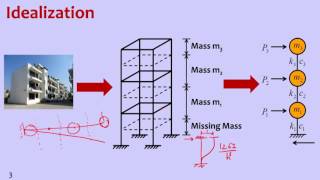
The examples given illustrate practical applications of 2-DOF systems. A two-story shear building can be modeled as a 2-DOF system where each floor represents one mass, and their interactions and movement through springs represent the structural elements that absorb energy during shifts. Similarly, a two-mass torsional vibration system reflects how different parts of structures can twist and move separately, revealing how complex interactions occur during dynamic loading, such as wind or seismic activity. Finally, the rigid beam supported by flexible supports displays how independence between supports and the beam allows for various motion responses.
Examples & Analogies
Consider skyscrapers during strong winds: the different floors may sway independently while still being tethered to the building's foundation, much like the individual masses in our examples. This interaction is critical for designing buildings that can withstand lateral forces without collapsing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
2-DOF Definition: A dynamic system that requires two independent coordinates.
-
Applications: Foundational for analyzing complex structures like buildings and bridges.
-
Importance: Essential for understanding seismic response and resonance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A two-story shear building modeled as a 2-DOF system with independent motion at each level.
-
A two-mass torsional vibration system where masses are linked and exhibit coupled vibrations during dynamic loading.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a 2-DOF duo, they dance in a row, each with a motion, where energy flows.
📖 Fascinating Stories
-
Once in a rigid building with two stories, each floor could sway independently to avoid seismic worries.
🧠 Other Memory Gems
-
M C S - Masses, Coupling, Stiffness: Remember the essentials of a 2-DOF system!
🎯 Super Acronyms
2-DOF
- Two Degrees Of Freedom - our key to structural insight!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Two Degree of Freedom (2DOF)
Definition:
A dynamic system requiring two independent coordinates to completely describe its motion.
-
Term: Modal Analysis
Definition:
A method to determine the natural frequencies and mode shapes of a system.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.
-
Term: Mode Shape
Definition:
The shape that a structure takes when vibrating at a particular natural frequency.
-
Term: Eigenvalue Problem
Definition:
A mathematical problem used to determine the natural frequencies and mode shapes of a system through matrix equations.
-
Term: Coupled Modes
Definition:
Interaction between different vibrational modes in a system.