Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Shapes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to explore the concept of mode shapes in a two degree of freedom system. Mode shapes are crucial because they describe specific patterns of motion in vibrating systems.
How do we know if two mode shapes are different? What does it mean for them to be 'normalized'?
Great question! Two mode shapes are considered different if they correspond to different frequencies of vibration. Normalization means that the mode shapes are scaled so that their energy distribution is uniform, typically making their length equal to one.
So, how do we use these shapes in our equations?
By substituting these normalized mode shapes into our equations of motion, we can simplify complex calculations. Do you remember the equations that describe the motion of our system?
Is that the Mx¨ + Kx = 0 equation?
Exactly! By transforming these equations into modal coordinates using our mode shapes, we can decouple them, significantly simplifying our analysis.
To summarize, normalized mode shapes help us understand the different modes of vibration in a system and simplify calculations through orthogonality. Any final questions?
Understanding Orthogonality
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s dive deeper into orthogonality. There are two specific conditions we need to understand: mass-orthogonality and stiffness-orthogonality.
What are those conditions again?
Mass-orthogonality states that the dot product of different normalized mode shapes with the mass matrix M equals zero when i is not equal to j. This means they do not interact in terms of mass distribution.
And what about stiffness-orthogonality?
Stiffness-orthogonality indicates that the same dot product, but with the stiffness matrix K, also equals zero under the same conditions. This implies there is no coupling in terms of stiffness.
So, this makes our equations easier to solve?
Exactly! These conditions allow us to decouple our equations, transforming a complex system into simpler independent equations, making analysis much more manageable.
Remember, orthogonality is key for effective modal analysis! Ready to move on?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The orthogonality condition of normalized mode shapes allows for the simplification of modal analysis. It illustrates how the equations of motion can be decoupled when transformed into modal coordinates, facilitating a clearer understanding of the dynamic behavior of multi-degree-of-freedom systems.
Detailed
Orthogonality of Mode Shapes
In this section, we address the important concept of the orthogonality of mode shapes within the context of two degree of freedom (2-DOF) systems. For normalized mode shapes C6i and C6j, the following orthogonality conditions hold:
-
Mass-Orthogonality:
C6iTMC6j = 0 for i ≠ j
This indicates that the inner product with the mass matrix of different mode shapes is zero, highlighting their independence in terms of mass distribution. -
Stiffness-Orthogonality:
C6iTKC6j = 0 for i ≠ j
This condition demonstrates that different mode shapes do not couple within the stiffness framework, facilitating a clear separation of vibrational modes.
These orthogonality properties significantly simplify modal analysis. By transforming the equations of motion into modal coordinates, we can decouple complex equations governing the motion of multi-degree-of-freedom systems. This decoupling is pivotal for accurately evaluating system behaviors, particularly in applications related to structural dynamics and seismic response analysis.
Youtube Videos
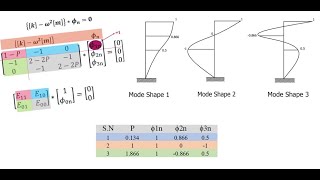
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Normalized Mode Shapes and Orthogonality Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If ϕ and ϕ are the normalized mode shapes, they satisfy the orthogonality condition:
ϕTMϕ =0 for i̸=j
ϕTKϕ =0 for i̸=j
Detailed Explanation
In this chunk, we introduce the concept of normalized mode shapes, denoted as ϕ₁ and ϕ₂. Orthogonality conditions mean that if you check the inner product of two different mode shapes, the result will be zero. This applies to both the mass matrix (M) and the stiffness matrix (K). The first equation states that when you multiply a mode shape with the mass matrix and another mode shape, the result is zero if the modes are different (i.e., i ≠ j). Similarly, the second equation tells us that the same holds for the stiffness matrix. This property is significant because it indicates that the vibration modes do not interact with one another; they are independent.
Examples & Analogies
Think of orthogonality like two people dancing in a space. If one person is spinning in a circle (representing the first mode shape) and another is just standing still (a point of zero movement, representing the second mode), their movements do not interfere with one another. This means they can move without affecting each other, much like how different mode shapes operate in a dynamic system.
Implications of Orthogonality in Modal Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Orthogonality simplifies modal analysis by decoupling the equations of motion when transformed into modal coordinates.
Detailed Explanation
The orthogonality of mode shapes profoundly impacts how we analyze the dynamic behavior of structures. When we transform the equations of motion into modal coordinates using these mode shapes, the orthogonal property allows us to decouple the equations. This means that each mode can be analyzed independently without interference from any other mode. This simplification makes it easier to predict how a structure will react to external forces, such as during an earthquake, because we can consider each mode of vibration separately.
Examples & Analogies
Imagine a symphony orchestra where each musician plays a different instrument. If all musicians play their parts independently and stay in tune (orthogonality), the final music sounds harmonious. If one musician plays out of tune or too loudly (like a coupled mode), it disrupts the performance. In structural analysis, ensuring that modes are orthogonal allows us to understand the system without complicated noise from other modes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass-Orthogonality: Mode shapes corresponding to different natural frequencies have an inner product of zero with the mass matrix.
-
Stiffness-Orthogonality: Mode shapes corresponding to different natural frequencies have an inner product of zero with the stiffness matrix.
-
Normalized Mode Shapes: Mode shapes are scaled to have a length of one, simplifying analysis.
-
Decoupled Equations: Orthogonality allows the transformation of complex equations into simpler independent equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For a 2-DOF system with normalized mode shapes, if C61 and C62 are the two shapes, then C61TMC62 = 0 demonstrating mass-orthogonality.
-
In structural dynamics, if a building's vibration modes are represented by two normalized mode shapes, the decoupling of its dynamic equations allows engineers to assess each mode independently during seismic analysis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Orthogonal vibes dance so free, mass and stiffness, zero they be.
📖 Fascinating Stories
-
Once upon a time, two dancers, Mass and Stiffness, discovered the secret to their independence. They danced in harmony without stepping on each other's toes, showing that no matter how close they were, they remained perfectly orthogonal!
🧠 Other Memory Gems
-
For mode shapes: M = Mass, K = Kinetic energy during vibration. Remember: M and K together means no interaction for non-mixed vibes.
🎯 Super Acronyms
N.O.M. - Normalized Orthogonal Modes to remember that modes are both normalized and orthogonal!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Shape
Definition:
A specific pattern of motion that a system can exhibit when vibrating at its natural frequency.
-
Term: Orthogonality
Definition:
A mathematical condition where two functions or vectors are independent of each other, meaning they do not influence each other's behavior.
-
Term: Normalized Mode Shapes
Definition:
Mode shapes that have been scaled to have a unit length to facilitate mathematical analysis.
-
Term: Mass Matrix
Definition:
A matrix that represents the distribution of mass in a system.
-
Term: Stiffness Matrix
Definition:
A matrix that represents the rigidity of a system.