Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Eigenvalue Problems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to talk about how we can determine the natural frequencies and mode shapes in a two-degree of freedom system. We start with the equation of motion: Mx'' + Kx = 0. Can anyone tell me what these terms refer to?
M is the mass matrix and K is the stiffness matrix.
Exactly! So, when we substitute our assumed solution \(x(t) = \Phi e^{i\omega t}\) into this equation, we get an eigenvalue problem. What does this mean?
It helps us find the natural frequencies and corresponding mode shapes.
Correct! The eigenvalue problem we form is \(\text{det}(K - \omega^2 M) = 0\), which we will solve for frequencies.
So, can we think of \(\omega\) as how fast the system will vibrate?
Yes, that's a great way to see it! Let's summarize: We substitute harmonic motion into our equation, leading us to determine our natural frequencies.
Mode Shapes Importance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s discuss mode shapes. What do you think mode shapes represent in our 2-DOF system?
Are they the patterns of motion that each part of the structure will move in during vibration?
Precisely! Each mode shape indicates how each mass in a system moves in relation to one another during vibration. Why might this be important for engineers?
Understanding these shapes helps in designing structures that can withstand vibrations.
Exactly! This knowledge is vital for ensuring the structural integrity during seismic events.
Are there always two mode shapes in a 2-DOF system?
Yes, that's right. For each natural frequency, there’s a corresponding mode shape. Remember, we found both through our eigenvalue problem.
Application of Natural Frequencies
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s shift to how we apply natural frequencies and mode shapes in real engineering. Why do we care about these values in structural engineering?
They help predict how a structure will react to earthquakes or other dynamic loads.
Exactly! Knowing the natural frequencies helps in assessing resonance risk. Can someone explain what resonance means?
It’s when the frequency of the load matches a natural frequency, causing potentially dangerous vibrations.
Great answer! Engineers use this information to refine their designs, ensuring that we avoid this resonance condition during seismic events.
So by understanding mode shapes, we can also consider how different parts of the structure will interact?
Yes! You’re grasping it well! Understanding both natural frequencies and mode shapes gives us a comprehensive view of structural dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how the equations of motion in a two-degree of freedom system can be converted into a standard eigenvalue problem. This process allows us to find the natural frequencies and their corresponding mode shapes, which are essential in understanding the dynamic behavior of structures during vibrations.
Detailed
Detailed Summary
In this section, we analyze the behavior of a two-degree of freedom (2-DOF) system by solving the homogeneous equation of motion represented in matrix form as \(Mx'' + Kx = 0\). By assuming harmonic motion in the form \(x(t) = \Phi e^{i\omega t}\), where \(\Phi\) represents the mode shapes and \(\omega\) the natural frequencies, we substitute this expression into the motion equation. This leads to the standard eigenvalue problem:
\(\text{det}(K - \omega^2 M) = 0\)
Solving this determinant yields two natural frequencies, denoted as \(\omega_1\) and \(\omega_2\), and the corresponding eigenvectors give the mode shapes \(\phi_1\) and \(\phi_2\). Understanding these natural frequencies and mode shapes is critical in the context of seismic engineering, as it helps in analyzing the dynamic response of structures subjected to external forces and vibrations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Harmonic Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To solve the homogeneous system:
Mx¨+Kx=0
Assume harmonic motion:
x(t)=Φeiωt
Detailed Explanation
In this chunk, we are looking at how to solve the motion of a dynamic system represented by matrices M and K. The first part reaffirms that we want to find solutions for the equation Mẍ + Kx = 0, which describes undamped vibration. The term 'harmonic motion' refers to a type of periodic movement that repeats at regular intervals. By assuming a solution of the form x(t) = Φe^(iωt), where Φ is the mode shape and ω is the frequency, we simplify the problem of finding the natural frequencies and mode shapes of the structure.
Examples & Analogies
Think of a swing at a playground. When you push the swing, it moves back and forth in a harmonic fashion. If you measure its motion over time, you can see a pattern that looks like sine waves. Just like that swing, structures vibrate in predictable patterns during events like earthquakes, which we analyze using equations in dynamic systems.
Formulation of the Standard Eigenvalue Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Substitute into the equation to obtain:
(−ω²M+K)Φ=0
This is a standard eigenvalue problem:
det(K−ω²M)=0
Detailed Explanation
After substituting the assumed solution back into the equation, we simplify it to create a form that looks like a standard mathematical problem known as an eigenvalue problem. The equation (−ω²M + K)Φ = 0 is fundamental in determining the characteristics of the system. The determinant condition det(K - ω²M) = 0 indicates that we are looking for specific frequencies (natural frequencies) and corresponding vectors (mode shapes) that balance the stiffness of the system against its mass. These eigenvalues (ω²) will help us understand how the structure will behave when subjected to dynamic loads.
Examples & Analogies
Imagine tuning a guitar. Each string has a specific frequency at which it vibrates best. When you pluck a string, it resonates at its natural frequency. The eigenvalue problem is like figuring out the optimal tension and length needed to achieve the right pitch so the string vibrates harmoniously, just as we want our structures to vibrate safely under loads.
Natural Frequencies and Mode Shapes Extraction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solving this gives two natural frequencies: ω₁,ω₂. The corresponding eigenvectors give the mode shapes ϕ₁,ϕ₂.
Detailed Explanation
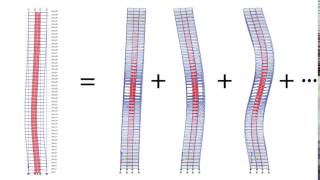
When we solve the eigenvalue problem, we find two distinct natural frequencies, denoted as ω₁ and ω₂. These frequencies are critical because they tell us how the system will respond to dynamic loads. Along with this, we also derive mode shapes ϕ₁ and ϕ₂, which indicate the manner in which the structure will deform at those frequencies. Each mode shape provides a visual or mathematical representation of displacement patterns that occur at the natural frequencies.
Examples & Analogies
Think of a trampoline. When someone jumps on it, the trampoline can vibrate at certain frequencies. These frequencies and the way the surface moves (the mode shapes) depend on how heavy the person is and how they jump. If you added more people, each would create its own pattern of movement, similar to how different modes relate to different frequencies in a 2-DOF system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Natural Frequencies: Frequencies at which a system vibrates naturally.
-
Mode Shapes: Patterns of motion corresponding to each natural frequency.
-
Eigenvalue Problems: Mathematical formulations used to derive natural frequencies and mode shapes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A two-story shear building can be modeled as a 2-DOF system to analyze its response during seismic events.
-
A rigid beam supported at two flexible points can illustrate natural frequencies and corresponding mode shapes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a two DOF sway, frequencies play, modes sway in patterns, guiding the way.
📖 Fascinating Stories
-
Imagine a dancer on two strings, swaying back and forth. As she finds her rhythm, she moves in a pattern, that’s her mode shape; the beat of her steps represents the natural frequency.
🧠 Other Memory Gems
-
Frequencies and Flexibilities - F2 = (Natural Frequencies, Mode Shapes).
🎯 Super Acronyms
NOM - Natural (Frequency), Oscillations (Mode), Matrix (Eigenvalue problem).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.
-
Term: Mode Shape
Definition:
The specific pattern of motion in which each part of the system moves relative to each other during oscillation.
-
Term: Eigenvalue Problem
Definition:
A mathematical problem for determining the eigenvalues (natural frequencies) and eigenvectors (mode shapes) of a system.