Forced Vibration and Modal Analysis
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Forced Vibration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore what happens to our two degree of freedom system when an external force is applied. Can anyone remind us what we mean by a 'two degree of freedom system'?

It's a dynamic system that requires two independent coordinates to describe its motion!

Exactly! Now, when we apply an external force F(t), the equation governing our system becomes Mx¨ + Kx = F(t). This represents the dynamics of the system. What do you think 'M' and 'K' stand for?

M is the mass matrix and K is the stiffness matrix, right?

Correct! And understanding these matrices helps in analyzing how forces affect the motion of the structure.
Modal Transformation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about modal transformation. When we express our system's motion with modal coordinates, we use x(t) = Φq(t). What does this achieve?

It simplifies the equations to make them easier to analyze!

Right you are! By transforming the equations, we get q¨ + Ω²q = Φ^T F(t). This allows us to work with uncoupled equations. How can this be useful in practical scenarios?

It allows each mode to be analyzed independently, which can save a lot of time in calculations!
Significance of Modal Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We've covered that modal analysis allows us to assess the responses of each mode independently. Can anyone give me an example where this could be critical?

During an earthquake, we need to understand how different modes of the structure would respond to ground motion!

Exactly! Understanding this helps engineers design structures that can withstand seismic forces effectively.

So modal participation factors are also important?

Yes! They allow us to determine how much energy from a seismic event is distributed to each mode, enhancing our understanding of structural dynamics.
Recap & Key Takeaways
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

So let’s recap what we've learned about forced vibration and modal analysis. What are the primary equations we discussed?

Mx¨ + Kx = F(t) and q¨ + Ω²q = Φ^T F(t)!

Great recall! And how do we benefit from using modal transformation?

It simplifies the analysis by uncoupling the modal equations!

Correct! Understanding these concepts equips us to handle real-world applications effectively. Excellent work today!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the dynamics of a forced 2-DOF system are examined, highlighting how modal transformation can simplify the equations of motion. The section emphasizes the significance of modal coordinates in analyzing uncoupled modal equations, allowing for individual component analysis under external forces.
Detailed
Forced Vibration and Modal Analysis
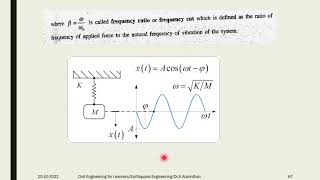
In structural dynamics, understanding how a two degree of freedom (2-DOF) system responds to external forces is crucial for both practical engineering and theoretical study. When an external force F(t) is applied to the system, we represent the motion through the equation:
$$ M\ddot{x} + Kx = F(t) $$
Here, the matrix formulation facilitates the transformation of the equation into modal coordinates using:
$$ x(t) = \Phi q(t) $$
where \( \Phi \) is the mode shape matrix and \( q(t) \) is the vector of modal coordinates. The equations are subsequently transformed to a simpler format:
$$ \ddot{q} + \Omega^2 q = \Phi^T F(t) $$
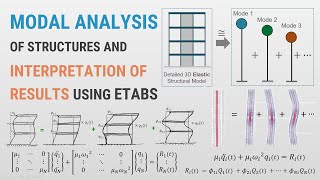
This transformation effectively uncouples the modal equations, permitting independent analysis for each mode. Consequently, by understanding the individual modal responses, engineers can comprehensively analyze the dynamic behavior of 2-DOF systems subjected to varying types of external forces. This method is essential for accurately assessing structural responses in complex systems, particularly in fields such as earthquake engineering.
Youtube Videos




![Lecture 3 Free Vibration Analysis, Examples [ Structural Mechanics ]](https://img.youtube.com/vi/WxLLH1lkHgo/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Forced Vibration Equation
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When subjected to an external force F(t), the system becomes:
Mx¨+Kx=F(t)
Detailed Explanation
When a system experiences an external force, this equation describes how the system will respond. Here, M represents the mass matrix, K is the stiffness matrix, and x is the displacement vector. The equation tells us that the combined effect of the mass and stiffness of the system leads to an acceleration (denoted by x¨) that opposes the external force applied to the system. This is an important principle in dynamics known as Newton's second law, which states that the force acting on an object equals its mass times the acceleration of that object.
Examples & Analogies
Imagine pulling a heavy box on a flat surface. The box won't just move away because you are pulling it; it will also depend on how heavy it is (mass) and how much friction there is between the box and the surface (stiffness). If you apply a steady force to pull the box and the box has significant mass, it will accelerate slowly. This dynamic response is just like the system described by our equation.
Modal Transformation
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Using modal transformation:
x(t)=Φq(t)
where q(t) are the modal coordinates, and Φ is the mode shape matrix.
Detailed Explanation
This equation describes how we can simplify the equation of motion by transforming the original coordinates (x) into modal coordinates (q) using the mode shape matrix (Φ). Each mode shape corresponds to a specific way in which the system can vibrate. By breaking the response into modal coordinates, we can analyze each mode separately, which simplifies our calculations significantly. This transformation is key to reducing complex systems into more manageable forms.
Examples & Analogies
Think of a musical instrument, like a violin. When you play it, the strings vibrate in different modes (fundamental frequency, overtones, etc.). Each mode has a unique sound and frequency. Notably, you can analyze each string's vibration separately to understand how the instrument produces music, just like how we can analyze each mode of the structure’s vibration separately.
Transformed Equation
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The transformed equation:
q¨+Ω2q=ΦTF(t)
Where Ω is the diagonal matrix of natural frequencies.
Detailed Explanation
In this transformed equation, the left-hand side describes the motion of the modal coordinates q in relation to their natural frequencies, represented by Ω. This equation shows that each modal coordinate reacts independently to the transformed external force. The diagonal nature of the matrix Ω indicates that there is no coupling between different modes in this transformed representation, meaning we can analyze them separately rather than as a complex, interconnected system.
Examples & Analogies
Picture a seesaw. When one side goes up, the other side goes down. If we treated the seesaw as separate planks instead of one piece, we could understand how each part moves on its own without affecting the others. This approach simplifies how we analyze its movement, like we simplify the modal analysis in forced vibrations.
Decoupling of Modal Equations
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Each modal equation is uncoupled, allowing individual analysis.
Detailed Explanation
The term 'uncoupled' refers to the fact that, in this modal analysis, each modal equation can be solved independently of the others. This uncoupling arises from the orthogonality of the mode shapes and the nature of the diagonal matrix of natural frequencies. By examining each mode separately, engineers can easily evaluate the response of the system to external forces, which greatly simplifies calculations and predictions regarding the system’s behavior during forced vibrations.
Examples & Analogies
Consider a classroom where each student is learning a different subject—math, science, or history. If their progress does not affect each other, it becomes easier for the teacher to assess how each student is doing individually rather than trying to evaluate them all at once. This is akin to how the modal analysis allows engineers to evaluate each vibration mode separately, simplifying the process of understanding the system's overall response to forces.
Key Concepts
-
Forced Vibration: The dynamic response of systems to external forces.
-
Modal Transformations: Techniques that simplify complex equations of motion.
-
Modal Coordinates: Essential variables enabling individual analysis of modes.
Examples & Applications
A building during an earthquake experiences forced vibrations as it reacts to ground motion.
Using modal analysis, engineers evaluate how parts of a bridge respond individually to wind forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Forced vibration, what a sensation! External forces cause the motion's creation.
Stories
Imagine a tall building swaying during an earthquake—each sway represents different modes reacting to forces applied.
Memory Tools
FAM (Forced, Analysis, Modal) to remember the components of forced vibration analysis.
Acronyms
FEM (Forced Excitation Modal) to remember how external forces affect modes of vibration.
Flash Cards
Glossary
- Forced Vibration
The response of a dynamic system when subjected to external forces.
- Modal Analysis
A technique to analyze the dynamic behavior of structures by examining their natural frequencies and mode shapes.
- Modal Coordinates
Variables that represent the response of modal shapes in a dynamic system.
Reference links
Supplementary resources to enhance your learning experience.
