Numerical Example
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass and Stiffness Matrices
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore how to form mass and stiffness matrices for our 2-DOF system. Can anyone tell me what the mass and stiffness of our system are?

We have two masses, each 1000kg.

That's right! And what about the stiffness values?

The stiffness is 20000 N/m for each spring, with an additional coupling stiffness of 10000 N/m.

Perfect! We can now set up our mass and stiffness matrices as follows: M = [[1000, 0], [0, 1000]] and K = [[30000, -10000], [-10000, 30000]]. Remember this format; it’s essential for the next steps. Now, who can summarize why we need these matrices?

They're needed to analyze the system's dynamic behavior based on the forces involved!

Exactly! These matrices help us articulate the equations of motion.
Solving the Eigenvalue Problem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we need to solve the eigenvalue problem. What does this entail?

We plug the mass and stiffness matrices into the equation det(K - ω²M) = 0!

Excellent! This equation allows us to compute the natural frequencies. Who remembers how to find them?

We determine the values of ω that satisfy the determinant equation.

That's correct! What results do we expect to find, specifically in terms of natural frequencies?

We will find two distinct natural frequencies for our 2-DOF system!

Right! Once we have those frequencies, we can determine the corresponding normalized mode shapes. Remember, these mode shapes describe the system's deformation patterns at those frequencies.
Understanding Modal Superposition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we have our natural frequencies and mode shapes, let’s dive into modal superposition. What is modal superposition’s purpose in dynamic analysis?

It helps us combine individual modal responses to get the total system behavior under dynamic loading!

Exactly! It allows us to handle complex responses by simplifying the dynamic analysis. Can someone describe how we should approach applying modal superposition practically?

We would calculate the modal participation factors and then combine these modal responses.

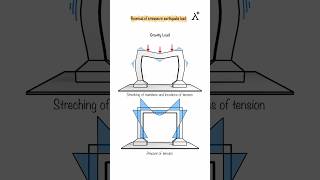
Correct! This approach significantly reduces computational effort, allowing us to effectively analyze our structure's response during seismic events.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The numerical example illustrates the practical application of a 2-DOF system with specified masses and stiffnesses, guiding the reader through forming mass and stiffness matrices, solving the eigenvalue problem, and finding natural frequencies along with their corresponding mode shapes.
Detailed
Numerical Example
In a 2-degree of freedom (2-DOF) system, the behavior of the system can be analyzed using numerical examples to reinforce the theoretical concepts presented earlier in the chapter. This example involves two equal masses and distinct stiffness values:
- Two masses, each weighing 1000kg,
- Two stiffness values of 20000N/m, and a coupling stiffness of 10000N/m.
The analysis will include forming the mass and stiffness matrices, solving for natural frequencies, and corresponding normalized mode shapes. This exercise emphasizes practical understanding of 2-DOF dynamics and the significance of modal analysis in earthquake engineering.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
System Definition
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Consider a 2-DOF system with:
• m1 = m2 = 1000 kg
• k1 = k2 = 20000 N/m, k12 = 10000 N/m
Detailed Explanation
In this numerical example, we are analyzing a two-degree of freedom (2-DOF) system consisting of two masses (m1 and m2), both weighing 1000 kg. Additionally, we have stiffness values: k1 and k2, each equal to 20000 N/m, and a coupling stiffness (k12) equal to 10000 N/m. The system's behavior will be derived from these components, showcasing its dynamic response to external effects.
Examples & Analogies
Imagine two heavy blocks connected with a spring. The mass of each block is like a weight on a balance scale, while the springs represent how tight or loose the connection is between them. Adjusting the stiffness of these springs can change how they respond to being pushed or pulled.
Forming Matrices
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Form the mass and stiffness matrices, solve the eigenvalue problem, find:
• ω1, ω2 (natural frequencies)
• Corresponding normalized mode shapes
• Use modal superposition for dynamic response
Detailed Explanation
To analyze the dynamic behavior of our 2-DOF system, we first need to form the mass matrix (M) and the stiffness matrix (K). The mass matrix will include the masses of the two blocks, and the stiffness matrix will contain the stiffness values and coupling term. Once we have these matrices, we will solve the eigenvalue problem to find the natural frequencies (ω1 and ω2) and the normalized mode shapes associated with each frequency. Finally, we will apply the modal superposition method to predict how the system reacts to dynamic forces.
Examples & Analogies
Think of tuning a musical instrument. The mass matrix is like the weight of the notes, the stiffness matrix represents the tension in the strings, and the natural frequencies are akin to the pitch of each note. Finding the correct frequencies allows us to understand how these notes resonate together in harmony.
Practical Implications
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This exercise reinforces practical understanding of 2-DOF dynamics.
Detailed Explanation
By working through this numerical example, students can practically apply the theoretical concepts of 2-DOF dynamics. It transforms abstract principles into a tangible exercise, helping students to better grasp how a real-world system can be modeled and analyzed for its dynamic properties. This hands-on approach is crucial for engineering students who will later apply these principles in real-world structural dynamics scenarios.
Examples & Analogies
Consider building a playground swing set. You need to know the weight of the kids that will use it (mass), the materials used in its construction (stiffness), and how those factors interact to ensure it’s safe and enjoyable. This example echoes the importance of precisely understanding the dynamics involved to optimize the design.
Key Concepts
-
2-DOF System: Characterized by two independent coordinates required for motion.
-
Mass and Stiffness Matrices: Central elements in formulating the equations of motion for dynamic systems.
-
Natural Frequencies: Frequencies at which the system will oscillate freely.
-
Mode Shapes: Specific patterns that describe how the system deforms at each natural frequency.
Examples & Applications
Consider two masses each weighing 1000kg connected by springs of stiffness 20000N/m, along with a coupling stiffness of 10000N/m; this setup exemplifies a simple 2-DOF system.
In analyzing this 2-DOF system, we derive the mass matrix and stiffness matrix to run an eigenvalue analysis to find the natural frequencies and mode shapes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Two masses sit so still, each a thousand, what a thrill! Springs connect, 'tween them sway, frequencies lead the way.
Stories
Imagine two dancers, each dancing at their own rhythm but connected by an elastic band. As they move, their movements influence each other, creating a beautifully coordinated performance. This is like our 2-DOF system, where each mode affects the overall dynamic behavior.
Memory Tools
M&M's for Mass and Matrix; K for Kinetic Stiffness; Remember: M relates to mass, K relates to how tightly they're bound.
Acronyms
2D-MER
'2 DOF Mass and Eigenvalue Response' to remember the key elements in analyzing a two-degree-of-freedom system.
Flash Cards
Glossary
- Mass Matrix (M)
A matrix that represents the masses in the system and their connection, necessary for dynamic analysis.
- Stiffness Matrix (K)
A matrix representing the stiffness of the springs connecting the masses, crucial for establishing the system's equations of motion.
- Natural Frequency (ω)
The frequency at which the system naturally oscillates when not subjected to any external force.
- Mode Shape (Φ)
A representation of the deformation pattern of a system at its natural frequencies.
- Eigenvalue Problem
A mathematical problem that involves determining the eigenvalues and eigenvectors of a matrix, used to find natural frequencies and mode shapes.
Reference links
Supplementary resources to enhance your learning experience.
