Modal Superposition for Earthquake Analysis
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basics of Modal Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, let's explore modal superposition in earthquake analysis. Can anyone define what we mean by 'modal analysis'?

Is it about breaking down a structure's vibrations into different modes?

Exactly! Modal analysis helps us understand how structures respond in different modes of vibration. Now, why do you think this is important for earthquake engineering?

Because structures react differently during seismic events, and understanding those responses helps us design better.

Well said! By analyzing these modes, we can design structures to be more resistant to earthquakes.

Remember the acronym MARS—Modal Analysis, Responses, and Seismic design. This could help you recall the significance of modal analysis.
Steps in Modal Superposition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s outline the steps in the modal superposition method. Who can tell me one of the first steps?

Finding the mode shapes and natural frequencies?

Correct! After determining the mode shapes (ϕ) and natural frequencies (ω), what's the next step?

Calculating the modal participation factors?

That's right! Those factors tell us how strongly each mode participates in the response under seismic loads. After that, we solve for the modal response (q(t)).

And then we superimpose those responses to get the total displacement?

Exactly! By using the formula $$x(t) = \sum_{i=1}^{2} \phi q_i(t)$$, we can combine the results from each mode. Remember the phrase 'Step by Step,' to recall these steps!
Applications of Modal Superposition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the real-world applications of modal superposition. Why do you think engineers prefer this method when analyzing structures?

It likely simplifies the calculations and makes it easier to analyze complex structures.

Absolutely! It transforms complex dynamic problems into manageable ones by treating each mode independently. Can you think of a specific structure type that benefits from this method?

Maybe tall buildings or bridges since they experience various vibrational modes?

Exactly right! Those structures can have complicated vibrational behaviors, making the modal superposition methodology very insightful.

Remember, 'Modal Matters for Structures'—a catchy phrase to help you keep this application in mind.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the modal superposition method applied in earthquake engineering, which involves calculating modal responses of a structure and then superimposing these responses to represent the total dynamic behavior of the system. It highlights the foundational steps required for effective implementation.
Detailed
Modal Superposition for Earthquake Analysis
In earthquake engineering, the response of structures subjected to seismic ground motion can be efficiently analyzed using the modal superposition method. This approach simplifies complex dynamics by breaking down the system into its modal components.
Key Steps in Modal Superposition:
- Determine the mode shapes (ϕ) and natural frequencies (ω) of the system.
- Calculate modal participation factors (Γ) that quantify the contribution of each mode in response to seismic input.
- Solve for the modal response (q(t)) using the ground motion acceleration (x¨(t)).
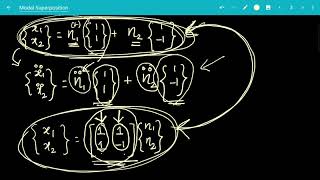
- Finally, compute the total displacement (x(t)) of the structure by superimposing the contributions from each mode:
$$x(t) = \sum_{i=1}^{2} \phi q_i(t)$$
This method effectively transforms the problem into a series of uncoupled single-degree-of-freedom (SDOF) problems, significantly reducing computational effort and complexity. The modal superposition approach is crucial for analyzing the dynamic behavior of modern structures, especially in seismic zones.
Youtube Videos






![22 - Mode-superposition Method of Dynamic Analysis of Structures [Summary]](https://img.youtube.com/vi/WzUbzjix-V8/mqdefault.jpg)

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Modal Superposition Method
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In real-world applications, especially in seismic design, the modal superposition method allows solving the dynamic response of structures using: 1. Calculation of modal responses (SDOF-like response for each mode). 2. Superposition of modal responses to get total system behavior.
Detailed Explanation
The modal superposition method is a technique used to analyze how structures respond to dynamic loads, such as earthquakes. First, the method calculates modal responses, which are individual responses of the system based on single-degree-of-freedom (SDOF) models for each mode of vibration. This simplifies the complex behavior of a multi-degree-of-freedom system into manageable parts. Next, the responses from these modes are combined, or superimposed, to arrive at the overall behavior of the structure under an applied load.
Examples & Analogies
Think of a modal superposition like a music band. Each musician represents a different mode of the structure. When they play their individual parts (modal responses), it might sound disjointed. But when they come together and play as a group (superposition), the music becomes harmonious, representing the total sound of the band.
Steps in the Modal Superposition Method
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Steps: 1. Find mode shapes ϕ and frequencies ω . i i 2. Calculate modal participation factors Γ . i 3. Solve for modal response q (t) using the ground motion x¨ (t). 4. Compute total displacement: x(t)= ϕ q (t) i i i=1
Detailed Explanation
To employ the modal superposition method, several key steps must be followed. First, the mode shapes (the inherent patterns of vibration) and the natural frequencies (how fast each mode vibrates) are determined for the structure. Next, you compute the modal participation factors, which indicate how much each mode contributes to the overall response. After that, each modal response (q(t)) is solved using the equation that incorporates the effect of ground motion (such as during an earthquake). Finally, the total displacement of the structure is calculated by summing the contributions from all the modes, giving us a complete picture of how the structure will move.
Examples & Analogies
Imagine building a house from LEGO. Each piece represents a different mode of the structure. You first identify which pieces (modes) go where (mode shapes), figure out how they fit together (frequencies), and then see how each piece contributes to the overall stability of the house as you add weight (ground motion). Finally, you look at the entire structure to see how it holds up during an earthquake (total displacement).
Significance of Modal Superposition
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This method significantly reduces computational effort compared to solving the full system directly.
Detailed Explanation
One of the major advantages of the modal superposition method is its efficiency. Instead of solving a complex set of equations that describe the full dynamic behavior of a structure under earthquake loading, this method allows engineers to break the problem down into smaller, more manageable pieces. Each mode can be analyzed independently, significantly simplifying the calculations. As a result, this approach saves time and resources, making it easier to perform seismic analyses for different structures.
Examples & Analogies
Think of solving a jigsaw puzzle. If you try to put together the whole puzzle at once, it can be overwhelming. But if you focus on sorting out the edge pieces first (the modal responses) and then fill in the center pieces afterwards (superposition), the task becomes much simpler and faster to complete.
Key Concepts
-
Modal Analysis: A technique for understanding a structure’s dynamic response.
-
Modal Superposition: The method used to combine the responses from different modes.
-
Modal Participation Factors: Determines how each mode contributes to the overall response.
-
Natural Frequencies: The frequencies at which structures oscillate naturally.
-
Mode Shapes: The specific pattern of vibration for each natural frequency.
Examples & Applications
In the design of a skyscraper, modal superposition allows engineers to assess how its multiple vibrations during an earthquake can be combined to evaluate the building's overall response.
For a bridge exposed to seismic waves, modal analysis helps in understanding how each section of the bridge vibrates and interacts, aiding in design improvements.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In earthquake tales, we break it down, modal methods make us wear the crown!
Stories
Imagine a city where each building sways like a dancer. Using modal superposition, engineers predict each dancer's moves to ensure they don't collide!
Memory Tools
Think 'MPS' - Modes, Participation, Superposition - to recall the key steps in modal superposition.
Acronyms
Remember 'MAPS' - Modal shapes, Analysis, Participation factors, Superposition for earthquake analysis.
Flash Cards
Glossary
- Modal Analysis
A technique to analyze the vibration modes of structures, used to predict their dynamic response.
- Modal Superposition
A method for calculating the total dynamic response of a structure by combining the effects of individual vibrational modes.
- Modal Participation Factor (Γ)
A coefficient that indicates how much a specific mode contributes to the overall response of the structure.
- Natural Frequency (ω)
The frequency at which a system naturally oscillates when not disturbed by external forces.
- Mode Shape (ϕ)
The shape of the oscillation of a system corresponding to a specific natural frequency.
Reference links
Supplementary resources to enhance your learning experience.
