Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Box Models and Mixing Height
Unlock Audio Lesson
Today, we are going to explore box models, which are crucial for understanding how pollutants disperse in the air. Can anyone tell me what they think a mixing height is?
I think it’s the height at which pollutants get mixed in the atmosphere?
Exactly! The mixing height is where the environmental lapse rate meets the adiabatic lapse rate. This is essential as it determines how pollutants are dispersed. Let’s remember it by the acronym M.H.I.T: Mixing Height Influences Transport.
What does adiabatic lapse rate mean?
Great question! The adiabatic lapse rate refers to the rate at which temperature decreases with altitude in a rising air parcel, assuming no heat is lost. Can anyone tell me what stability means in this context?
Is it how resistant the air parcel is to rising?
Exactly right! Stability is a measure of how an air parcel behaves when displaced upward. At the end of today, it’s important to understand how mixing height helps us predict pollutant levels.
The Role of Stability and Adiabatic Processes
Unlock Audio Lesson
Now, let’s dive deeper into stability. Why is it important for modeling pollutants in air?
Because stable air doesn’t mix well, right?
Correct! Stable atmospheres trap pollutants close to the ground. Can someone explain what we mean by an adiabatic process?
It means there is no heat exchange when the air rises?
Absolutely! The air parcel expands and cools without heat exchange, influencing its density and buoyancy significantly. Remember, in an adiabatic process, it’s quick—essentially insulated from external heat sources.
How does this connect to potential temperature?
Great segue! Potential temperature helps in comparing temperatures at different pressures. It’s like normalizing data to make predictions easier!
Defining the Transport Model
Unlock Audio Lesson
Let’s discuss how we define a transport model for the concentration of pollutants. Why do we use differential equations?
To understand how concentration changes over time and space?
Precisely! In a box model, we look at accumulation rates, flow rates, and dispersion rates. Can someone recite what A.C.F.D stands for?
Accumulation, Concentration, Flow, and Dispersion?
Exactly! These concepts help us write equations that describe pollutant behavior. Each term in these equations represents crucial processes we identified. Let’s connect this to practical scenarios—how can you apply this knowledge to predict concentrations?
By calculating how far someone standing downwind from a source might be exposed to pollutants?
Indeed! This practical application emphasizes why understanding box models is essential for air quality management.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamental principles of box models used in environmental studies for the transfer of pollutants in the air. Key concepts include mixing height, stability in the atmosphere, and deriving equations for pollutant concentration as a function of spatial and temporal variables.
Detailed
Introduction to Box Models
In this section, we delve into box models utilized for monitoring and analyzing pollutant transfers in air. Box models serve as powerful tools for estimating the movement and concentration of pollutants based on various physical processes. One critical aspect discussed is mixing height, which is influenced by atmospheric stability—a concept describing how rising air parcels behave with temperature gradients in the lower atmosphere.
Key Concepts:
- Mixing Height: Defined as the height where the environmental lapse rate intersects with the adiabatic lapse rate, influencing air pollution dispersion.
- Stability: Refers to the behavior of air parcels when they rise from the Earth's surface, determined by temperature and the environmental lapse rate.
- Adiabatic Process: This is the assumption where no heat is exchanged with the environment during the upward movement of air parcels, thus influencing their temperature and density changes.
The section also covers mathematical formulations including the definition of potential temperature and the derivation of adiabatic lapse rate (B3), which is an essential element in atmospheric science.
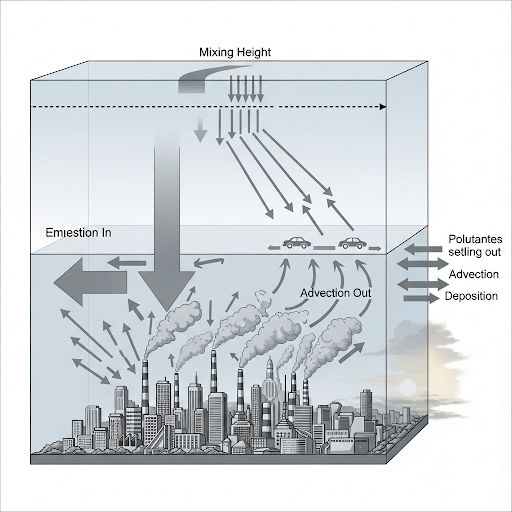
By creating a generalized transport model that considers accumulation, flow, and dispersion, we can begin to predict pollutant concentration over time using various equations derived from Fick’s law of diffusion. The discussion points towards practical modeling and calculations necessary for evaluating air quality and exposure scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Concept of Box Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we were looking at box models for pollutant transfers in air. So, essentially this is a generic box model for air. The processes that we are considering in the box include advection, dispersion, reaction exchange and all that.
Detailed Explanation
Box models are simplified representations used to understand how pollutants transfer through the air. They consider various processes like advection (pollutant transport due to the movement of air), dispersion (spreading out of pollutants), and reaction exchanges (chemical reactions that can occur involving pollutants). This helps in predicting how pollutants behave in the air.
Examples & Analogies
Think of a box as a room with open windows. If someone starts spraying air freshener in the room, the fresh scent will spread throughout the room (dispersion) while the wind from the open windows carries some of that scent outside (advection). Understanding how this process works can help us determine how long the scent will last in the room.
Stability in Atmospheric Behavior
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the specific problem for air is that the height is not very well defined, so we look at what is called as a mixing height and mixing height depends on concept called stability and stability is function of temperature in the lower atmosphere.
Detailed Explanation
In the atmosphere, the concept of mixing height is essential because it represents the altitude at which the air mixes. This height is influenced by stability, which refers to how air parcels behave when they rise or fall. Stability calculations are based on temperature gradients in the lower atmosphere, affecting how pollutants mix and disperse in the air.
Examples & Analogies
Imagine a hot air balloon. When the air inside the balloon is heated, it wants to rise because it’s lighter than the surrounding cooler air. However, if the surrounding air is stable (meaning it’s cooler as you go higher), the balloon might not go up very much. In a similar way, atmospheric stability affects how high pollutants can rise and disperse in the air.
Adiabatic Process and Lapse Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The lapse rate represented by Gamma, the adiabatic lapse rate is given as -0.0098 centigrade per kilo per meter or 9.8 centigrade per kilometer. This is the adiabatic lapse rate.
Detailed Explanation
The adiabatic lapse rate is the rate at which temperature decreases with an increase in altitude for a parcel of air that is rising without exchanging heat with its surroundings. It is important for understanding how temperature changes in the atmosphere, influencing weather patterns and pollutant distribution.
Examples & Analogies
Consider a mountain trek where temperature drops as you climb higher. As you go up, you feel it getting cooler because the air is expanding and cooling without absorbing heat from anywhere (adiabatic process). Understanding this concept helps us predict how pollutants might behave as air rises and cools in the atmosphere.
Potential Temperature
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There is another term called potential temperature is defined like this theta equals T0. This is the temperature corrected to particular pressure, so the pressure with reference to sea level pressure.
Detailed Explanation
Potential temperature is a modified temperature value that accounts for changes in pressure. This is significant because it allows meteorologists to compare temperatures at different altitudes on a consistent basis, improving our understanding of atmospheric stability and pollutant behavior.
Examples & Analogies
Think of potential temperature as comparing the temperature of different liquids in sealed containers at different heights in a stack. Even if a liquid at the top is cooler due to lower pressure, potential temperature lets us understand its energy state as if it were at the same height as the others.
Mixing Height Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We also looked at this concept of mixing height, mean mixing height as the place where the intersection of the environmental lapse rate and adiabatic lapse rate happens.
Detailed Explanation
The mean mixing height is crucial in understanding air pollution dispersal. It is the altitude at which the temperature of rising air parcels becomes equal to the surrounding air, leading to effective mixing of pollutants. This intersection influences how pollutants disperse in the atmosphere.
Examples & Analogies
Imagine pouring cream into coffee. Initially, the cream sits on top because it's denser, but as you stir, it mixes throughout the coffee. Similarly, the mixing height determines where in the atmosphere the pollutants (like cream) will effectively mix with the surrounding air (like coffee).
Understanding Plume Shapes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There are different kinds of plume shapes that can be expected based on variations such as environmental lapse rate and plume source height.
Detailed Explanation
Plume shapes depict the distribution of pollutants as they exit a source and interact with atmospheric conditions. The shape can vary depending on several factors including wind patterns, temperature differences, and source height, which helps in predicting pollutant dispersion.
Examples & Analogies
Consider how smoke from a chimney disperses. On a still day, the smoke rises straight up, forming a narrow plume. On a windy day, it may spread out wide, creating a broader plume shape. Understanding these shapes allows us to predict how far pollutants might travel from a source.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mixing Height: Defined as the height where the environmental lapse rate intersects with the adiabatic lapse rate, influencing air pollution dispersion.
-
Stability: Refers to the behavior of air parcels when they rise from the Earth's surface, determined by temperature and the environmental lapse rate.
-
Adiabatic Process: This is the assumption where no heat is exchanged with the environment during the upward movement of air parcels, thus influencing their temperature and density changes.
-
The section also covers mathematical formulations including the definition of potential temperature and the derivation of adiabatic lapse rate (B3), which is an essential element in atmospheric science.
-
-
By creating a generalized transport model that considers accumulation, flow, and dispersion, we can begin to predict pollutant concentration over time using various equations derived from Fick’s law of diffusion. The discussion points towards practical modeling and calculations necessary for evaluating air quality and exposure scenarios.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a pollutant is released from a site, understanding the mixing height will inform how high the pollutant can rise before being dispersed.
-
In urban areas, stable atmospheric conditions may lead to higher pollution levels than in turbulent conditions, highlighting the importance of stability in air quality assessment.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the sky, where air tags, mixing height helps as it drags.
📖 Fascinating Stories
-
Imagine a balloon rising silently in the sky, its temperature dropping only because it climbs higher, much like pollutants escaping the grip of a city’s warmth.
🧠 Other Memory Gems
-
Remember M.H.I.T: Mixing Height Influences Transport.
🎯 Super Acronyms
S.A.P.E
- Stability Affects Pollutant Exposure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Box Model
Definition:
A simplified representation of pollutant dispersion in the environment, considering various physical processes.
-
Term: Mixing Height
Definition:
The height in the atmosphere at which the environmental lapse rate intersects with the adiabatic lapse rate, signifying where pollutants become mixed.
-
Term: Stability
Definition:
A measure of an air parcel's behavior regarding its ability to rise and mix based on temperature gradients.
-
Term: Adiabatic Process
Definition:
A thermodynamic process where there is no heat transfer to or from the air parcel as it rises.
-
Term: Potential Temperature
Definition:
The temperature of an air parcel corrected for its pressure with respect to sea level, aiding in comparisons across altitudes.
-
Term: Adiabatic Lapse Rate
Definition:
The rate of temperature change in an air parcel as it rises or descends after being displaced adiabatically.