Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid at Rest
Unlock Audio Lesson
Today, we will focus on fluids in a state of rest. Can anyone tell me what happens to the velocity of a fluid when it is at rest?
The velocity is zero.
Exactly! Since the velocity is zero, we can ignore velocity gradients and shear stress. How does this simplify our analysis?
We only need to consider the pressure field!
Exactly! The pressure field becomes the primary concern when analyzing fluids at rest.
Understanding Pressure and Its Distribution
Unlock Audio Lesson
Now, let’s talk about how pressure varies in fluids at rest. Can anyone explain how pressure changes with depth?
Pressure increases with depth due to the weight of the fluid above it.
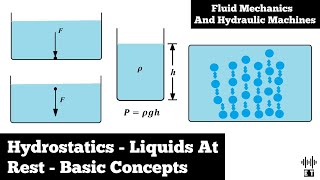
Correct! This is foundational in hydrostatics. The equation we often use is P = P₀ + ρgz. Who can explain what each term represents?
P is the pressure, P₀ is the atmospheric pressure, ρ is the fluid density, g is the acceleration due to gravity, and z is the depth.
Exactly! Great explanation. This formula helps us understand pressure distribution in various applications.
Pascal's Law
Unlock Audio Lesson
Let’s move on to Pascal's law. Who can summarize what Pascal's law states?
It states that the pressure applied to a confined fluid is transmitted undiminished in all directions.
Exactly! This law is crucial in many hydraulic systems. Can anyone give me a real-world example where Pascal's law applies?
In hydraulic brakes for cars!
Right! Well done. This principle ensures that the force applied at one point is transmitted equally through the fluid.
Applications in Real Life
Unlock Audio Lesson
Now, let’s connect this to real life. How do we apply these concepts when designing a dam?
We need to calculate the pressure acting on the dam at various depths!
Exactly! Knowing how pressure acts on a dam helps in its design to withstand forces. Any other application that comes to mind?
Oil tanks! We need to know the pressure exerted on the tank walls.
Perfect example! These applications illustrate the importance of understanding fluid at rest.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the behavior of fluids at rest, highlighting the importance of pressure fields, Pascal's law, and the absence of shear stress. Key concepts include hydrostatic pressure distributions and their applications in designing structures like dams and tanks.
Detailed
In this section on the basic concepts of fluid at rest, we delve into hydrostatics, which governs the properties and behaviors of static fluids. When fluids are at rest, we can simplify our analysis, primarily focusing on pressure fields. Essential topics include the concept of pressure as a function of position, the implications of having zero shear stress, and how pressure is distributed in static fluids according to Pascal's law. Practical applications such as the operation of a barometer and understanding the capillary effect are also discussed. Throughout this lecture, we utilize mathematical approximations, such as the Taylor series, to express pressure changes in terms of spatial variables. The significance of these concepts is reinforced with examples that aid in understanding real-world applications within civil engineering, particularly in constructing dams and storage tanks.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now.
Detailed Explanation
A fluid at rest refers to a state where there is no movement of fluid molecules; hence, the velocity vectors are zero. When we analyze fluids, we often need to consider aspects like pressure, velocity, and density. However, under rest conditions, the analysis is drastically simplified because we don't need to worry about velocity or velocity gradients.
Examples & Analogies
Imagine a glass of water on a table. The water is not moving, indicating a stable fluid at rest. If you were to look at this water closely, you would find that the pressure at any point in the water is constant and only influenced by the weight of the water above it.
Behavior of Pressure in a Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means when fluid is at rest conditions only we need to know it how the pressure variations is going over these fluid domains. That is what the simplified problems.
Detailed Explanation
In a fluid at rest, pressure changes with depth due to the weight of the fluid above exerting force downwards. This can be described using the hydrostatic pressure equation, where the pressure increases linearly with depth. This means that the deeper you go into the fluid, the greater the pressure you will experience.
Examples & Analogies
Consider diving into a swimming pool. As you swim deeper beneath the surface, you feel the increased pressure on your ears. This is a direct result of the weight of the water above you and exemplifies how pressure in a fluid at rest is affected by depth.
Effects of Gravity on Fluid Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress.
Detailed Explanation
Newton's second law indicates that force is required to change the motion of an object. In a fluid at rest, since there is no movement, there are no shear stresses acting on the fluid. We can only consider vertical forces such as gravity, which acts uniformly downward.
Examples & Analogies
Think about the kitchen sponge filled with water. When the sponge stands still, the water remains in place due to the force of gravity acting on it; however, if you squeeze the sponge, you start to see shear stress as the fluid moves. In rest, however, the pressure only balances forces due to gravity.
Control Volume and Fluid Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What the two forces we have? The gravity force and the force due to the pressure distribution.
Detailed Explanation
In analyzing a control volume of fluid at rest, we primarily focus on two forces: the gravitational force acting on the volume of fluid and the force due to pressure acting on the walls of that control volume. When in equilibrium, these forces balance each other.
Examples & Analogies
Envision a parked car. It remains stationary because the gravitational force pulling it downwards is counterbalanced by the normal force exerted by the ground. Similarly, in fluids at rest, the gravitational force is balanced by pressure forces acting on any submerged surfaces.
Examples of Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example, if you take this dam, which is 100-meter-high and we have a reservoir, let you consider this is what 90 meter height from the bottom.
Detailed Explanation
Analyzing a dam is a classic example of fluid at rest. Here, the pressure exerted by the water in the reservoir increases with depth. Engineers must account for this pressure when designing the dam, ensuring it can handle the forces acting upon it.
Examples & Analogies
Imagine a large reservoir of water behind a dam. The water resting against the dam creates significant pressure at its base. Engineers design the dam to withstand this pressure much like how a strong foundation is needed under a tall building to support its weight.
Rigid Body Motion of Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Second thing is that fluid act as a rigid body motions. Let us take an example here that I have a tank which is a half filled liquid is there.
Detailed Explanation
When a tank containing fluid is accelerated, the fluid can behave like a rigid body. In this case, even though the fluid is at rest relative to the tank, the shape of the surface changes due to the acceleration. Understanding this concept is crucial in applications involving moving fluids, such as in transport and storage.
Examples & Analogies
Think of a car making a sharp turn. If you have a cup of water on the dashboard, the water will slosh to one side when the car turns. Inside the turning car, the water is still at rest relative to you, but its surface appears tilted due to the car's acceleration.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: The study of fluids at rest impacts pressure and fluid behavior.
-
Pascal's Law: It states that pressure changes in a confined fluid are transmitted equally in all directions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The pressure at the base of a dam increases with the height of water above it, crucial for structural design.
-
In hydraulic systems, force applied at the brake pedal is transmitted through the fluid to stop the vehicle.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fluid at rest, pressure grows, / The deeper you go, the more it shows.
📖 Fascinating Stories
-
Imagine a tall glass of water. As you dive deeper, the pressure builds around you. Each centimeter down adds weight from above, just like layers in a cake!
🧠 Other Memory Gems
-
P.A.R.E - Pressure Always Rises with Elevation (depth).
🎯 Super Acronyms
P.A.S.C.A.L = Pressure Applied to a Static Cavity Acts in All Directions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The branch of fluid mechanics that studies fluids at rest.
-
Term: Pressure
Definition:
The force exerted per unit area within a fluid.
-
Term: Pascal's Law
Definition:
A principle stating that changes in pressure applied to an enclosed fluid are transmitted throughout the fluid.
-
Term: Gauge Pressure
Definition:
The pressure relative to atmospheric pressure.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above.