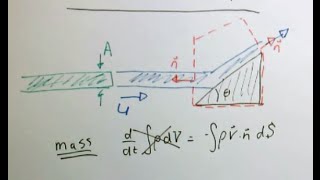
Control Volume Considerations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome everyone! Today we’ll start discussing control volumes. Can anyone explain what a control volume is?

Is it like a defined space where we analyze fluid behaviors?

Exactly! A control volume is a fixed region in space where we analyze fluid motion and forces. Remember this acronym: C.V. - Control the Volume!

Why do we need to focus on control volumes?

Control volumes help us apply the conservation laws—mass, momentum, and energy, which are critical in fluid mechanics. What happens to fluid in our control volume under static conditions?

There are no velocity gradients, and shear stress is absent!

Exactly, well done! Let’s remember: 'Rest equals no shear'.
Hydrostatic Pressure
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s move on to hydrostatic pressure. How does pressure behave in a fluid at rest?

Pressure increases with depth because of the weight of the fluid above.

That's correct! The relationship can be expressed as P = P0 + ρgh, where P0 is the surface pressure. Can anyone remember what ρ and g stand for?

ρ is the density of the fluid, and g is the acceleration due to gravity.

Good! Let’s use the mnemonic 'Pressure Mills Create Height' to remember pressure’s dependence on density and height.

So for fluids at rest, it's only pressure we’re concerned with?

Yes, in static conditions, we focus solely on pressure, making our analysis significantly simplified. Can anyone think of a practical example?

Dams! The pressure below the water level is essential for structural design.

Great example! Dams are indeed a primary application of hydrostatic principles.
Pascal's Law
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we’ll discuss Pascal's Law. Who can explain what this law states?

It states that pressure applied to a confined fluid transmits equally in all directions.

Exactly! Remember, *Equally Everywhere* for Pascal's Law. This principle is crucial for understanding fluid systems like hydraulics. How do we apply this in control volumes?

It helps us calculate forces on various surfaces within the control volume.

Perfect! And can anyone recall how we derive these calculations?

By setting up force balance equations and applying the assumption of hydrostatic pressure.

Exactly, and that brings us to how we calculate pressure gradients. Understanding this allows us to analyze many fluid scenarios.
Applications of Hydrostatic Pressure
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s conclude with applications of hydrostatic principles. What are some real-world instances where we use these concepts?

Designing reservoirs and oil tanks!

Yes! Additionally, we find these in determining pressure in various containers. How might we calculate pressure at a given depth in a tank?

Using P = ρgh!

Excellent! Always remember, knowing the fluid density and height contributes greatly to efficiency in design and functionality.

And we can visualize this with real life objects like a water slide!

Exactly! Let’s recap: Control volumes and hydrostatic principles are vital for accurately modeling fluid behavior in practical situations.
Taylor Series in Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s explore using Taylor series for approximating pressure fields. Does anyone know how we apply Taylor series in this context?

We can use it to approximate values at various points using known values?

That's right! It helps us make complex calculations more manageable. Remember, 'Small steps to big data' As we can neglect higher-order terms often. Anyone wants to walk us through the series?

I think it's about evaluating first derivatives at known points and neglecting the smaller terms.

Exactly! This is crucial in scenarios where precision is key. Understanding these approximations helps in resolving real-world fluid calculations effectively.

So, it’s about simplifying complex scenarios, right?

Exactly. Taylor series is a powerful tool that ensures accuracy in approximating fluids under static conditions. Great discussion today, everyone!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the concepts of control volumes and hydrostatics, highlighting key principles such as Pascal's law, pressure distributions, and their applications in practical scenarios like dam design and fluid tanks. Understanding these fundamental ideas allows for better analysis of fluid behavior when at rest.
Detailed
Control Volume Considerations
This section delves into the essential concepts of hydrostatics and control volumes in fluid mechanics. When dealing with fluids at rest, the fluid dynamics simplifies significantly. The key focus here includes:
- Hydrostatic Conditions: In the hydrostatic state, the velocity gradients vanish, leading to no shear stress in the fluid. Instead, the focus shifts to pressure fields and how these pressures change with depth and other variables. The fundamental equation, derived from Pascal's law, shows that pressure increases with depth due to the weight of the fluid above.
- Pascal's Law: This foundational law states that pressure exerted on a fluid in a closed container transmits equally in all directions. This principle is crucial when analyzing forces acting on control volumes or fluid elements.
- Applications of Hydrostats: The section discusses the implications for applications such as dam design and how the pressures from the fluid can be forcefully equated to understand structural effects. Notably, pressure variations can be calculated using differential relationships among variable pressures at different points.
- Taylor Series Approximation: It also introduces the application of Taylor series in approximating pressure fields using known values at specific locations. This approximation helps simplify complex calculations in practical problems.
Overall, understanding these concepts not only aids in solving fluid mechanics problems but is also vital for engineers and scientists when dealing with structures influenced by fluid pressures.
Youtube Videos






![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fluid at Rest Simplified Concepts
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now.
Detailed Explanation
When we discuss fluids at rest, we examine situations where the fluid does not flow or change position, leading to simplified mathematical modeling. At rest, the velocity of fluid particles is zero. Because there is no movement, we only need to focus on how pressure varies within the fluid. In this simplified scenario, we can ignore the effects of velocity and temperature changes.
Examples & Analogies
Think of a glass of water standing still on a table. The water is not moving, so we don’t have to worry about any currents or ripples affecting its pressure. We only need to be concerned with how much pressure pushes down from the water above and how that pressure influences the glass.
Forces on a Control Volume
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress.
Detailed Explanation
In fluid mechanics, when we analyze forces acting on a control volume, we note that with fluid at rest, shear stress vanishes because the fluid isn't moving. Hence, the main forces acting within the control volume are due to pressure and gravity. In simple terms, if you consider a bottle filled with water standing still, the only forces at play are the weight of the water and the pressure exerted on the walls of the bottle by that water.
Examples & Analogies
Imagine a swimming pool. When you jump into the pool, the water moves and creates waves and pressure differences. But if the pool is filled and no one is in it, the water simply exerts pressure against the pool walls and the bottom, and there are no waves or currents. This is similar to how forces balance out when the fluid is at rest.
Application of Hydrostatic Concepts
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So that is the very easy problems what we have now. And what the two forces we have? The gravity force and the force due to the pressure distribution.
Detailed Explanation
When analyzing fluids at rest, we primarily consider two forces: gravity and pressure distribution. The pressure distribution is influenced by the fluid's column above each point. Essentially, the deeper you go into the fluid, the higher the pressure due to the weight of the fluid above. For example, at the base of a dam, the water pressure is significantly higher than at the surface. This pressure must be calculated to ensure the dam can withstand the force without failing.
Examples & Analogies
Consider a bathtub filled with water. The water exerts pressure on the bottom of the tub due to the weight of the water above it. The deeper you go (like having more water in the tub), the more pressure you feel against the bottom. This is why when you try to dive deep in a pool, you'll feel the pressure on your ears—it's the water above pushing down.
Pascal's Law
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now whenever I am talking about that I am looking for a pressure field as the fluid is at rest. So basically I am looking at the pressure is a function of the positions.
Detailed Explanation
Pascal's Law asserts that in a fluid at rest, pressure applied to any part of the fluid is transmitted equally in all directions. This principle helps us understand how pressure changes across different points within the fluid and allows us to calculate how the pressure influences forces acting on surfaces within the fluid. By analyzing the pressure functions based on depth, we can derive crucial engineering applications, such as designing hydraulic systems.
Examples & Analogies
Think of squeezing a balloon filled with water. When you apply pressure on one end of the balloon, the water moves and transmits that pressure across the balloon evenly, causing it to bulge out on the opposite end. This illustrates how pressure operates uniformly throughout the mass of the fluid.
Key Concepts
-
Control Volume: Crucial for applying fluid analysis.
-
Hydrostatic Pressure: Key in understanding fluid behavior at rest.
-
Pascal's Law: Fundamental in analyzing pressures in fluid systems.
-
Taylor Series: A technique for simplifying complex pressure calculations.
Examples & Applications
Pressure calculation at different depths in a dam, demonstrating how hydrostatic pressure works.
Using Pascal's Law in hydraulics to explain force transmission in brake systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
"Pressure grows, the deeper you go, under the water's weight, let it flow!"
Stories
Imagine a diver going deeper; the pressure increases as water weights down, just like how a pile of books becomes heavier at the bottom.
Memory Tools
Use 'PHD' to remember Pressure, Height, Density for hydrostatic pressure calculations.
Acronyms
C.V.P. - Control Volume Pressure, helps remember the role of pressure in control volumes.
Flash Cards
Glossary
- Control Volume
A fixed region in space where fluid motion and forces are analyzed.
- Hydrostatic Pressure
The pressure exerted by a fluid at rest due to the weight of the fluid above it.
- Pascal's Law
A principle stating that pressure change occurs uniformly in a confined fluid at rest.
- Taylor Series
A mathematical series used to approximate values of functions based on their derivatives.
- Static Condition
A state where the fluid is at rest, resulting in no shear stress.
Reference links
Supplementary resources to enhance your learning experience.
