Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid at Rest
Unlock Audio Lesson
Welcome everyone! Today, we’re discussing hydrostatics, a field focused on fluids at rest. Who can tell me what happens to fluid behavior when it is not in motion?
I think the pressures remain consistent without movement?
Exactly! When a fluid is at rest, its velocity is zero, which means there are no velocity gradients and consequently, no shear stress. This is key in our discussions.
So pressure is the only variable we need to consider?
Correct! We primarily focus on how pressure varies within the fluid’s domain. Remember the acronym **P-V-T** — Pressure, Velocity, Temperature — but here, velocity and temperature are constant.
Why do we need to know about pressure distribution in these scenarios?
Great question! Understanding pressure distribution allows us to design structures like dams safely. Let’s move on to Pascal’s Law.
Pascal's Law
Unlock Audio Lesson
Pascal's Law states that in a fluid at rest, pressure applied at any point is transmitted in all directions. Can someone illustrate this with an example?
If I add pressure at one point in a large container, it affects all points in the container?
Excellent! This uniform pressure transmission is fundamental in hydraulics. If we think of an oil tanker, how does that relate?
The pressure exerts against the walls of the tank evenly!
Right! Thus, when designing the tank, we need to account for these pressure forces. Remember: **P-tank** for Pressure in tanks!
Applications of Fluid at Rest
Unlock Audio Lesson
Let’s apply what we learned! How do we use pressure measurements in dam construction?
We need to know how much water pressure pushes against the dam at different levels.
Exactly! This pressure helps engineers ensure the dam's integrity. What about capillary effects in fluids?
The water rises in small tubes due to surface tension, right?
Correct! The interplay of surface tension and hydrostatic pressure allows for these phenomena. Keep in mind, **H-A-C** for Hydrostatic Applications and Capillarity!
Mathematical Approximations in Hydrostatics
Unlock Audio Lesson
Now, let’s discuss how we can use Taylor series to approximate pressure variations. What do we gain from this?
It helps to simplify our calculations for pressure differences!
Exactly! We ignore higher-order terms because they become negligible. Can anyone share how this is practical in fluid assessments?
In large systems, we can simplify the models, making them easier to analyze without losing much accuracy!
Great application! So remember **T-S-A** for Taylor series in Approximation!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores hydrostatics, detailing how fluids at rest behave and the principles governing pressure distribution in static fluids. It covers Pascal's Law, pressure forces, and provides practical implications, illustrated with examples like dams and tanks. Additionally, it addresses pressure approximations using Taylor series and introduces key definitions in fluid mechanics.
Detailed
Detailed Summary of Fluid at Rest
This section delves into the concept of hydrostatics, which studies fluids that are not in motion. It begins by defining crucial terms such as pressure and its variations in static fluids. Various properties of fluids at rest, including density, temperature, and pressure, are analyzed, highlighting that when fluid is at rest, the velocity vectors are zero, leading to no shear stress. This understanding is foundational in several engineering applications such as dam and tank design.
Key concepts introduced include:
- Pascal's Law, which states that in a fluid at rest, pressure exerted at any point within the fluid is transmitted uniformly in all directions.
- The conditions of equilibrium for fluid elements, allowing us to derive pressure distributions mathematically.
- The applications of hydrostatics in real-life scenarios, particularly in structural designs involving liquids like water or oil.
The section also discusses using the Taylor series to approximate pressure fields by neglecting higher-order terms, which simplifies the analysis of pressure variations across distances. This simplification is particularly useful when evaluating systems where precise measurements are impractical due to small pressure differences.
In conclusion, a solid grasp of these concepts is critical in engineering disciplines focused on fluid dynamics and static stability.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now. Like as I said it any fluid flow problems we look at either the pressure field, the velocity field, or the density and temperature field. When the fluid is rest now, very simply way the velocity vectors becomes zero and if I consider incomprehensible the density is a constant and if the temperature is not very much I need not need a thermodynamics first laws to define the problems. Then only the left is that the pressure field.
Detailed Explanation
When we discuss fluid at rest, we mean that the fluid isn't moving. In this case, all the fluid's velocities are zero, which simplifies our analysis. Since the density of the fluid is constant in incompressible fluids and the temperature changes are negligible, we primarily focus on how pressure varies throughout the fluid. This understanding helps us analyze problems involving fluids without complexity from velocity or changes in density.
Examples & Analogies
Think of a glass of water sitting on a table. The water is at rest; it doesn't flow, and the surface is calm. In this scenario, the only forces at play are the pressure from the weight of the water above and the atmospheric pressure around it. This setup allows us to easily measure and calculate the water pressure at different depths.
Pressure Forces in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress. So when a fluid is at rest, there is no shear stress acting on that. So you can take a surface or take a control volume. Over that control surface you can define it the shear stress components become zero. That is very simplified now that any control volume you consider it over that control volume surface as the fluid is at rest conditions, there is no shear stress acting on the control surface. So that is the very easy problems what we have now.
Detailed Explanation
Without motion, fluids don't have velocity gradients, which eliminates shear stress from the equations. In simple terms, shear stress is the force that causes layers of fluid to slide past one another, but with no movement, this stress does not exist. Thus, when we analyze a control volume—an imaginary box that contains fluid—we find that the only significant forces we need to consider arise from the pressure within the fluid and any external forces like gravity.
Examples & Analogies
Imagine a thick syrup resting in a jar. Because it's not moving, the syrup doesn't exert shear stress in the traditional sense; rather, it's just exerting pressure downwards due to the weight of the syrup. If you try to tilt the jar, you'll notice the syrup remains where it is, demonstrating the lack of shear stress.
Forces Acting on a Fluid Element
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And what the two forces we have? The gravity force and the force due to the pressure distribution. So the whatever the pressure distribution forces that what is equate with the gravity force. Very simple things now, and since is a fluid is at the rest, so you can say that there is no mass flux is coming into the any control volumes or the momentum flux or no external work done it. So this is the what the simplified case.
Detailed Explanation
When considering fluids at rest, we examine two primary forces: the force of gravity acting downwards and the pressure forces acting on the surface of the fluid. In a state of equilibrium (like when water is still in a dam), these forces counterbalance each other. Since there's no movement, mass isn't flowing in or out, and there’s no additional work being done on the system, leading to this simplified analysis.
Examples & Analogies
Think about a swimming pool. The water is at rest, and the pressure at any point in the pool is balanced by the weight of the water above it. As you go deeper, the pressure increases due to the added weight of the water above, but the pool's stillness means all the forces are relatively simple to understand and calculate.
Applications: Designing Structures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Like for example, if you take this dam, which is 100-meter-high and we have a reservoir, let you consider this is what 90 meter height from the bottom. That is what the water levels is 90 meter from the bottom. And you can understand it because of these in the reservoirs the fluid is at the rest conditions and that rest condition exerting the pressures on these surface.
Detailed Explanation
In engineering, understanding how fluid pressure works is crucial for designing structures like dams. For example, a dam holds a large volume of water, and the pressure exerted by this water changes with depth. By calculating the pressure due to the 90 meters of water, engineers can determine the stress on the dam’s walls and ensure it does not fail.
Examples & Analogies
Consider filling a balloon with water. The deeper you go into the balloon (the more water you add), the stronger the pressure feels at the bottom from the column of water pushing down. This principle is the same for dams—the deeper the water, the more pressure there is against the dam wall, and engineers must factor this into their designs to ensure safety.
Hydrostatics and Rigid Body Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Second thing is that fluid act as a rigid body motions. Let us take an example here that I have a tank which is a half filled liquid is there. Let us consider it may have water and this tank is accelerated with a constant acceleration a. As you start accelerating this tank with a constant acceleration a, you can understand it, this free surface is going to change it.
Detailed Explanation
When we accelerate a tank filled with liquid, the liquid surface will adjust to maintain equilibrium. Even though the tank moves, the behavior of the fluid can be analyzed as if it were a rigid body—this means we can still apply hydrostatic principles. Thus, we can find out the new height of the liquid surface when the tank is in motion without complexity from shear forces since there are no gradients in velocity.
Examples & Analogies
Imagine you're in a car that suddenly accelerates. If you have a cup of water in hand, the water will tilt back as you accelerate. Though the car moves, the surface of the water remains flat, showcasing that the fluid behaves as if it's part of a rigid system, making hydrostatic calculations still valid.
Pressure Field in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
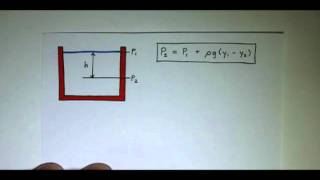
Now whenever I am talking about that I am looking for a pressure field as the fluid is at rest. So basically I am looking at the pressure is a function of the positions. Time is not there, as the fluid is at rest condition.
Detailed Explanation
Pressure in a fluid at rest is dependent on the positions within the fluid instead of time. This means we can analyze how pressure changes with depth or across different areas without worrying about how time affects this system. The focus is solely on the spatial distribution of pressure and how it correlates to the fluid's weight above.
Examples & Analogies
Think of a beaker filled with different colored layers of fluids. Each layer creates pressure at the bottom due to its weight, and we can easily measure how this pressure changes from the top layer to the bottom without considering any time factors.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: Study of fluids at rest and their pressures.
-
Pascal's Law: Pressure applied in static fluids is transmitted uniformly.
-
Pressure Distribution: Understanding how pressure varies in fluids at rest.
-
Taylor Series Approximation: A method to simplify calculations for pressure fields.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Designing a dam involves calculating the pressure exerted by water at different heights to ensure structural integrity.
-
Analyzing how fluid pressure impacts the walls of a tank under static conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In hydrostatics we trust, nothing moves, that's a must!
📖 Fascinating Stories
-
Imagine a still pond; when you drop a stone, the ripples spread uniformly out—a perfect representation of Pascal's Law!
🧠 Other Memory Gems
-
Remember P-V-T, Pressure, Velocity, Temperature; but at rest, V and T are still and we only measure P!
🎯 Super Acronyms
Remember **H-A-C**
- Hydrostatics
- Applications of pressure
- and Capillarity!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces and pressures associated with them.
-
Term: Pressure
Definition:
The force exerted per unit area exerted by a fluid at rest.
-
Term: Pascal's Law
Definition:
A principle stating that pressure applied in a confined fluid is transmitted equally in all directions.
-
Term: Taylor Series
Definition:
A mathematical series used to approximate functions by summing their derivatives at a single point.