Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Welcome, everyone! Today, we're diving into hydrostatics, which deals with fluid behavior when it's at rest. Can someone tell me what you think happens to pressure in a liquid that's not moving?
I think the pressure would stay constant if the fluid is undisturbed.
Exactly! Pressure is constant throughout the fluid at rest. This brings us to Pascal's Law, which states that the pressure applied to a confined fluid is transmitted unchanged in all directions. Can anyone remember what this means practically?
It means if you apply pressure to one part of a fluid in a closed container, other parts feel that pressure too!
Great point! Let’s remember it with the acronym P for Pascal, P for Pressure: 'Pascal-Protects Pressure'.
Pressure Forces in Hydrostatics
Unlock Audio Lesson
Next, let's examine how pressure forces act on fluid elements. What forces do you think are at play in a fluid at rest?
I guess gravity would be one of them?
Correct! The main forces are gravity and pressure. In static conditions, gravity pulls the fluid down while pressure from below pushes it up. When these forces balance, we can derive certain relationships. Can anyone see the relationship between pressure and depth in a fluid?
Isn’t it true that pressure increases with depth?
Exactly! The deeper you go, the greater the pressure due to the weight of the liquid above. Remember, for every 1 meter depth, the pressure increases by about 9.81 kPa - a key concept in hydrostatics.
Hydrostatic Pressure Distribution
Unlock Audio Lesson
Now let's discuss hydrostatic pressure distribution. Can anyone tell me what it means for a fluid in a container?
I think it describes how pressure varies with depth.
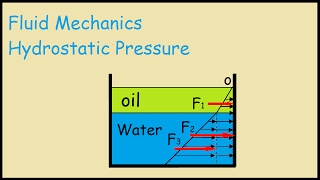
Right! The variation is linear. For example, the pressure at a depth h can be calculated using the formula P = ρgh, where ρ is the fluid density, g is acceleration due to gravity, and h is the depth. What applications can you think of that use this principle?
I know barometers! They measure atmospheric pressure based on fluid heights.
Capillary action in plants also uses hydrostatic pressure, right?
Absolutely! Let's keep these connections in mind for real-world applications.
Applications of Hydrostatics
Unlock Audio Lesson
Today, we want to see how these concepts apply in real life. Consider a dam; what do you think happens to the pressure exerted on the dam wall?
The pressure would increase as we go deeper from the top of the water to the bottom.
Exactly! As the water pressure increases with depth, engineers must take that into account when designing the dam to withstand these pressures. So, who remembers the formula we discussed for calculating this pressure?
P = ρgh, right?
Yes, and in tanks or oil reservoirs, we must assess the same principles! Applying what we've learned helps engineers ensure the safety and efficiency of these systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore hydrostatics, emphasizing fluid behavior at rest. Key topics include Pascal's law, pressure forces on fluid elements, concepts of gauge pressure, vapor pressure, and hydrostatic pressure distributions, as well as real-world applications like barometers and capillary effects.
Detailed
Hydrostatics
In the study of fluid mechanics, hydrostatics refers to the behavior of fluids at rest. This section outlines the fundamental principles governing fluid statics, including Pascal's Law, which states that pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid. The section begins with a review of prior concepts, emphasizing the significance of pressure fields in static fluids. There is a focus on various types of pressure, such as gauge pressure and vapor pressure, and how they affect hydrostatic pressure distribution. Applications of these concepts are illustrated through examples such as barometers and capillary action. The concluding emphasis is on understanding how pressure is exerted by a stationary fluid, integral to multiple engineering disciplines.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now. Like as I said it any fluid flow problems we look at either the pressure field, the velocity field, or the density and temperature field. When the fluid is rest now, very simply way the velocity vectors becomes zero and if I consider incomprehensible the density is a constant and if the temperature is not very much I need not need a thermodynamics first laws to define the problems. Then only the left is that the pressure field. That means when fluid is at rest conditions only we need to know it how the pressure variations is going over these fluid domains. That is what the simplified problems.
Detailed Explanation
When we talk about a 'fluid at rest', it means that there are no movements in the fluid. This causes the velocity to be zero, meaning there’s no flow. For incompressible fluids, like most liquids, the density remains constant. In this state, the only factor we need to study is the pressure in the fluid, which can vary depending on where you measure it. The rest simplifies our calculations since we don't have to worry about changes in velocity or temperature, allowing us to focus solely on how pressure works within the fluid.
Examples & Analogies
Think of a calm lake on a still day. The water is not moving (it's at rest), which means the pressure at different depths just depends on how deep you go. If you were to dive into the lake, the deeper you go, the more pressure you feel – and that’s because the weight of the water above you is pushing down.
Gravity and Pressure Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress. So when a fluid is at rest, there is no shear stress acting on that. So you can take a surface or take a control volume. Over that control surface you can define it the shear stress components become zero. That is very simplified now that any control volume you consider it over that control volume surface as the fluid is at rest conditions, there is no shear stress acting on the control surface. So that is the very easy problems what we have now. And what the two forces we have? The gravity force and the force due to the pressure distribution.
Detailed Explanation
In a fluid at rest, since there’s no flow, there’s no change in velocity – this means there are no shear stress forces acting on the fluid. Shear stress is the resistance to flow, and it occurs when layers of fluid are in motion relative to each other. Therefore, we can simplify our analysis by focusing on two forces: gravity, which pulls the fluid downwards, and the pressure of the fluid acting outward. This makes it much easier to understand how pressures behave in a stationary fluid.
Examples & Analogies
Think of a swimming pool that’s not being disturbed by waves or people. The water isn’t moving; the only forces at play are the weight of the water (gravity) and the pressure it exerts on the walls and bottom of the pool. Imagine holding a ping pong ball under the water - the pressure will be greater at greater depths because of the weight of the water above it, but the ball remains still as long as there are no external disturbances.
Applying Hydrostatic Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So whatever the pressure distribution forces that what is equate with the gravity force. Very simple things now, and since is a fluid is at the rest, so you can say that there is no mass flux is coming into the any control volumes or the momentum flux or no external work done it. So this is the what the simplified case. Like for example, if you take this dam, which is 100-meter-high and we have a reservoir, let you consider this is what 90 meter height from the bottom. That is what the water levels is 90 meter from the bottom.
Detailed Explanation
In simple terms, we can balance the forces in a fluid at rest by equating the pressure forces to the gravitational forces. For example, consider a dam. The height of the water behind a dam (90 meters in this case) creates pressure that acts on the dam walls. We can calculate how much pressure is acting at different depths based on the weight of the water above. Since the fluid is at rest, we also know that no additional forces (like movement of the water or external work) are acting against this balance.
Examples & Analogies
Imagine a tall glass of water sitting on a table. The water is at rest, and the pressure at the bottom of the glass increases as more water is added. You can feel this increase if you tap your finger against the bottom of the glass. Just like that glass of water, the pressure due to the depth of water applies the same way behind a dam, ensuring we can design it to withstand that pressure without collapsing.
Pascal's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now whenever I am talking about that I am looking for a pressure field as the fluid is at rest. So basically I am looking at the pressure is a function of the positions. Time is not there, as the fluid is at rest condition. The many of the times when you consider the pressure field, you try to look it from one point to other point. ... So fluid flow what we are considering here all the cases the pressure is a scalar quantity and that what they must stated by Pascal’s law.
Detailed Explanation
Pascal's law states that when a fluid is at rest, the pressure exerted on an enclosed fluid is transmitted equally in all directions. This means that if you push on one part of a contained fluid, that pressure is felt throughout the fluid uniformly. Mathematically, you can represent changes in pressure at different locations using functions indicating positions in space. Essentially, it confirms that pressure does not depend on the direction of application; it acts as a scalar quantity.
Examples & Analogies
Imagine filling a balloon with air. If you squeeze one side, you can feel the pressure on the opposite side increase even though you didn’t touch that area at all. This is because the air compresses and thus transmits that pressure throughout the entire balloon. Similarly, in a fluid at rest, any pressure applied at one point is felt everywhere.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: Refers to the study of fluids at rest, essential for understanding fluid behavior in design and transport.
-
Pascal's Law: A fundamental principle that describes fluid pressure transmission in a closed system.
-
Pressure Distribution: The concept that fluid creates varying pressure based on depth, relevant in engineering.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The pressure increase in a dam due to the height of water above it, requiring careful engineering design.
-
The rise of liquid in a straw due to capillary action, demonstrating hydrostatic principles in everyday life.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When counting on pressure that doesn’t stray, just remember it stays the same way.
📖 Fascinating Stories
-
Imagine a sealed jar filled with water. When you push down on one spot, all the water responds, showcasing Pascal’s law in action – pressure spreads equally.
🧠 Other Memory Gems
-
Remember the acronym 'P – Pressure, A – Applied, S – Steady', to recollect that pressure remains steady under Pascal's Law.
🎯 Super Acronyms
Use the acronym 'PDEP' - Pressure, Depth, Equal, Pascal to memorize the key concepts around hydrostatics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces and pressures associated with them.
-
Term: Pascal's Law
Definition:
The principle stating that pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid.
-
Term: Gauge Pressure
Definition:
The pressure relative to atmospheric pressure, commonly used in measuring pressure in fluids.
-
Term: Vapor Pressure
Definition:
The pressure exerted by a vapor in equilibrium with its liquid at a given temperature.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a liquid at rest due to the weight of the fluid above.
-
Term: Control Volume
Definition:
A defined region in space through which fluid may flow, used for analyzing fluid flows.