Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Welcome, class! Today we will dive into hydrostatics, focusing on fluids at rest. Can anyone explain what hydrostatics means?
It's the study of fluids that are not moving, right?
Exactly! Hydrostatics deals with how pressures change within a fluid that isn't flowing. Why do you think this concept is important?
Because we need to know how pressure acts in tanks and pipes!
Correct! Understanding pressure distributions helps in designing safe structures. A quick memory aid: remember BHPP - 'Before Hydrostatics, Pressure Prevails.' This reminds us that pressure calculations are vital early in design.
That makes sense! Can pressures differ across a fluid?
Yes! But how does pressure vary with depth? Let's explore that.
Understanding Pascal’s Law
Unlock Audio Lesson
Now, let's explore Pascal's Law. Who can tell me what this law articulates?
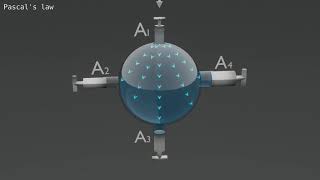
It says that pressure applied to an enclosed fluid is transmitted equally throughout the fluid.
Great job! Why do you think this principle is crucial in hydraulic applications?
Because it allows us to lift heavy loads easily with small forces!
Exactly! Pascal's Law is fundamental in hydraulics. To remember this, think of the acronym PHF - 'Pressure Helps Fluid!' Can anyone provide examples of where we see this in action?
Hydraulic brakes!
Yes! Hydraulic systems in vehicles are a perfect application. Remember, pressure in a fluid has no directional bias when it's at rest.
Pressure Distribution in Fluids
Unlock Audio Lesson
Let's talk about how pressure is distributed within a static fluid. What influences the pressure at a given point?
Depth! The deeper you go, the higher the pressure.
That's right! We can calculate this using the formula P = P0 + ρgz, where z is the depth. A good mnemonic is 'P-Pragmatically Equals P+ρgz.'
What's the significance of this in real-world applications?
These calculations are crucial in designing structures like dams, where we need to understand the pressure exerted on walls. When designing, we trust that pressure will be uniformly distributed across surfaces.
So, if the pressure is uniform, we can safely calculate the forces acting on structures?
Exactly! Very well summarized. Each aspect today builds on the previous concepts—hydrostatics, Pascal's Law, and pressure distribution.
Practical Applications of Pascal's Law
Unlock Audio Lesson
Let’s apply our knowledge of Pascal's Law. Where are some everyday examples we might find fluid at rest?
In tanks and reservoirs!
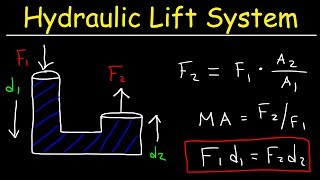
Good! Also consider hydraulic lifts used in car services. These systems rely on Pascal's Law. By applying a small force, a larger load can be lifted due to pressure transmission.
So, the smaller force creates enough pressure to lift heavier weights?
Correct! And remember, as we learnt earlier in the session, usage of structures relies on understanding these principles. So we can summarize—design effectively by respecting fluid mechanics laws.
Do we also see this in any other areas?
Absolutely! Pascal's Law is also seen in various medical devices such as syringes. They utilize fluid principles just like hydraulic systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
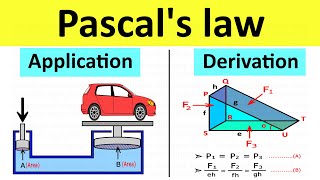
The section on Pascal’s Law discusses fluid mechanics at rest, emphasizing the significance of pressure in static fluids. Key topics include hydrostatics, the relationship between pressure and forces in fluid elements, and the scalar nature of pressure as described by Pascal's Law.
Detailed
Pascal’s Law
Pascal's Law, a fundamental principle in fluid mechanics, states that any change in pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid in all directions. In the context of hydrostatics, which deals with fluids at rest, understanding this law is essential for both theoretical and practical applications.
Key Concepts Covered
- Hydrostatics: The study of fluids at rest. In static conditions, features such as pressure variation become crucial as velocity and density gradients are negligible.
- Pressure in Fluids: When considering a fluid at rest, the pressure at any point within the fluid depends on the depth and density of the fluid. The pressure forces acting on any control volume are balanced against gravitational forces.
- Dynamics of Pressures: Pascal's Law can be mathematically expressed by considering forces in control volumes where pressure acts perpendicularly to surfaces. The balance of forces leads to relationships that show pressure remains constant in all directions within the fluid.
- Gravity Effects: In scenarios where the fluid is influenced by gravity, the pressure increases with depth due to the weight of the overlying fluid. This is critical in applications like dams and tanks where pressure calculations inform design and safety.
- Applications: Pascal's Law applies to various practical situations such as hydraulic systems and can be observed in devices like hydraulic lifts and brakes.
Understanding Pascal's Law helps in designing fluid systems and structures, ensuring they withstand internal pressures safely.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Pascal's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let come it to very basic law is called Pascal. As you when you fluid is rest let us consider is that the there will be a normal stress acting on any plane. Okay, that is what we are considering is that that what is the fluid pressure. Here I am considering a fluid element or you can say it the fluid control volume element or fluid control volume.
Detailed Explanation
Pascal's Law states that in a fluid at rest, any change in pressure applied to the fluid is transmitted undiminished throughout the fluid. This means that if the fluid is at rest and we apply pressure to it, that pressure affects every part of the fluid evenly. For example, if you push down on a closed container filled with water, that pressure is felt equally at every point within the container. The concept also implies that the pressure at any point within a fluid is transmitted in all directions equally, leading to a concept of normal stress acting on any plane in the fluid.
Examples & Analogies
Think of a balloon filled with water. If you squeeze the balloon at one point, you will notice that the water inside does not just compress at that location. Instead, the pressure you applied is felt throughout the entire balloon. This is a direct application of Pascal's Law.
Forces Acting on a Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
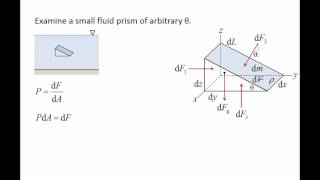
Now if you consider this is what my control volumes and along this perpendicular to this surface that is what my unit value. That means one unit I have considered perpendicular. This is a three dimensional control volume I am representing as a two dimensional thing. And I am defining the pressure P is acting on the surface, the P is x j acting on this surface and P is the pressure components acting on this inclined surface.
Detailed Explanation
In this context, a control volume is defined as a specified region in space through which we can analyze the behavior of the fluid. When we denote the force acting on a surface of this control volume, it's governed by the pressure at that surface. For instance, if there's a fluid at rest inside a container, the pressure on any surface of the control volume can be calculated based on the pressure acting perpendicular to that surface. Therefore, the equilibrium conditions (sum of forces acting = 0) apply for the control volume analysis.
Examples & Analogies
Imagine a cube submerged in water. Each face of the cube experiences pressure from the water acting on it. The amount of force acting on each of these faces helps in understanding how the cube will behave when forces are applied, such as if it will float or sink.
Equilibrium Conditions in a Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if it is that when the fluid is rest we can find out some of the forces acting on this control volume should equal to zero. So then we can look it force in a scalar component in x direction and the y direction. That means the force component in x direction should be equal to zero. Force component in the z direction should equal to zero.
Detailed Explanation
In a fluid at rest, the forces acting on a control volume should be balanced, meaning they sum to zero. Specifically, this means that the downward forces (like gravity) and the upward forces (like pressure) must be equal. For instance, if we look at a small element of fluid, we can write the equations for the forces in the x, y, and z directions. By setting these equal to zero, we can analyze the fluid's conditions, contributing to our understanding of pressure distribution.
Examples & Analogies
Consider a swimming pool. The water at rest provides equal pressure on the bottom of the pool as well as on the walls. If you put a weight at the bottom, for instance, the amount of water pushing up is exactly equal to the weight of the object, maintaining equilibrium in that fluid.
Calculating Pressure in Different Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
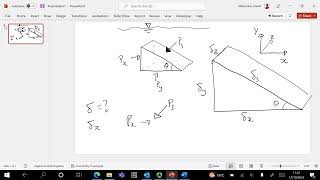
As the fluid is at rest, summation of forces in x and z directions must be equal to zero. ∑F_x = 0 = P_b Δz - P_b Δs sin(θ).
Detailed Explanation
To calculate the pressure acting in different directions within a fluid at rest, we can formulate equations that balance the forces in the x and z directions. This relationship helps in calculating how pressure varies with depth in any fluid. Each pressure component is multiplied by the area they act upon, creating an equilibrium where upward pressures balance the forces acting downward (like weight). The equilibrium equations yield the relationships needed to understand how pressure across various surfaces is distributed as a result of gravity and fluid properties.
Examples & Analogies
Think of a high-rise building filled with water in tanks on each floor. The pressure at the base of these tanks is different from that at the top due to the weight of the water above them. Thus, the water pressure at the bottom (deepest point) is calculated based on the water column above it, demonstrating the principles described in this chunk.
Conclusion of Pascal's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But in case when you have a rigid body motion, the fluids work as a rigid body motions like the tank is going moving with a constant acceleration of a, the similar conditions can be considered it any liquid field containers moving with the constant accelerations a.
Detailed Explanation
When a fluid is not just sitting still but in motion, under constant acceleration, it still follows the principles outlined by Pascal's Law. In these scenarios, while the fluid itself may not exhibit typical fluid behavior, it maintains a pressure distribution based on its internal forces and effects from external motions. The law still holds true that the pressure within the fluid has equal effects in all directions as if it were at rest, provided that there is no velocity gradient acting which would create shear stress.
Examples & Analogies
Imagine you're in a car that suddenly accelerates. The liquid in a cup on your dashboard leans back towards the seat due to the acceleration. While the liquid is still, its pressure distribution changes due to this external acceleration, illustrating that among accelerating fluids offer a dynamic description while adhering to principles strong in instrumental physics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: The study of fluids at rest. In static conditions, features such as pressure variation become crucial as velocity and density gradients are negligible.
-
Pressure in Fluids: When considering a fluid at rest, the pressure at any point within the fluid depends on the depth and density of the fluid. The pressure forces acting on any control volume are balanced against gravitational forces.
-
Dynamics of Pressures: Pascal's Law can be mathematically expressed by considering forces in control volumes where pressure acts perpendicularly to surfaces. The balance of forces leads to relationships that show pressure remains constant in all directions within the fluid.
-
Gravity Effects: In scenarios where the fluid is influenced by gravity, the pressure increases with depth due to the weight of the overlying fluid. This is critical in applications like dams and tanks where pressure calculations inform design and safety.
-
Applications: Pascal's Law applies to various practical situations such as hydraulic systems and can be observed in devices like hydraulic lifts and brakes.
-
Understanding Pascal's Law helps in designing fluid systems and structures, ensuring they withstand internal pressures safely.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a dam, water pressure increases with depth due to the weight of water above, affecting the design and integrity of the structure.
-
Hydraulic brakes in vehicles utilize Pascal's Law where pressing on the brake pedal creates pressure that operates brake pads on each wheel.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In water deep, the pressure creeps, from low to high, it never sleeps.
📖 Fascinating Stories
-
Imagine a scuba diver who finds that as they descend deeper into the ocean, the weight of water above them presses harder, demonstrating Pascal’s Law.
🧠 Other Memory Gems
-
P-E-D: Pressure Equals Depth, remember it means pressure increases as you go deeper.
🎯 Super Acronyms
B-PAR for 'Before Pressure Always Resides' - remember that pressure is consistent in a static fluid.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The branch of fluid mechanics that studies fluids at rest and the forces and pressures associated with them.
-
Term: Pascal’s Law
Definition:
A principle stating that changes in pressure applied to a confined fluid are transmitted undiminished to every portion of the fluid.
-
Term: Pressure
Definition:
The force exerted per unit area within fluids, typically measured in pascals (Pa).
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, used for analyzing fluid behavior.
-
Term: Gauge Pressure
Definition:
The pressure measured relative to atmospheric pressure, often used in practical scenarios.
-
Term: Hydraulic Systems
Definition:
Systems that use pressurized fluid to perform work, such as in lifts and braking systems.
-
Term: Equilibrium Conditions
Definition:
Situations where forces acting within a system balance each other, resulting in no net movement.