Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Today, let's delve deeper into hydrostatics. Hydrostatics is the study of fluids at rest and their pressure behavior. Can anyone tell me what we mean by fluids being at rest?
I think it means there’s no motion in the fluid.
Exactly! When fluids are at rest, their velocity gradient is zero, and as a result, they exert pressure uniformly. This brings us to Pascal's Law. Who can explain what Pascal's Law states?
It states that pressure applied to a confined fluid is transmitted undiminished in all directions.
Very well! One way to remember this is to think of a balloon filled with water. If you squeeze it, the water pushes back in all directions evenly. It’s a practical application of Pascal’s Law.
Pressure Types and Concepts
Unlock Audio Lesson
Next, let's talk about different types of pressure we encounter in fluid mechanics: gauge pressure, vapor pressure, and hydrostatic pressure. Can anyone tell me what gauge pressure is?
Isn’t gauge pressure the pressure relative to atmospheric pressure?
Yes! You got it right. Now, what about vapor pressure? Student_4?
Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid at a certain temperature.
Great explanation! Remember these definitions as they will play a crucial role when dealing with hydrostatic pressure distributions.
Can you explain how we use hydrostatic principles in real life?
Sure! One common example is a barometer used to measure atmospheric pressure. It simply relies on the hydrostatic principle to gauge how heavy the air is above it.
Practical Applications of Hydrostatics
Unlock Audio Lesson
Now that we understand the principles of hydrostatics, let’s discuss specific applications. Why do you think understanding pressure distribution is essential in dam designs?
I guess because the pressure from the water must be calculated correctly to ensure the dam can withstand it.
Precisely! Engineers must consider the hydrostatic pressure at various depths to design safe structures. How about the capillary effect?
The capillary effect is when water rises in a narrow space due to adhesive forces.
Correct! The capillary effect is crucial in the design of various structures, including soil and plant systems. In summary, understanding hydrostatics not only helps us in theoretical problems but is vital in numerous practical applications.
Summary and Application of Taylor Series
Unlock Audio Lesson
To summarize what we've learned, fluid properties such as pressure can be expressed as functions. We use Taylor series for approximating these functions. What does that mean for practical problems?
It means we can estimate pressures or velocities at different points in a flow field.
Exactly! In most fluid problems, we don’t use the higher order terms because they tend to be negligible.
How do you decide which terms to keep?
We usually keep terms that have a significant impact, commonly the first and second derivatives. This simplifies our calculations while maintaining accuracy.
Got it! It all ties back in to our earlier discussions on pressure fields and forces in a fluid system.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section captures essential points from the prior lectures, including the concept of hydrostatics, Pascal's law, and the role of pressure in fluid mechanics, especially when fluids are at rest. It sets the stage for more complex fluid dynamics discussions.
Detailed
Summary of Previous Lectures
This section provides a comprehensive recap of the key concepts discussed in previous fluid mechanics lectures, particularly focusing on hydrostatics—essentially the study of fluids at rest. The lecture references important textbooks, such as those by Cengel & Cimbala and F.M. White, for additional study.
Key points include:
- Hydrostatics: The primary focus of the current lecture. Hydrostatics examines how fluids exert pressure when they are not in motion.
- Pressure Calculations: Understand the pressure force acting on a fluid element, utilizing control volumes for analysis.
- Types of Pressure: Definitions of gauge pressure and vapor pressure, along with hydrostatic pressure distributions, are discussed.
- Practical Applications: Real-world implications, such as the workings of barometers and capillary action, are highlighted to reiterate the importance of hydrostatics in engineering contexts.
- Foundational Concepts: Descriptions of velocity fields, pressure fields, and the methods employed for their analysis—experimental, computational, and analytical approaches.
- Pascal’s Law: Introduction to how fluids exert equal pressure in all directions when at rest, leading to the understanding that pressure is a scalar quantity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Recap of Fluid Mechanics Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
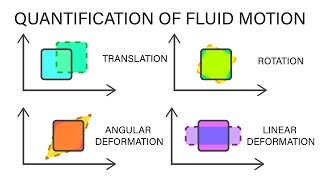
Now let us recap it, as of now what we learnt it. We already know it we talk about a either a system approach or the control volume approach to solve the fluid mechanics problems. And whenever you solve the fluid mechanics problems as I said it in the last class, we generally look for three velocities three fields, velocity field, pressure field and the density field. But when fluid is incompressible, then we just look for the pressure field and the velocity field. So these two fields we can get it using this three different approaches as I discussed earlier. One is experimental method, conducting the experiment in a wind tunnel, computational approach, which is a computational fluid dynamic now extensively used for very complex fluid flow problems or this analytical approach with a very simplified problem we can solve analytically to get the gross approximations of this pressure field the and the velocity field.
Detailed Explanation
In this chunk, the professor recaps what has been learned in previous lectures about fluid mechanics. It emphasizes the difference between the system approach and the control volume approach for solving fluid mechanics problems. There are three main fields to consider: velocity, pressure, and density. When dealing with incompressible fluids, only the pressure and velocity fields are considered. The professor then identifies three main methods for analyzing these fields: 1) Experimental methods, where measurements are taken directly from physical experiments (like wind tunnels), 2) Computational methods that simulate fluid dynamics through complex algorithms, and 3) Analytical methods that involve solving equations for simpler problems, allowing for approximations of the velocity and pressure fields.
Examples & Analogies
Consider a car's design process. Engineers might conduct experiments in wind tunnels (experimental method) to see how air flows around the vehicle. They can also use computer simulations (computational method) to predict fluid behavior under different conditions, and finally use mathematical formulas (analytical method) to simplify the analysis of forces acting on the car's body.
Understanding Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now. Like as I said it any fluid flow problems we look at either the pressure field, the velocity field, or the density and temperature field. When the fluid is rest now, very simply way the velocity vectors becomes zero and if I consider incomprehensible the density is a constant and if the temperature is not very much I need not need a thermodynamics first laws to define the problems. Then only the left is that the pressure field.
Detailed Explanation
This section introduces the concept of fluid at rest, which is a fundamental idea in fluid mechanics. When a fluid is at rest, it means there is no movement, and this greatly simplifies the analysis. The velocity vectors of the fluid are zero, and for incompressible fluids, the density remains constant. This means that factors like temperature can often be neglected for simplification. Therefore, the focus is shifted only to the pressure field, which is crucial in understanding how pressures vary throughout the static fluid body.
Examples & Analogies
Imagine a glass of water sitting on a table. Since the water is not moving, there are no currents or waves; the velocity is zero. In this state, the pressure at any point in the water depends solely on the weight of the water above that point and is equal across all directions, which makes it easier to compute how the water exerts force on the bottom of the glass.
Gravity and Pressure Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress. So when a fluid is at rest, there is no shear stress acting on that. So you can take a surface or take a control volume. Over that control surface you can define it the shear stress components become zero. That is very simplified now that any control volume you consider it over that control volume surface as the fluid is at rest conditions, there is no shear stress acting on the control surface.
Detailed Explanation
When analyzing a fluid at rest, another critical aspect is the absence of shear stress. Shear stress occurs when there are velocity gradients, but in stationary fluids, these gradients don't exist. Therefore, if we analyze any surface within the fluid, the shear stress acting on that surface is zero. The forces we then analyze can be simplified to only look at gravity and pressure forces acting on the fluid. This fundamental idea allows us to make easier calculations regarding the behavior of the fluid without worrying about additional complexities of shear.
Examples & Analogies
Think of a swimming pool filled with water. When no one is swimming, the water is still, and thus, the pressure on the bottom of the pool results solely from the weight of the water above it (gravity). Because the water is not moving, you don’t have to worry about currents or waves, making it easier to calculate the pressure at any point.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: Study of fluids at rest.
-
Pressure: Force per unit area exerted by a fluid.
-
Pascal's Law: Pressure is transmitted equally in all directions in a fluid at rest.
-
Gauge Pressure: Pressure relative to atmospheric pressure.
-
Vapor Pressure: Pressure exerted by vapor above a liquid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A barometer measuring atmospheric pressure using hydrostatic principles.
-
Pressure distribution across the surface of a dam due to water at rest.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Hydrostatics is calm and still, pressure works like a powerful thrill.
📖 Fascinating Stories
-
Imagine a balloon filled with water. When you squeeze it, water pushes equally out in every direction, illustrating Pascal's Law perfectly.
🧠 Other Memory Gems
-
Remember 'H2O' for Hydrostatics, 'P' for Pascal's law, 'P' for Pressure, 'G' for Gauge Pressure and 'V' for Vapor Pressure.
🎯 Super Acronyms
H-P-G-V
- Hydrostatic - Pascal's law - Gauge pressure - Vapor pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces and pressures they exert.
-
Term: Pascal's Law
Definition:
A principle stating that pressure applied to a confined fluid is transmitted undiminished in all directions.
-
Term: Gauge Pressure
Definition:
Pressure relative to atmospheric pressure.
-
Term: Vapor Pressure
Definition:
The pressure exerted by a vapor in equilibrium with its liquid at a given temperature.
-
Term: Hydrostatic Pressure Distribution
Definition:
The variation of pressure in a fluid at rest, typically increasing with depth.