Mathematical Formulation of Pascal’s Law
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we're discussing hydrostatics, which focuses on fluids that are at rest. What do you think happens to the pressure in a fluid at rest?

Isn't the pressure uniform throughout the fluid?

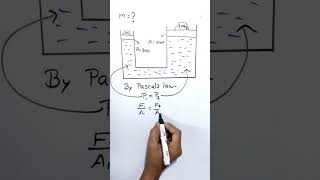
Exactly! This leads us to Pascal's Law. Can anyone explain what Pascal's Law states?

It says that a change in pressure at any point in a confined fluid is transmitted equally in all directions.

Great! This is fundamental in applications such as hydraulic systems. Let's remember this with the acronym P.E.T. — Pressure Equally Transmitted.
Pressure in a Fluid at Rest
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When a fluid is at rest, how do we determine the pressure at different depths?

The pressure increases with depth due to the weight of the fluid above.

Correct! Pressure can be calculated using the equation P = ρgh, where ρ is the fluid density and h is the height. What does this signify in practical terms?

It means that deeper in a tank or well, the pressure will be higher.

Exactly! We often use this in designing tanks and dams.
Mathematical Approach - Taylor’s Series
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss how we can use Taylor's series to approximate changes in pressure. Who can provide a summary of this series?

It lets us express a function as a series of terms calculated from the function's derivatives.

Yes! And when approximating in fluid mechanics, we often ignore higher order terms as they become negligible. Can anyone give me an example?

If we know the pressure at one depth, we can estimate it at another nearby depth using the first derivative.

Great job! This technique is valuable when dealing with slight changes in pressure within fluid systems.
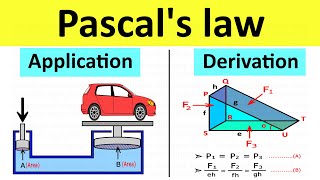
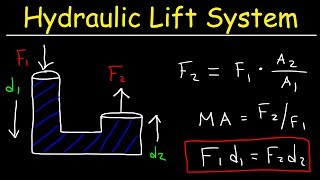
Pascal's Law Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's explore the practical applications of Pascal's Law. What comes to mind?

Hydraulic lifts and brakes!

Indeed! Can anyone explain how a hydraulic lift works?

Pressure applied to one piston creates equal pressure in a larger piston, lifting heavy loads.

Spot on! This basic principle is at the heart of many powerful machines.
Summary of Pascal’s Law
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

To conclude, what are the main points we've covered about Pascal's Law?

It describes how pressure in a fluid at rest transmits equally in all directions.

And the pressure increases with depth due to the gravitational force!

Fantastic! Remember these key ideas as they are fundamental in both fluid mechanics and numerous engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section discusses how fluids at rest do not exhibit velocity gradients and how pressure variations can be mathematically formulated using Pascal's Law. It emphasizes the equilibrium forces acting on fluid elements, illustrated by examples such as dams and accelerating tanks.
Detailed
Mathematical Formulation of Pascal’s Law
In this section, we delve into the principles of fluid mechanics focusing on fluids at rest, termed hydrostatics. At equilibrium, static fluids exhibit pressure distributions influenced by weight and external forces. Pascal's Law states that any change in pressure applied to a confined fluid is transmitted undiminished throughout the fluid. Specifically, we analyze how pressure varies with depth, highlighted through examples such as dams and tanks.
Key ideas include:
- The concept that liquid under rest has no shear stress due to absence of velocity gradients.
- Mathematical relationships expressed via Taylor series to approximate pressure variations within static fluids.
- Understanding of gauge, vapor, and hydrostatic pressures, linking to real-world applications such as barometers and tank design.
Ultimately, this segment not only formulates the mathematical expressions governing fluid static conditions but also lays down the foundational knowledge for more complex fluid dynamics.
Youtube Videos
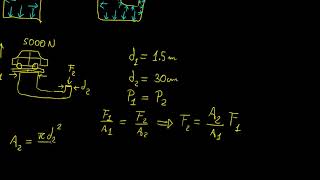




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Pascal’s Law
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now let come it to very basic law is called Pascal. As you when you fluid is rest let us consider is that the there will be a normal stress acting on any plane.
Detailed Explanation
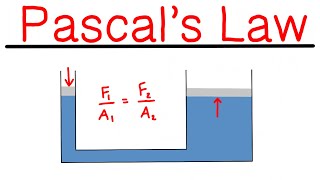
Pascal's Law states that in a fluid at rest, the pressure exerted on any part of the fluid is transmitted undiminished throughout the fluid. This means that any change in pressure applied at any point in a confined fluid will be felt equally throughout the fluid. This normal stress acting on any plane is crucial to understanding how fluids behave under pressure.
Examples & Analogies
Consider a fully sealed balloon. When you press down on one part of the balloon, the pressure is felt throughout the entire balloon, causing it to change shape. This is a practical demonstration of Pascal's Law as the pressure is transmitted equally in all directions.
Equilibrium of Forces in a Fluid Element
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Here I am considering a fluid element or you can say it the fluid control volume element or fluid control volume. Now if you consider this is what my control volumes and along this perpendicular to this surface that is what my unit value.
Detailed Explanation
When analyzing a fluid element at rest, we assume it is in equilibrium, meaning all the forces acting on it must balance out. The pressure acting on different surfaces will produce forces that must be equal to maintain this equilibrium. Therefore, the sum of the forces in any direction (x or z) must be zero. This leads to an understanding of how pressure varies within the fluid element.
Examples & Analogies
Think of a car tire filled with air. The air pressure inside the tire pushes against the walls of the tire evenly, ensuring that it maintains its shape. If the pressure is not balanced, the tire could either deflate or burst, illustrating the importance of equilibrium of forces in fluids.
Mathematical Formulation of Equilibrium Conditions
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
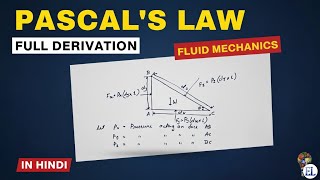
As the fluid is at rest, summation of forces in x and z directions must be equal to zero. ∑F_x = 0 = P_b Δz - P_b Δs sin θ; ∑F_z = 0 = P_b Δx - P_b Δs cos θ - ρgΔx Δz.
Detailed Explanation
To derive the pressure relationships in a fluid at rest, consider the forces in both the x and z directions. These equations represent the balance of pressure forces acting on the surfaces of the fluid element and the weight of the fluid. This understanding leads to the formulation that allows us to relate the pressure at different points within the fluid. As Δs becomes infinitesimally small, we visualize the condition of uniform pressure in all directions.
Examples & Analogies
Imagine a column of water in a tall glass. The pressure at the bottom of the glass is equal to the weight of the water above it and reflects the influence of gravity. If you were to take very small sections of the glass and apply the principles mentioned, you'd find that the pressure is consistently calculated based on the weight of the water, defending the equilibrium conditions.
Implications of Pascal’s Law
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
That is what is the Pascal law. And since pressure is same in all the directions, so we can consider is a pressure is a scalar quantity and that what they must stated by Pascal’s law.
Detailed Explanation
Pascal's Law indicates that pressure in a fluid at rest is isotropic—meaning it is the same in all directions. This leads us to treat pressure as a scalar quantity rather than a vector, simplifying calculations in fluid mechanics significantly. This scalar nature of pressure is fundamental for calculations involving forces, stress, and fluid dynamics.
Examples & Analogies
A simple way to think about this is with a soccer ball. If you apply pressure on one point of the ball, the air pressure inside the ball works equally in all directions, keeping the ball firm. This illustrates how pressure acts uniformly in every direction within a fluid, enabling us to apply Pascal's principle effectively in engineering and real-world applications.
Key Concepts
-
Hydrostatics: Study of fluids at rest.
-
Pascal's Law: Pressure changes are transmitted equally in fluids.
-
Pressure-Depth Relationship: Pressure increases with depth in a fluid.
-
Equilibrium Forces: Forces must balance in a system at rest.
Examples & Applications
In a swimming pool, as you dive deeper, the pressure on your ears increases due to the water above you.
Designing a dam requires understanding the pressure exerted by water at different depths to ensure structural integrity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a tank that's filled to the brim, pressure rises like a hymn. Depth increases, feeling the weight; pressure goes up, just contemplate.
Stories
Imagine a fish in the ocean swimming deeper and feeling its ears pop as pressure builds around. This journey explains Pascal's Law, where as depth increases, pressure isn't just a flaw.
Memory Tools
Remember 'P.E.T.' - Pressure Equally Transmitted, to recall Pascal's Law quickly.
Acronyms
H.O.P. - Hydrostatics, Observing Pressure increases as we go deeper.
Flash Cards
Glossary
- Hydrostatics
The study of fluids at rest and the conditions under which they remain in equilibrium.
- Pascal's Law
A principle stating that any change in pressure applied to a confined fluid is transmitted undiminished throughout the fluid.
- Pressure (P)
The force exerted per unit area within a fluid, typically measured in Pascals (Pa).
- Density (ρ)
A measure of mass per unit volume of a substance, influencing fluid pressure.
- Gauge Pressure
The pressure relative to atmospheric pressure, often used in fluid mechanics.
- Hydrostatic Pressure
The pressure exerted by a fluid in static equilibrium due to the force of gravity.
Reference links
Supplementary resources to enhance your learning experience.
