Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Welcome class! Today we delve into hydrostatics, which is the study of fluids at rest. Can anyone tell me what happens to the velocity of a fluid in this state?
I think the velocity is zero when the fluid is not moving.
Exactly! When a fluid is at rest, its velocity vector is zero, and therefore there are no shear stresses acting on it. This simplifies our analysis. To remember this, you can think of the acronym ‘REST’ – it stands for 'Resting Equals Static Tension.'
What about pressure? How does that change when the fluid is at rest?
Great question! The pressure in a fluid at rest varies with depth due to the weight of the fluid above it. This pressure distribution is fundamental in hydrostatics.
And how are these principles useful in real-world applications?
Hydrostatic principles are crucial for designing structures like dams and tanks. Understanding how pressure is distributed helps engineers assess the forces acting on these structures.
To summarize, fluid at rest has no velocity leading to no shear stresses, and pressure increases with depth due to the weight of the fluid.
Understanding Pascal’s Law
Unlock Audio Lesson
Building on our last discussion, let's delve deeper into Pascal's law. Can one of you explain what Pascal's law states?
I believe it says that pressure applied to an enclosed fluid is transmitted undiminished throughout the fluid.
Correct! This principle means that if you push down on one part of a fluid in a container, the pressure increases equally everywhere in that fluid.
Why is this important in engineering?
Understanding Pascal's law allows engineers to design hydraulic systems, which rely on this principle to lift heavy loads efficiently. Let's remember 'PUSH' — Pressure Used Superbly Helps! It encapsulates the utility of Pascal’s law.
Can you give an example where this is applied?
An everyday example is a hydraulic lift in garages, where small input forces can lift heavy vehicles, thanks to the principles established by Pascal's law.
Today we learned that Pascal's law is fundamental because of its role in hydraulic systems and its impact on fluid mechanics.
Pressure Distribution in Fluids
Unlock Audio Lesson
Now that we've discussed pressure and Pascal's law, let’s look at how pressure distributes itself in fluids at rest. What influences pressure at a certain depth?
I think it's the height of the fluid above that point, right?
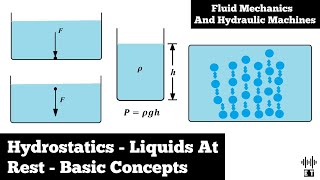
Exactly! The pressure at a depth is calculated by the equation P = ρgh, where ‘h’ is the height of the fluid column above the point. Remember 'DIVE': Depth Influences Vital Energy, which is a mnemonic for pressure dependence on depth.
And what about gauge pressure?
Gauge pressure is the pressure relative to atmospheric pressure. It doesn't include the atmospheric component. Always remember that gauge pressure is important when measuring forces in systems exposed to the environment.
What about real-life scenarios, Teacher?
One common application is measuring fluid pressure in a tank. For instance, understanding whether a tank can withstand the pressure exerted by the liquid inside is vital for safety.
In summary, pressure varies with depth and is influenced by the height of the fluid column above. Understanding gauge pressure is crucial in practical applications.
Applications of Hydrostatics
Unlock Audio Lesson
Finally, let's look at practical applications of hydrostatics such as barometers and the capillary effect. Who can tell me what a barometer does?
A barometer measures atmospheric pressure!
Correct! It utilizes a column of mercury, where the height of the mercury reflects atmospheric pressure. Think of 'PRESS' — Pressure Realized Effectively States Statics; it's a way to remember how we gauge atmospheric pressure.
What about the capillary effect?
The capillary effect occurs when liquid rises in a narrow tube. This phenomenon is due to the adhesive forces between the liquid and the tube's surface surpassing cohesive forces within the liquid.
Why is understanding this effect important?
It's essential in various fields, such as agriculture and biology—think of how plants absorb water through capillary action.
To summarize, we explored crucial applications of hydrostatics in barometers and the capillary effect, emphasizing their importance in real-world scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Hydrostatics deals with fluids that are not in motion. Key topics in this section include the concept of pressure at rest, Pascal's law, pressure variations in fluids, and practical applications like barometers and capillary effects.
Detailed
This section, titled 'Concepts of Hydrostatic', provides a comprehensive overview of fluid statics, emphasizing the behavior of fluids at rest. The lecture begins with a recap of previous topics, leading into the foundational concept of hydrostatics where the velocity vector equals zero under static conditions. Key principles include Pascal's law, which states that pressure in a fluid is transmitted equally in all directions, and the various types of pressures such as gauge pressure and vapor pressure. The discussion explores hydrostatic pressure distributions and applies these concepts to practical scenarios, such as the calculation of pressures exerted on dam surfaces and the behavior of fluids in an accelerating tank, demonstrating the fluid's action akin to a rigid body motion. The chapter concludes with an emphasis on the significance of understanding these foundational concepts in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now. Like as I said it any fluid flow problems we look at either the pressure field, the velocity field, or the density and temperature field. When the fluid is rest now, very simply way the velocity vectors becomes zero and if I consider incomprehensible the density is a constant and if the temperature is not very much I need not need a thermodynamics first laws to define the problems. Then only the left is that the pressure field.
Detailed Explanation
When we talk about fluid at rest, we refer to a state where the fluid does not exhibit any movement. In this scenario, the velocity of the fluid is zero. No flows or disturbances occur, meaning that there are no variations in velocity or shear stress acting on the fluid. Consequently, we only need to consider pressure variations within the fluid, because in the absence of fluid motion, density remains constant and temperature effects are negligible, simplifying our analysis to just the pressure field.
Examples & Analogies
Imagine a glass of water sitting on a table. The water is perfectly still, with no waves or movement. In this case, we only need to think about the pressure the water exerts against the bottom of the glass due to gravity, and we don't have to consider any other factors, like the velocity of the water, because there's none to measure.
Forces in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress. So when a fluid is at rest, there is no shear stress acting on that. So you can take a surface or take a control volume. Over that control surface you can define it the shear stress components become zero. That is very simplified now that any control volume you consider it over that control volume surface as the fluid is at rest conditions, there is no shear stress acting on the control surface.
Detailed Explanation
In a fluid at rest, shear stress is non-existent due to the lack of velocity gradients. Essentially, shear stress arises because of the movement of one layer of fluid over another. With no movement occurring, there are no gradients to create this force. This simplification means we can analyze forces acting on a given control volume without having to account for any shear stresses, making it easier to determine the overall behavior of the fluid's pressure forces.
Examples & Analogies
Think of a thick layer of honey sitting still in a jar. If you were to look at two layers of honey, one on top of the other, they would not slide past each other because the honey is at rest. In this situation, the only force acting would be due to gravity, pushing down on each layer, without any sideways movement creating shear stress.
Gravity Forces and Pressure Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What the two forces we have? The gravity force and the force due to the pressure distribution. So whatever the pressure distribution forces that what is equate with the gravity force. Very simple things now, and since is a fluid is at the rest, so you can say that there is no mass flux is coming into the any control volumes or the momentum flux or no external work done it. So this is the what the simplified case.
Detailed Explanation
In a resting fluid, the only forces acting are due to gravity and pressure distribution. When we analyze these forces, we find that the pressure force must balance with the weight of the fluid acting under gravity. Since the fluid is at rest, there are no changes in mass or momentum within the control volume, simplifying our calculations because we are only focusing on these two forces.
Examples & Analogies
Imagine a swimming pool filled with water. The weight of the water exerts pressure against the bottom of the pool due to gravity. If you dive into the pool and notice how you feel the pressure increase as you go deeper, this is exactly how pressure distribution balances with gravity in a body of still water. Each layer of water below you feels the weight of all the layers above it.
Understanding Hydrostatics Through Examples
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Like for example, if you take this dam, which is 100-meter-high and we have a reservoir, let you consider this is what 90 meter height from the bottom. That is what the water levels is 90 meter from the bottom. And you can understand it because of these in the reservoirs the fluid is at the rest conditions and that rest condition exerting the pressures on these surface.
Detailed Explanation
In practical applications, such as with a dam or a tank, we need to understand how fluid pressure acts on surfaces due to hydrostatic conditions. Consider a dam that is 100 meters high with a water level of 90 meters. The pressure at different depths is not uniform; it increases with depth due to the weight of the water above, and this pressure must be considered when designing such structures to ensure they can withstand these forces.
Examples & Analogies
A real-world analogy could be a large aquarium. As you fill it with water, you can feel the pressure against the sides of the glass increasing the deeper you go. Just like the dam, the bottom of the tank experiences greater pressure due to the layers of water above it pushing down. If the aquarium were not designed to handle this pressure, it could break, leading to a spill—just like how a dam could fail if it doesn't account for pressure distribution from the water it holds.
Fluid as a Rigid Body Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Second thing is that fluid act as a rigid body motions. Let us take an example here that I have a tank which is a half filled liquid is there. Let us consider it may have water and this tank is accelerated with a constant acceleration a. As you start accelerating this tank with a constant acceleration a, you can understand it, this free surface is going to change it.
Detailed Explanation
When a fluid in a tank is accelerated, it behaves as if it were a rigid body in certain conditions. As the tank accelerates, the surface of the fluid adjusts to maintain equilibrium, forming a new surface angle depending on the acceleration. Even though the fluid is moving within the tank, there are no shear stresses acting within the fluid due to the uniform acceleration. Therefore, we can still apply the principles of hydrostatics to analyze the pressure distribution.
Examples & Analogies
Think about a car filled with water in a cupholder. If you accelerate the car quickly, the water will slosh to the back of the cup, forming a new surface. Here, the water inside is moving but still behaves according to hydrostatic principles; we can calculate the angle of the water surface and the pressure at different points accordingly, treating it as if the fluid is in a static condition relative to the tank's motion.
Applying Pascal’s Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now whenever I am talking about that I am looking for a pressure field as the fluid is at rest. So basically I am looking at the pressure is a function of the positions and time is not there, as the fluid is at rest condition.
Detailed Explanation
In hydrostatics, particularly when a fluid is at rest, we can express pressure as a function of position within the fluid. Since time is irrelevant in a static state, the pressure at a given point only depends on the vertical height of the fluid above that point. This principle leads to Pascal's Law, which states that pressure applied to any part of an incompressible fluid is transmitted undiminished throughout the fluid, meaning pressure is uniform in all directions.
Examples & Analogies
A classic example of Pascal's Law is seen in hydraulic systems, like car brakes. When you press down on the brake pedal (applying pressure), this pressure is transmitted through the brake fluid to activate the brakes on the wheels, showing how a small force can be magnified to create larger forces in the braking system, making it an essential feature of modern automotive design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatics: Study of fluids at rest.
-
Pascal's Law: Pressure applied to a fluid in a container is transmitted equally.
-
Pressure: Force per unit area exerted by a fluid.
-
Gauge Pressure: Pressure measured relative to atmospheric pressure.
-
Capillary Action: Rise of liquid in narrow tubes due to adhesion.
-
Hydrostatic Pressure: Pressure at a point in a fluid due to the weight of the fluid above.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of hydrostatic pressure is designing a dam where engineers calculate the pressure exerted by water against the dam walls.
-
Capillary action is observed when water rises in a thin straw, showing how adhesive forces can overcome gravity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fluid at rest, pressure best; pushing equal in all directions, no stress.
📖 Fascinating Stories
-
Imagine a quiet pond. The water is perfectly still, like students focused in class. Each drop of water feels the same pressure as neighboring drops, thanks to Pascal, our fluid friend!
🧠 Other Memory Gems
-
PUSH: Pressure Used Superbly Helps, to remember the benefits of hydrostatic pressure in engineering.
🎯 Super Acronyms
DIVE
- Depth Influences Vital Energy
- a: reminder that depth affects pressure in fluids.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The branch of fluid mechanics that studies fluids at rest.
-
Term: Pascal's law
Definition:
A principle stating that pressure applied to a confined fluid is transmitted undiminished in all directions.
-
Term: Pressure
Definition:
The force exerted per unit area within a fluid.
-
Term: Gauge pressure
Definition:
The pressure relative to atmospheric pressure.
-
Term: Capillary action
Definition:
The ability of a liquid to flow in narrow spaces without the assistance of external forces.
-
Term: Hydrostatic pressure
Definition:
The pressure exerted by a fluid at equilibrium due to the force of gravity.