Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatics
Unlock Audio Lesson
Welcome, everyone! Today, we'll start exploring fluid statics, which deals with fluids at rest. Can anyone tell me what you think happens to fluids when they are not moving?
I think they don't have velocity, so maybe their pressure behaves differently than in flowing fluids?
Exactly! The pressure in a fluid at rest is solely dependent on its depth and the density of the fluid. This leads us to Pascal's Law: the pressure is distributed uniformly throughout the fluid.
What does Pascal's Law say exactly?
Good question! Pascal's Law states that a change in pressure applied to an enclosed fluid is transmitted undiminished to every point of the fluid and to the walls of its container.
So, does that mean the pressure is the same at different points in the fluid?
Yes, provided the fluid is at rest, the pressure at each point depends only on the depth. Let’s summarize: fluids at rest have no velocity gradient, the pressure is uniform, and this leads us to understand fluid forces acting under gravity.
Applications of Hydrostatics
Unlock Audio Lesson
Now, let's see how hydrostatics applies in real life. Can anyone think of a scenario where understanding fluid pressure is crucial?
What about designing a dam? The pressure exerted by water depends on its height, right?
Exactly! The height of the water directly affects the pressure on the dam. This understanding helps engineers design structures capable of withstanding such pressures.
Does that also apply to things like oil tanks?
Yes, indeed! Similar principles apply to tanks, where we calculate the pressure exerted on the walls based on the fluid's height.
And I remember you mentioning something about barometers in our last lecture?
Correct! Barometers use hydrostatic pressure to measure atmospheric pressure, demonstrating the foundational role of hydrostatics in meteorology. Our key takeaway is: understanding how pressure functions at rest is vital for engineering applications.
Taylor Series and Pressure Calculations
Unlock Audio Lesson
Next, let's move on to how we can approximate functions related to pressure fields using Taylor series. Who here can explain what a Taylor series is?
I think it's a way to express functions as an infinite sum of terms calculated from the values of its derivatives at a certain point?
That's right! In our context, if we know the pressure at a certain point, we can estimate it at nearby points using this series. For incompressible fluids, we mainly consider the first-order terms.
So we neglect the higher-order terms since they contribute less?
Exactly! That simplification makes calculations much easier and keeps us focused on what significantly affects pressure. Can anyone give me an equation from this process?
I think it goes like this: P(x) = P₀ + ρgΔz?
Perfect! This equation captures how pressure changes with depth in a fluid, illustrating the principles we've discussed today. Let's recap: Taylor series simplify pressure calculations, and knowing how to apply these principles is crucial in fluid dynamics.
Understanding Pressure and Gravity Distribution
Unlock Audio Lesson
Now, let’s focus on the relationship between gravity and pressure distribution. Can anyone tell me how gravity influences fluid pressure?
Gravity pulls down on the fluid, so the deeper you go, the more pressure there is, right?
Exactly! The pressure at any point in a fluid depends not only on the fluid’s density but also on the gravitational force acting on it.
So, is that why we see differences in pressure in different heights when you look at lakes or oceans?
Yes, pressure increases with depth due to gravity. That leads us to important applications, such as hydraulic systems and their design. Remember this fundamental principle: pressure in a static fluid is always a result of the weight of the fluid above it.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the study of fluid statics is examined, particularly the behavior of fluids at rest. Key concepts include hydrostatic pressure, Pascal's law, and practical applications such as barometers and the capillary effect. The relationship between pressure and gravitational forces is also highlighted.
Detailed
Pressure Field Analysis
This section provides a comprehensive exploration of fluid statics, focusing on the behavior of fluids at rest. The discussion begins by contextualizing fluid mechanics principles and lists essential references for further reading. Key topics include:
- Hydrostatics: Fluids at rest are analyzed, where velocity vectors are zero, leading to the conclusion that gravitational forces and pressure distributions are the only forces acting.
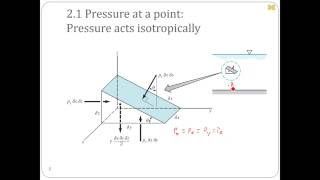
- Pressure Distribution: The section elaborates on how pressure varies across different fluid domains, introducing concepts such as gauge pressure, vapor pressure, and hydrostatic pressure distributions.
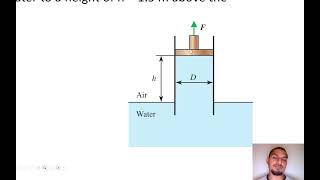
- Examples: A dam's design based on pressure acting on different surfaces and the principles applied to design oil tanks are provided.
- Pascal's Law: The principle that pressure within a static fluid is transmitted uniformly in all directions is explored.
- As fluids at rest do not exhibit shear stress due to a lack of velocity gradients, only normal stress is relevant, emphasizing the scalar nature of pressure in static fluids.
- Taylor Series Approximation: The pressure field is examined using Taylor series expansions to approximate pressure and velocity fields in terms of positional variables.
- Real-World Applications: The barometer for atmospheric pressure measurement and the capillary effect in liquids further illustrate hydrostatic concepts.
Through these discussions, the text emphasizes how understanding static fluid behavior is crucial for practical applications in engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid At Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now.
Detailed Explanation
When we refer to a fluid at rest, we're discussing a situation where the fluid is not moving. In this condition, the velocity of the fluid is zero, simplifying our analysis. Since there is no motion, we only need to consider how pressure varies within the fluid. Additionally, the density remains constant for incompressible fluids, which further simplifies our calculations.
Examples & Analogies
Imagine a glass of water sitting still on a table. Since the water is not moving, we can easily analyze the pressure at different depths in the glass using basic principles. The deeper you go, the greater the pressure due to the weight of the water above.
Shear Stress in Static Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress.
Detailed Explanation
In a static fluid, there is no change in velocity at different points, which means that there are no shearing forces acting on the fluid. Since shear stress arises from velocity gradients, a constant velocity (in this case, zero) means that shear stress is also zero. This allows us to conclude that when fluid is at rest, there are no shear stresses acting on any surfaces in contact with the fluid.
Examples & Analogies
Think of honey sitting in a jar. If you don't stir the honey, the layers remain evenly distributed with no sliding between them. This is similar to how pressure varies in a static system, where there's no movement causing any shear.
Forces Acting on a Fluid Element
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And what the two forces we have? The gravity force and the force due to the pressure distribution.
Detailed Explanation
When analyzing a fluid element at rest, we primarily consider two forces: the gravitational force acting downwards and the pressure force acting perpendicular to the surface. The pressure force is a result of the pressure distribution within the fluid, while gravity pulls the fluid down due to its weight. At equilibrium, these forces balance each other.
Examples & Analogies
Consider a swimming pool filled with water. At any given depth in the water, the pressure force from the water above balances the downward gravitational force. This equilibrium is essential for understanding how structures like dams and underwater pipelines function.
Hydrostatic Pressure Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Based on these the pressure load we can design this dam structure. That is what the examples for fluid at the rest.
Detailed Explanation
When dealing with hydrostatic pressure, engineers need to calculate how much pressure is exerted on surfaces by fluids at rest, such as in dams. This helps ensure that structures can withstand the forces applied without failing. The pressure increases with depth, governed by the equation P = ρgh, where ρ is the fluid density, g is gravity, and h is the height of the fluid.
Examples & Analogies
Like assessing how heavy water exerts pressure on the walls of a swimming pool, engineers use similar principles to calculate the pressure exerted by the water behind a dam wall, ensuring that the structure remains stable and safe.
Fluid as Rigid Body Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Second thing is that fluid act as a rigid body motions.
Detailed Explanation
In some cases, such as when a tank holding fluid is accelerated, the fluid behaves as if it were a rigid body. As the tank accelerates, the fluid surface will tilt, maintaining equilibrium while experiencing a pressure distribution similar to that found in static fluids. Even though the tank moves, there are no shear stresses acting in the fluid, allowing us to apply the principles of hydrostatics.
Examples & Analogies
Picture riding in a car that suddenly accelerates. You may feel yourself being pushed back into your seat due to the forces acting on you. Similarly, the fluid in the acceleration tank equally experiences forces but remains at rest relative to the tank and adjusts its free surface.
Pressure as a Function of Position
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now whenever I am talking about that I am looking for a pressure field as the fluid is at rest. So basically I am looking at the pressure is a function of the positions.
Detailed Explanation
In a fluid at rest, pressure varies depending on the position within the fluid, typically increasing with depth. Since the fluid is static, we can express pressure as a function of spatial variables (like height), eliminating time from consideration. Taylor series can be used to approximate pressure values at different heights, although in many cases, we focus on the primary term of the series, neglecting smaller contributions from higher order terms.
Examples & Analogies
Imagine measuring the pressure at different depths in a pool using a pressure gauge. At the surface, the pressure is lowest and gradually increases as you go deeper, reflecting how position affects the pressure experienced within the fluid.
Applying Pascal's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let come it to very basic law is called Pascal. As you when you fluid is rest let us consider is that the there will be a normal stress acting on any plane.
Detailed Explanation
Pascal's Law states that in a static fluid, pressure is transmitted equally in all directions. This means that if you apply pressure on a fluid in a confined space, that pressure will increase uniformly throughout the fluid. As we analyze a control volume, we can expect that the normal stresses due to pressure are equal in all directions, confirming that pressure is indeed a scalar quantity.
Examples & Analogies
Think of a balloon. If you squeeze it at one point, the pressure goes up throughout the entire balloon equally, demonstrating Pascal's Principle. This principle is vital in hydraulic systems where force applied in one area can be used to create a larger force elsewhere.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure Distribution: The distribution of pressure in a fluid depends on depth and fluid density.
-
Fluid at Rest: When a fluid is at rest, it has no velocity or shear stress, only pressure and gravitational forces acting.
-
Pascal's Law: Pressure change in an enclosed static fluid is transmitted uniformly in all directions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A dam's construction that accounts for pressure from water height, allowing engineers to calculate the necessary strength.
-
Barometers which measure atmospheric pressure based on hydrostatics principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids are still, pressure does fill, deeper you go, more force does show.
📖 Fascinating Stories
-
Imagine a dam holding back water. As more water fills behind it, the pressure at the bottom increases due to the weight of the water above, supporting the dam's base.
🧠 Other Memory Gems
-
P=ρgh: 'Pressure is density times gravity times height.'
🎯 Super Acronyms
H for Hydrostatic, P for Pressure, and D for Distribution.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces and pressures associated with them.
-
Term: Pascal’s Law
Definition:
A principle stating that a change in pressure applied to an enclosed fluid is transmitted uniformly in all directions.
-
Term: Gauge Pressure
Definition:
Pressure measured relative to atmospheric pressure.
-
Term: Vapor Pressure
Definition:
The pressure exerted by a vapor in equilibrium with its liquid or solid form.
-
Term: Hydrostatic Pressure Distribution
Definition:
The variation of pressure in a fluid at rest due to the weight of the fluid above a certain point.