Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Statics
Unlock Audio Lesson
Welcome, everyone! Today we will discuss fluid statics, which deals with fluids that are at rest. Can anyone tell me what happens to the velocity of a fluid in a statically considered system?
I think the velocity is zero since the fluid isn’t moving.
That's correct! When fluid is at rest, the velocity vectors are zero, and we only consider the pressure field. This leads to a simpler analysis. Why do you think understanding pressure in static fluids is important?
Because it helps in designing structures like dams and tanks!
Exactly! Understanding how pressure exerted by the fluid can affect these structures is crucial for engineers. Let’s dive deeper into pressure variations.
Pascal's Law
Unlock Audio Lesson
Now, let’s talk about Pascal's law. Who can explain what it states?
It says that pressure applied to a confined fluid is transmitted undiminished in all directions!
Exactly! This means that when you apply pressure to a static fluid, it spreads throughout the fluid evenly. Can anyone give a practical example of where we might see this in real life?
In hydraulic systems, right? Like car brakes!
Spot on! Hydraulic systems use this principle to amplify force. Keep that in mind as we look into real-world applications.
Pressure Distribution in Fluids
Unlock Audio Lesson
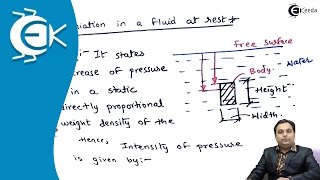
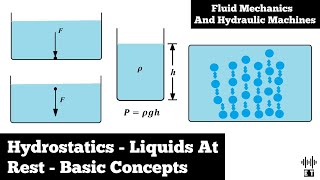
Let’s explore pressure distribution within a static fluid. Pressure increases with depth due to the weight of the fluid above. Can someone mathematically express this relationship?
I think it’s something like P = P₀ + ρgh, where P₀ is the surface pressure?
Correct! That’s the hydrostatic pressure equation. It shows how pressure changes as you go deeper in the fluid. Why do we consider the density (ρ) and gravity (g) here?
Because they both affect how much weight the fluid above presses down on the fluid below!
Exactly! This relationship is vital for calculating forces acting on submerged surfaces, such as dam walls.
Applications of Hydrostatics
Unlock Audio Lesson
Now that we understand pressure variations, let’s discuss some applications. How is this knowledge used in engineering, especially in dams?
We need to calculate how much pressure the water exerts on the dam walls based on its height and density!
That’s right! Engineers design dams by calculating these pressure forces to ensure structural integrity. Can anyone think of another application?
How about barometers? They measure atmospheric pressure!
Perfect! Barometers use the height of a column of mercury to measure pressure, reflecting the principles of hydrostatics. Let’s now summarize what we have learned.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore hydrostatic principles, including Pascal's law, pressure distributions, and the implications of fluid statics in practical situations such as dam design and pressure measurement. The chapter emphasizes the significance of understanding pressure variation in static fluids and its applications in engineering.
Detailed
Pressure Variations in Fluid at Rest
This section focuses on fluid statics, which deals with fluids that are not in motion. When considering liquids at rest, the primary variable of interest is pressure, as velocity gradients and shear stress are absent. The section explains how pressure is influenced by gravitational force, described by Pascal's law, which states that pressure applied to a confined fluid transmits uniformly in all directions. Important applications, such as determining pressure in dams and the behavior of fluids in rigid body motion, are discussed. Understanding these pressure variations is crucial for the design and assessment of hydraulic structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept of Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the very basic concept what we are talking about the fluid at rest. So the basically we are talking about now, the fluid at rest, okay? If it is a fluid is at rest, it is a very simplified problem now. Like as I said it any fluid flow problems we look at either the pressure field, the velocity field, or the density and temperature field. When the fluid is rest now, very simply way the velocity vectors becomes zero and if I consider incomprehensible the density is a constant and if the temperature is not very much I need not need a thermodynamics first laws to define the problems. Then only the left is that the pressure field.
Detailed Explanation
In fluid mechanics, when we say 'fluid at rest', we mean that the fluid is not moving. This simplifies the analysis greatly because if the fluid isn't moving, the velocity vectors are zero. In this scenario, we don't need to consider how velocity changes over time or space, simplifying our calculations. Generally, we analyze three main fields: pressure, velocity, and density. However, when a fluid is not moving (i.e., at rest), we focus only on the pressure field. Further, if we consider the fluid to be incompressible, the density remains constant which also simplifies our analysis. The temperature can usually be treated as a constant in basic fluid static problems.
Examples & Analogies
Consider a bucket of water sitting still on the ground. The water is not moving, so the speed of the water is zero. Because of this, the only thing we need to think about is the pressure exerted by the water on the bottom of the bucket, which comes from the weight of the water above it.
Shear Stress in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Since there is no velocity, there is no velocity gradient, definitely as Newton's second law says that there is no velocity gradients that means no shear stress. So when a fluid is at rest, there is no shear stress acting on that.
Detailed Explanation
In a fluid at rest, because there is no movement, it follows that there can be no changes in velocity within the fluid, which means there is no velocity gradient. According to Newton's second law, the absence of a velocity gradient means there is no shear stress being applied to the fluid. Shear stress occurs when layers of fluid move relative to each other, and since this isn't happening, we can say shear stress is zero. This simplification allows us to focus on pressure forces without worrying about shear forces, making calculations much easier.
Examples & Analogies
Think of a jar filled with honey that you leave untouched. The honey does not move, and consequently, no internal layers slide over each other. This absence of flow means there are no shear stresses causing the honey to change position, illustrating that in a stationary fluid, shear stress is effectively zero.
Pressure Forces and Gravity in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So you can take a surface or take a control volume. Over that control surface you can define it the shear stress components become zero. That is very simplified now that any control volume you consider it over that control volume surface as the fluid is at rest conditions, there is no shear stress acting on the control surface. So that is the very easy problems what we have now. And what the two forces we have? The gravity force and the force due to the pressure distribution.
Detailed Explanation
When we analyze a control volume (a specific region in space where we examine the behavior of fluid), we can simplify our analysis greatly since the shear stress is zero. In a fluid at rest, the only two forces acting on the control volume are the gravitational force pulling downward (due to the weight of the fluid) and the pressure force acting upwards (due to the pressure at the bottom of the control volume). This means we can balance these forces to understand how pressures behave throughout the fluid.
Examples & Analogies
Imagine a tall glass of water. The water exerts pressure on the bottom of the glass due to the weight of the water above it. At the same time, gravity is pulling down on the water. The balance between these two forces determines the pressure at any point within that glass.
Equilibrium and Simplifications in Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
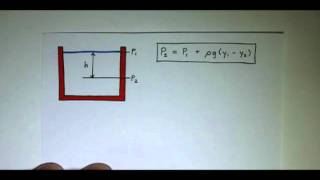
So we have just considered this fluid element or the control volumes at the equilibrium conditions. Similar way, rearranging the above equation gives P = P + ρgz.
Detailed Explanation
When we analyze a fluid at rest, we assume that it is in equilibrium, meaning all forces are balanced and there are no net movements. In hydraulics, we often express this equilibrium condition in terms of pressure change with depth, derived from the balance between gravitational force and pressure force. The equation P = P + ρgz indicates that the pressure at a certain depth (P) increases as you go deeper in a fluid, taking into account the weight of the fluid above it. This relationship is crucial in applications like calculating pressures in dams and underwater structures.
Examples & Analogies
This concept can be visualized if you think of diving underwater. As you swim deeper in a pool, you can feel the pressure increasing around you because more water is above you pressing down due to gravity. The formula demonstrates how that pressure increase relates to water depth.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Equilibrium: Condition where fluid in a system is not moving, and pressure varies with depth.
-
Pascal's Law: Describes how pressure is transmitted undiminished in an enclosed fluid.
-
Pressure Variations: Pressure increases linearly with depth due to gravitational force acting on the fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A dam experiences different pressure forces on its structure because of the varying water height—the deeper the water, the higher the pressure.
-
In a barometer, the height of mercury indicates atmospheric pressure, following the principles of hydrostatics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fluid at rest, pressure does grow, / Deeper you dive, more pressure you know.
📖 Fascinating Stories
-
Imagine a water balloon gently resting on the ground. When you apply pressure from the top, it evenly spreads out. This represents Pascal's Law in action.
🧠 Other Memory Gems
-
P(r)essure = D(eep) * G(ravity) * H(eight) helps remember the hydrostatic pressure formula.
🎯 Super Acronyms
P.H.D.
- P: = Pressure
- H: = Height of fluid
- D: = Density of fluid.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatics
Definition:
The branch of fluid mechanics that studies fluids at rest.
-
Term: Pascal's Law
Definition:
The principle that pressure applied to an enclosed fluid is transmitted uniformly in all directions.
-
Term: Gauge Pressure
Definition:
The pressure of a fluid measured relative to atmospheric pressure.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at equilibrium due to the gravitational force acting on it.