Assumptions for Fluid Flow Problems
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Steady Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's begin with the concept of steady flow. In a steady flow, the fluid's properties at any given point remain constant over time. This simplifies our equations.

Does that mean the velocity doesn't change?

Exactly! If the flow is steady, the velocity at a point remains the same over time. Can anyone help me remember what 'steady' means in terms of fluid properties?

Steady means it does not change over time!

Great! Now, how does this apply to our control volumes?

It means we can just focus on surface integrals instead of dealing with complicated derivatives!

Exactly! Remember, if we visualize steady flow, we can often simplify our equations significantly.
Incompressible Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's discuss incompressible flow. This assumption states that the density of the fluid remains constant throughout.

So, does that apply to all fluids?

Not exactly. In incompressible flow, we often assume this applies to liquids, like water, under normal conditions. What does this imply for our equations?

We can take density out of the equations?

Correct! This allows us to simplify our integrals significantly. Now, in what real-life situations can we see this assumption at play?

When analyzing water flow in pipes!

Right! Good examples help keep these concepts relevant.
Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's move on to control volumes. We categorize them into three types: fixed, moving, and deformable. What can anyone tell me about fixed control volumes?

They're stationary and stay in the same location!

Yes! And what about moving control volumes?

Those move, like a ship in water!

Excellent! Lastly, the deformable control volume - what distinguishes it from the other two?

It can change shape over time!

Correct! Understanding these distinctions is vital for applying fluid mechanics.
Application of Assumptions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's apply what we've learned. For instance, in the Mars Orbiter Mission, how do we see these assumptions being critical?

They would have to calculate the trajectory considering steady flow!

Exactly! And ignoring compressibility in that scenario would simplify the calculations. Can anyone think of other applications?

Designing water supply systems!

Great example! Understanding fluid properties allows engineers to create efficient systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Fluid flow problems require certain assumptions for effective analysis. This section focuses on steady and incompressible flows, along with the implications for mass conservation and control volumes.
Detailed
Assumptions for Fluid Flow Problems
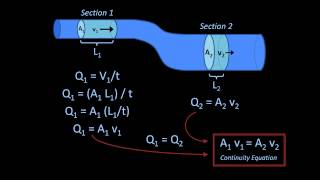
In fluid mechanics, specific assumptions about the flow of fluids are essential for simplifying complex problems. Two predominant assumptions discussed are steady flow and incompressible flow. Steady flow implies that the fluid's properties at a particular point remain constant over time, which simplifies the analysis by eliminating time-dependent variables. Incompressible flow assumes that the fluid density remains constant throughout the analysis.
These assumptions lead to crucial equations, like the conservation of mass, which operates under the form of the Reynolds transport theorem. Specifically, by applying these assumptions, complexities with partial derivatives can be reduced, focusing on surface integrals across control surfaces. This is further exemplified through different types of control volumes, including fixed, moving, and deformable control volumes, each addressing different real-world fluid dynamic situations.
Furthermore, various applications, such as fluid flow in ships and satellite trajectories, highlight the significant impact of these assumptions in engineering designs and real-life problems.
Youtube Videos
![Common assumptions in fluid mechanics [Fluid Mechanics #3b]](https://img.youtube.com/vi/kimMbNP9DrY/mqdefault.jpg)







![The Ideal Fluid Model [Physics of Fluid Mechanics #39]](https://img.youtube.com/vi/L8CxMeMR9oc/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Relative Velocity in Moving Control Volumes
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
For moving control volumes like ships, we need to consider relative velocity—the difference between the fluid velocity and the control volume's velocity. This is important for accurately calculating flow rates across the control surface.
Detailed Explanation
When dealing with flow in moving control volumes, such as a ship in water, understanding how quickly the water flows concerning the ship becomes crucial. This is termed 'relative velocity.' The fluid velocity (how fast the water moves) is adjusted by how fast the ship itself moves, which can make the fluid appear to flow faster or slower to an observer on the ship.
If a ship moves forward at 3 m/s and the water flows at 5 m/s against it, the water’s speed relative to the ship is 2 m/s.
Examples & Analogies
Think of riding a bicycle downstream in a river. If you’re pedaling at 5 km/h and the river flows at 3 km/h toward your direction, you might feel like you’re moving at 8 km/h with respect to the riverbank, but only at 2 km/h with respect to the water. This concept is essential to determine effective motion in fluid mechanics.
Effects of Deforming Control Volumes
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If a control volume is both moving and deformable, the velocity changes not only with time but with position as well. This adds complexity since both fluid and control volume velocities are functions of position and time.
Detailed Explanation
When analyzing deforming control volumes, such as air currents flowing around a moving object that is also changing shape (like an airplane wing), the velocities must be treated variably. Both the fluid's speed and the control volume's shape change at different points and times, requiring a more complex analysis. This makes calculations more complicated since each point in the flow has varying velocity based on its position and time.
Examples & Analogies
Imagine a droplet of water falling on a waving surface. As the water droplet falls, it encounters a surface that is moving in different directions—this creates varying speeds and directions of flow around it. The shapes and motions of both the droplet and surface are constantly changing, making it a real challenge to predict where the droplet will go next. This is a perfect analogy for how a deforming control volume can complicate fluid dynamics calculations.
Key Concepts
-
Steady Flow: Properties remain constant over time.
-
Incompressible Flow: Density remains constant.
-
Control Volumes: Defined regions for analysis of fluid flow.
Examples & Applications
Analyzing the flow of water in an irrigation system as an incompressible flow.
Studying air flow around a moving aircraft as a steady flow problem.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Steady flow is quite the show, no changes here, just let it go.
Stories
Imagine a river flowing steadily, where the water doesn't change its pace, representing steady flow. It moves smoothly, never changing direction or density, exemplifying incompressible flow.
Memory Tools
Control volumes can be remembered by the acronym 'FMD': Fixed, Moving, Deformable.
Acronyms
SIM
Steady Incompressible Motion describes the essence of these flow assumptions.
Flash Cards
Glossary
- Steady Flow
A flow in which properties at a point do not change over time.
- Incompressible Flow
A flow assumption where the fluid density remains constant.
- Control Volume
A defined region in space through which fluid flows, used to analyze fluid behavior.
- Reynolds Transport Theorem
A theorem that relates changes in a system to changes in a control volume.
Reference links
Supplementary resources to enhance your learning experience.
