Control Volume and Reynolds Transport Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss control volumes. Can anyone tell me what a control volume is?

Is it a defined region in space where we analyze fluid flow?

Exactly! Control volumes help us analyze the behavior of fluids. Now, why do you think the Reynolds transport theorem is important?

It relates the changes in a system to flow across a control surface, right?

Correct! The theorem establishes a crucial relationship between system dynamics and control volume analyses.
Types of Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can anyone name the three types of control volumes?

I think there are fixed, moving, and deformable control volumes.

That's right! Can you explain each type briefly?

A fixed control volume stays in one place, a moving control volume moves with the fluid, and a deformable control volume can change shape.

Excellent summary! Each type has applications in real-world fluid problems.
Deriving Mass Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's talk about how we can derive the conservation of mass equation. What factors do we consider?

We need to look at mass influx and outflux across the control surface.

Exactly! And what is the implication of the mass conservation principle?

The net mass change inside the control volume is equal to the mass flowing into and out of it.

Correct! This principle applies to incompressible flows.
Practical Applications of Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Can anyone give an example of fluid mechanics application?

The Mars Orbiter Mission uses fluid dynamics to calculate trajectories.

Great example! How does fluid mechanics aid in such missions?

It helps in understanding drag forces and trajectories during the satellite's launch.

Exactly! Fluid dynamics is critical in ensuring successful missions in space.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the relationship between systems and control volumes through the Reynolds transport theorem, detailing the types of control volumes and their relevance in fluid mechanics. We focus primarily on mass conservation equations and practical applications.
Detailed
Control Volume and Reynolds Transport Theorem
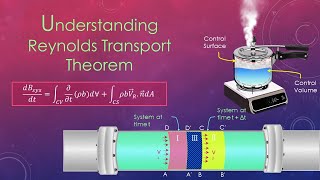
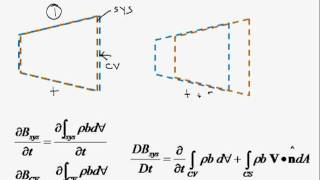
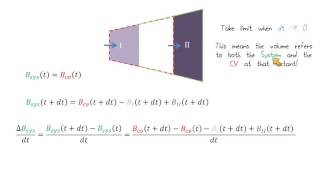
In this section of fluid mechanics, the focus is on the Reynolds transport theorem, vital for deriving the conservation of mass equation. The differences between system and control volume are discussed, emphasizing that fluid mechanics largely relies on control volume perspectives. The section categorizes control volumes into three types: fixed control volume (stationary in space), moving control volume (like a ship in water), and deformable control volume (where the shape can change).
The derivation process for the conservation of mass is outlined, emphasizing that mass influx and outflux across control surfaces play a critical role. Furthermore, it explains how Reynolds transport theorem relates extensive and intensive properties at both system and control volume levels. The section elaborates on steady versus unsteady and compressible versus incompressible flows, simplifying the mathematics involved in fluid flow problems. Practical examples such as the Mars Orbiter Mission illustrate the necessity of fluid mechanics in real-world applications, showcasing how knowledge of fluid dynamics aids in complex trajectory calculations involving fluid forces.
The core takeaway is that mass conservation remains essential in fluid mechanics, aligning mass influx and outflux within control volumes, crucial for solving practical fluid flow issues.
Youtube Videos




![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Control Volumes
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us come back to what we learned in the last class. If you remember it, I discussed very thoroughly what is the difference between systems and the control volume. Mostly in fluid mechanics we follow the control volume aspect. That is the reason we need a relationship between the system and the control volume. The Reynolds transport theorems establish the relationship of conversions of mass from system to control volume.
Detailed Explanation
In fluid mechanics, the concept of 'control volume' is crucial. A control volume is a specific region in space through which fluid can flow. The main idea behind using control volumes is to analyze how mass and energy enter and leave this defined space. This is different from the concept of a 'system', which could be more rigid and not necessarily change in a fluid dynamic context. The Reynolds transport theorem helps us understand how quantities like mass are conserved as they pass in and out of the control volume.
Examples & Analogies
Imagine a water tank with an inlet pipe and an outlet pipe. The tank itself acts as the control volume. Water flowing in through the inlet and out through the outlet represents the mass entering and exiting the control volume. By analyzing this tank, we can understand how much water (mass) is in the tank at any given time.
Types of Control Volumes
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, that is the strength of the Reynolds transport theorems and, as already I discussed, you can have three type of control volumes, fixed control volume, that means with reference to the space it remains at the same location. As the time goes, it does not move it. That is what fixed control volume is. It has definite control surfaces. The other one is moving control volume, like the ship movement in a sea or the river. The ship and the adjacent fluid can be considered as moving control volume. And we solved many of the problems with moving control volume, considering this control volume is moving with a particular velocity. Not only that, the shape of the control volume can change. That was the deformable control volume. The shape of the control volume can change with respect to time, then we call it deformable control volume. So, there are three types of control volume, fixed control volume, moving control volume, and deformable control volume.
Detailed Explanation
There are three primary types of control volumes in fluid mechanics:
1. Fixed Control Volume: This volume does not change position over time. It is useful for analyzing flows around stationary objects, such as a building in a wind tunnel.
2. Moving Control Volume: In this case, the control volume moves with the fluid, which is common in applications like ships navigating through water. The control volume travels along with the fluid, allowing for analysis of dynamic interactions.
3. Deformable Control Volume: This type can change its shape over time, adjusting to fluid flow dynamics. An example of this could be the deformation of an airfoil as it moves through air.
Understanding these types helps in choosing the right approach when applying the Reynolds transport theorem.
Examples & Analogies
Think of a fixed control volume as a swimming pool that doesn't change size or position. A moving control volume would be like a diver performing flips in mid-air, where the diver and the surrounding air act as the control volume, moving dynamically together. A deformable control volume can be visualized as a balloon being squeezed or stretched while being inflated, changing shape as more air enters.
Conservation Equations Using Control Volumes
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, as I have given very briefly Reynolds transport theorems and moving and deformable control volume, conservation of mass we will derive for simple case to complex problems, how we can write conservation of mass. Then, we will talk about some examples, real life examples we will take and how the appropriate choosing of control volume and the control surface can solve many of our problems.
Detailed Explanation
The conservation of mass is a fundamental principle in fluid mechanics, describing how mass cannot be created or destroyed in a closed system. When applying this to control volumes, the Reynolds transport theorem allows us to express mass conservation as an equation that states: the rate of change of mass within a control volume is equal to the mass inflow minus the mass outflow. This relationship can be used to set up equations for both simple and complex fluid flow situations, helping to model real-life scenarios such as pipeline flow, aerodynamics, or even natural phenomena.
Examples & Analogies
Consider a bucket being filled with water while simultaneously draining water from a hole at the bottom. By applying conservation of mass, we can calculate how fast the bucket fills or empties. If water flows in at 2 liters per minute through the top and out at 1 liter per minute through the drain, we can determine the net inflow to see how long it takes to fill the bucket.
Applications of Fluid Mechanics Principles
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let us go to very interesting applications. As you know it Indian Space Research Organisation launched the satellite which is called MOM programmes, that means Mars Orbiter Mission programme. But if you look at this, it is the fluid flow problem. If we look at the trajectory which is started from the earth, and if you look at the trajectory part here, how this trajectory goes on changing, which was launched on December 1, 2013, okay?
Detailed Explanation
The Mars Orbiter Mission (MOM) is an excellent example of advanced fluid mechanics in action, particularly in the areas of aerodynamics and trajectory optimization. When launching a satellite, engineers must carefully consider factors like atmospheric drag, propulsion forces, and the controlling of the satellite’s path as it travels from Earth to Mars. Fluid mechanics principles are essential in calculating the optimal force applications and trajectory paths to successfully navigate the satellite through varying conditions of the atmosphere and space.
Examples & Analogies
Think of launching a ball into the air. Just like how you would need to angle the throw to ensure it reaches its target, engineers must calculate the exact angle and speed for the rocket to escape Earth's gravity and travel to another planet. With MOM, every calculation is so precise that it safely reached Mars after executing multiple maneuvers, resembling a perfectly thrown ball landing where intended.
Key Concepts
-
Control Volumes: A conceptual tool in fluid mechanics for analyzing fluid behavior in a defined region.
-
Reynolds Transport Theorem: A theorem that links system dynamics to mass transfer across control surfaces.
-
Types of Control Volumes: Fixed, moving, and deformable—each used in different contexts.
-
Mass Conservation: Fundamental principle stating that mass inflow and outflow must balance in a control volume.
Examples & Applications
A ship sailing down a river can be modeled using a moving control volume.
The derivation of mass conservation equations can help predict flow rates in pipeline systems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a flow so grand, control volumes stand, to understand, where fluids expand.
Stories
Imagine a ship sailing down a river; it represents a moving control volume, influencing the water, from waves to currents.
Memory Tools
C-M-F: Control, Mass, Flow — remember the trio for fluid analysis!
Acronyms
R-T-T
Reynolds Transport Theorem — guiding us through fluid dynamics.
Flash Cards
Glossary
- Control Volume
A fixed or moving volume in space through which fluid flows, used to analyze fluid behavior.
- Reynolds Transport Theorem
A mathematical statement that connects the change in a quantity for a system to the flow of that quantity across its control surface.
- Mass Influx
The mass flow entering a control volume through its control surface.
- Mass Outflux
The mass flow exiting a control volume through its control surface.
- Conservation of Mass
The principle that mass is neither created nor destroyed; the mass change in a system is equal to mass inflow minus mass outflow.
Reference links
Supplementary resources to enhance your learning experience.
