Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Overview of Fluid Mechanics and Mass Conservation
Unlock Audio Lesson
Welcome class! Today, we will talk about mass conservation in fluid mechanics. Can anyone tell me why conserving mass is important?
I think it's important because it helps us understand how fluids behave in different contexts, right?
Exactly! Mass conservation ensures that the mass flowing into a control volume equals the mass flowing out. This is critical for analyzing fluid systems.
How do we derive the mass conservation equation?
Great question! We use the Reynolds transport theorem as our starting point.
Think of it as an acronym—R for 'Reynolds', T for 'Transport', establishing connections between systems and control volumes. RT helps us derive important equations like this one.
Are there different types of control volumes we should consider?
Yes! We have fixed, moving, and deformable control volumes, and each has a unique impact on fluid behavior. Let’s explore these further.
In summary, today we covered the basics and the significance of mass conservation in fluid mechanics.
Control Volumes and Reynolds Transport Theorem
Unlock Audio Lesson
Now, let’s dive deeper into the control volumes. Who can remind me what a fixed control volume is?
A fixed control volume stays in one position as time passes, right?
That's correct! Now, what about a moving control volume?
It moves with the fluid, like a ship on water!
Exactly! Now, how does the Reynolds transport theorem apply to these volumes?
It helps relate the system properties to those of control volumes, right?
Absolutely! This relationship is essential for establishing mass conservation. Remember the RT acronym—Reynolds Transport!
To summarize, we discussed the types of control volumes and their relevance to the Reynolds transport theorem.
Applications of Mass Conservation
Unlock Audio Lesson
Let’s connect these concepts to real-world examples. Can anyone think of an application of mass conservation?
What about fluid systems in engineering, like water treatment plants?
Great example! Water entering and leaving treatment plants must follow mass conservation principles to ensure proper functioning.
What about the launch of satellites? I remember you mentioned something about fluid mechanics and satellites.
Yes! The trajectory of satellites relies on precise calculations of fluid dynamic principles, where mass conservation plays a key role.
That's fascinating! Where else can it be applied?
From aerospace to environmental engineering, mass conservation is vital. In summary, we explored several applications highlighting the importance of mass conservation in engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The steady flow mass conservation equation is derived from the Reynolds transport theorem, which establishes a relationship between system and control volume. The section details different types of control volumes—fixed, moving, and deformable—and their implications for fluid flow analysis, ultimately leading to a broader understanding of mass flux in engineering applications.
Detailed
Steady Flow Mass Conservation Equation
This section delves into the derivation and application of the steady flow mass conservation equation within the field of fluid mechanics. The foundation of this equation lies in the Reynolds transport theorem, which relates the properties of a system to those of a control volume. The mass conservation equation, expressed in terms of control volume analysis, is crucial for solving fluid flow problems in practical engineering scenarios.
Key Concepts Covered
- Reynolds Transport Theorem: A critical concept that establishes the relationship between system properties and control volume properties over time.
- Types of Control Volumes:
- Fixed Control Volume: Does not change with time or moves; remains stationary in space.
- Moving Control Volume: Moves with a certain velocity, as seen with ships in fluid bodies.
- Deformable Control Volume: Its shape changes over time, allowing for dynamic fluid flow analysis.
The section presents several examples illustrating real-world applications, such as fluid flow for satellite trajectories, further emphasizing the significance of understanding mass conservation derived from the aforementioned principles. Moreover, distinctions between steady and unsteady flow conditions, along with compressible and incompressible flow scenarios, are discussed, showcasing their influence on practical problem-solving approaches. Ultimately, the mass conservation equation serves as a fundamental pillar in fluid mechanics education and practice.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
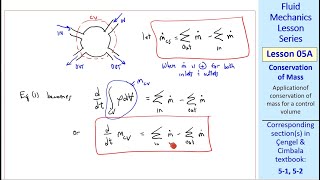
As I said earlier, when you have the control volume, through the control surface there is, mass influx coming into the control volume, going out from the control volume. Similar way, momentum flux comes into the control volume, also goes through the other surface as momentum flux going out from that. Similar way, we can think this energy flux comes into the control volume and goes out of this thing.
Detailed Explanation
This chunk introduces the concept of mass conservation in a control volume. A control volume is a defined region in space where we analyze the behavior of fluids. In this context, the mass influx refers to the mass entering the control volume through its control surface, and the mass outflux refers to the mass leaving it. Additionally, the flow of momentum and energy is discussed, indicating that similar conservation principles apply. Essentially, mass conservation means that the mass flowing into the control volume should equal the mass flowing out, assuming there are no additional mass sources within the volume.
Examples & Analogies
Imagine a water tank filled with water through a pipe. As water flows into the tank, it should also flow out through another pipe at the bottom, maintaining a steady level. If more water enters than exits, the tank fills up (i.e., an increase in mass storage), and vice versa. This water tank scenario illustrates the principle of mass conservation, where the amount of water in the tank remains balanced depending on the flow rates.
Deriving the Conservation of Mass Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at this equation, let us look it. This is the system level equations. This is what is at the control volume level. So, one talks about how this particular mass or momentum flux is crossing through the control surface.
Detailed Explanation
In this part, the lecture discusses the derivation of the mass conservation equation, distinguishing between system-level and control volume-level equations. The mass conservation equation relates the rate of change of mass within the control volume to the mass flux across its control surfaces. At steady state, the equation simplifies, typically showing that the mass entering the volume equals the mass leaving it. The lecturer emphasizes recognizing how mass and momentum fluxes cross through control surfaces — the mathematical foundation that leads to the conservation principles used in fluid mechanics.
Examples & Analogies
Consider a bus moving with passengers getting on and off at various stops. Each time a passenger enters the bus, it's equivalent to an influx of mass, and when a passenger exits, it's an outflux. By tracking how many passengers get on and off, we ensure that the total number of passengers is accounted for, similar to ensuring that mass conservation is maintained in our fluid control volume.
Steady and Incompressible Flow Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look if I have the velocity vectors, okay? Let us consider I have a control surface like this. If the n vector is like this, the perpendicular vector to the control surface is like that, if I consider one simple case, the velocity is either parallel or opposite.
Detailed Explanation
This chunk covers the assumptions we make for steady and incompressible flow while deriving the mass conservation equation. Steady flow means that fluid properties at any point do not change over time. Incompressible flow assumes that the fluid density remains constant. Under these conditions, the conservation of mass can be simplified because the density does not vary. The lecturer talks about velocity vectors' interactions with control surfaces, clarifying that if the normal vector (n) of the control surface is aligned with the fluid velocity, calculations become simpler since only the scalar product of velocities needs consideration.
Examples & Analogies
Imagine you have a smooth water slide (control surface) and water (fluid) flowing down it. If the slide is straight (fixed surface) and the water flows consistently, the speed of the water remains the same (steady). If it were splashing out (density variation), calculation would become more complex. Thus, the streamlined slide shows how steady and incompressible flow works together, resulting in easier mathematical descriptions.
Continuing the Derivation: Control Volume Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now coming to a very interesting (()) (13:15) if I consider moving control volume like a ship which is moving with a velocity V. So, then, the concept will be the same. Only here we will talk about the relative velocity component.
Detailed Explanation
This section shifts the discussion towards moving control volumes, such as a ship in motion. The key point is that when analyzing a control volume that itself is in motion, we need to consider the relative velocity between the fluid and the control volume. The relative velocity is the difference between the velocity of the fluid and the velocity of the control volume itself. This concept allows us to apply the steady flow mass conservation principle while accounting for the motion of the control volume, making it necessary to adjust our calculations for fluid entering or leaving it.
Examples & Analogies
Think about a swimmer in a flowing river. If the swimmer moves upstream against the current, their speed relative to the river bank is their swimming speed minus the river speed. To calculate how much water flows past them while swimming, we must consider this relative speed, just like we must consider the relative velocity in moving control volumes for accurate mass conservation calculations.
Final Thoughts on Conservation Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The net change of the mass in this control volume should be equal to the change of mass storage within the control volume. That is what the concept is you are looking at?
Detailed Explanation
The final part of the discussion reinforces the fundamental concept of mass conservation: the net change of mass in a control volume should equal the change in mass stored within that volume over time. For steady-state flow, this means that the mass entering the control volume equals the mass exiting. If there's no accumulation or depletion of mass over time in the control volume, the inflow and outflow must balance out. This principle is crucial for solving a wide range of practical problems in fluid mechanics.
Examples & Analogies
Consider a bank account where you deposit and withdraw money. If you continuously deposit the same amount that you withdraw, your account balance remains unchanged (like steady flow). In fluid mechanics, the principle is the same: the mass that flows in equals the mass that flows out, maintaining balance over time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorem: A critical concept that establishes the relationship between system properties and control volume properties over time.
-
Types of Control Volumes:
-
Fixed Control Volume: Does not change with time or moves; remains stationary in space.
-
Moving Control Volume: Moves with a certain velocity, as seen with ships in fluid bodies.
-
Deformable Control Volume: Its shape changes over time, allowing for dynamic fluid flow analysis.
-
The section presents several examples illustrating real-world applications, such as fluid flow for satellite trajectories, further emphasizing the significance of understanding mass conservation derived from the aforementioned principles. Moreover, distinctions between steady and unsteady flow conditions, along with compressible and incompressible flow scenarios, are discussed, showcasing their influence on practical problem-solving approaches. Ultimately, the mass conservation equation serves as a fundamental pillar in fluid mechanics education and practice.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The trajectory of the Mars Orbiter Mission exemplifies mass conservation in aerospace applications.
-
Water treatment plants utilize mass conservation to maintain balance between inflow and outflow for effective water treatment.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids that flow, mass must stay, inflow equals outflow, that's the way!
📖 Fascinating Stories
-
Imagine a river where fish swim upstream towards a fixed rock. The fish represent mass that flows seamlessly through the control volume—maintaining a balance between the upstream and downstream flow!
🧠 Other Memory Gems
-
Remember 'RT' for 'Reynolds Transport'—a tool to derive the equations governing fluid flows.
🎯 Super Acronyms
Use MCF for 'Mass Conservation Factor' to remember that mass must always balance!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Mass
Definition:
A principle stating that mass cannot be created or destroyed in an isolated system.
-
Term: Control Volume
Definition:
A defined region in space through which fluid can flow, utilized for analysis in fluid mechanics.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change in an extensive property of a system to the flow across the control volume boundaries.
-
Term: Fixed Control Volume
Definition:
A control volume that does not move with respect to space.
-
Term: Moving Control Volume
Definition:
A control volume that moves with the flow of fluid.
-
Term: Deformable Control Volume
Definition:
A control volume where the shape can change over time.