Types of Control Volumes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, let's talk about control volumes. What do you think a control volume is in fluid mechanics?

Is it a specific area in a fluid we are analyzing?

Absolutely! A control volume is a defined region in space where we analyze mass, momentum, and energy. Now, can anyone identify the different types of control volumes?

I think there are fixed and moving control volumes?

Correct! There are fixed control volumes, moving control volumes, and deformable control volumes. Let’s take a deeper dive into what each type entails!
Fixed Control Volume
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

First, let’s discuss the fixed control volume. What makes it unique?

It stays in the same place, right? So the boundaries don’t change over time.

Exactly! Fixed control volumes don’t change location or size. They provide clear boundaries to analyze fluid properties within this static region. Can anyone think of a practical example?

Maybe something like a reservoir that doesn’t move?

That's a great example! Reservoirs can be analyzed as fixed control volumes due to their stationary nature. This allows us to apply conservation laws easily.
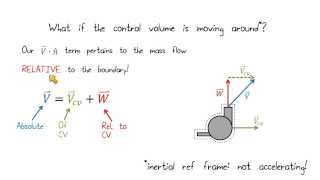
Moving Control Volume
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next up is the moving control volume! What do we mean by this?

It moves along with the fluid, like how a ship moves through water.

Exactly! The motion of the control volume can be the same as the fluid flow, or it can differ. What are some considerations we need to think about with moving control volumes?

Maybe how the velocities of the fluid affect the analysis?

Right! We must consider the relative velocities when applying equations like the Reynolds transport theorem, which connects system and control volume analyses. Good work!
Deformable Control Volume
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Finally, let’s examine deformable control volumes. How do these differ from the others we've discussed?

They can change shape over time while still being a part of the same control space?

Correct! The boundaries can shift based on fluid dynamics around them. This adaptability allows for a more accurate representation of varying conditions, such as in compressible flow scenarios. Why do you think this might be important?

Because real-world fluid systems often change shape, like in specific flow situations?

Exactly, this flexibility plays a vital role in analysis for complex flows!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we understand the distinctions between fixed, moving, and deformable control volumes as they apply in fluid mechanics. It emphasizes the relevance of these concepts in deriving mass conservation equations using the Reynolds transport theorem.
Detailed
Detailed Summary
In fluid mechanics, control volumes are critical for analyzing fluid flow through defined regions. This section discusses the three primary types of control volumes:
- Fixed Control Volume: A stationary volume in a fixed position over time, maintaining its boundaries regardless of the fluid flow.
- Moving Control Volume: This type follows a specific motion, such as a ship moving in water. The volume moves with it, and both the fluid and the control volume have velocities that may differ.
- Deformable Control Volume: This volume can change shape or size over time, adapting its boundaries to the flow characteristics around it.
Understanding these distinctions helps establish relationships between systems and control volumes using the Reynolds transport theorem, which crucia
lly informs the formulation of conservation equations in fluid mechanics, especially the conservation of mass, momentum, and energy. Such understanding is essential for effectively solving fluid flow problems, as the choice of control volume will influence the complexity of the analysis required.
Youtube Videos
![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, we follow the control volume aspect. That is the reason we need a relationship between the system and the control volume. The Reynolds transport theorem establishes the relationship of conversions of mass from system to control volume.
Detailed Explanation
In fluid mechanics, understanding the flow of fluids is essential. One way to study fluid flow is by defining a 'control volume,' which is a specified region in space where we analyze the mass and energy interactions. The control volume can represent the entire system or a part of it. The Reynolds transport theorem provides a mathematical relationship that helps us convert properties of a system (an object or region) to a control volume perspective, allowing us to analyze the mass transfer effectively.
Examples & Analogies
Consider a swimming pool (the control volume) where you are pouring water from a bucket (the system). The bucket has a certain amount of water. When you pour it into the pool, you can use the Reynolds transport theorem to understand how the amount of water in the bucket relates to changes in the pool's volume.
Fixed Control Volume
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Fixed control volume means it remains at the same location. As time goes, it does not move. It has definite control surfaces.
Detailed Explanation
A fixed control volume is an area in space that does not change its position over time. It allows us to analyze fluid flow without having to consider any translations or rotations. This is useful in scenarios where we want to analyze the flow into or out of a static region, such as a pipe or tank where fluid enters and exits without changing the observer’s position.
Examples & Analogies
Imagine a water tank. If we observe how much water is entering or leaving, we can define our control volume as the tank itself. As long as we are analyzing the water that is in the tank, we are using a fixed control volume.
Moving Control Volume
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Moving control volume refers to cases like a ship moving in water. The ship and the adjacent fluid can be considered as a moving control volume.
Detailed Explanation
In contrast to a fixed control volume, a moving control volume is one that changes its position over time. This scenario often occurs with vehicles in motion, such as ships or airplanes. In this case, we need to consider the relative motion of the fluid concerning the control volume, which makes the analysis slightly more complex, particularly in determining how mass and momentum are transferred across the control surfaces.
Examples & Analogies
Think of a ship sailing through water. The ship itself is a moving control volume, and as it travels, the water around it is also in motion. From the perspective of someone on the ship, they might need to analyze how much water is being pushed aside as they move forward, which connects the concepts of fluid dynamics to real-life situations.
Deformable Control Volume
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Deformable control volume means the shape of the control volume can change with respect to time.
Detailed Explanation
A deformable control volume is one in which the shape itself can change over time. This is encountered in systems where fluid interfaces shift or where the boundaries can expand and contract. Analyzing this type of control volume often requires consideration of how fluid properties and mass flow change due to deformation.
Examples & Analogies
An excellent example of a deformable control volume is a balloon. As you blow air into a balloon, the shape of the balloon changes. The control volume defined by the balloon's boundary is deformable because it expands as more air fills it up. This concept highlights how fluid dynamics can also relate to everyday objects like balloons.
Summary of Control Volume Types
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In summary, there are three types of control volumes: fixed control volume, moving control volume, and deformable control volume.
Detailed Explanation
In fluid mechanics, understanding the distinctions between different types of control volumes is crucial for solving problems related to fluid flow. Each type serves a different purpose and are used based on the conditions of the fluid system being analyzed. Recognizing whether to use a fixed, moving, or deformable control volume simplifies the equations and approaches used.
Examples & Analogies
Consider multiple vehicles on a race track: a parked car (fixed control volume), a car in motion (moving control volume), and a rubber tire bending as it rolls (deformable control volume). Each vehicle represents a different control volume technique applicable under fluid mechanics, showing how these concepts connect to dynamic environments.
Key Concepts
-
Fixed Control Volume: A control volume that remains in a fixed location in space.
-
Moving Control Volume: A control volume that travels with the fluid.
-
Deformable Control Volume: A control volume that can change shape and size over time.
-
Reynolds Transport Theorem: Essential theorem for deriving conservation equations.
Examples & Applications
An example of a fixed control volume is a water reservoir that does not change position while analyzing fluid flow.
An example of a moving control volume is a ship navigating through water with a varying fluid flow around it.
An example of a deformable control volume is a balloon filled with air that changes size as it is compressed.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In fluid treat, control volumes greet, fixed like a tree and moving so free!
Stories
Imagine a ship navigating a river. The river with its flow represents a moving control volume, while a bridge above represents a fixed control volume, and a balloon floating represents a deformable control volume.
Memory Tools
F-M-D: Fixed, Moving, Deformable - remember these types of control volumes!
Acronyms
C.V.M. - Control Volume Mechanics!
Flash Cards
Glossary
- Control Volume
A defined region in space used to analyze mass, momentum, and energy within fluid mechanics.
- Fixed Control Volume
A control volume that remains stationary in space and time, unaffected by fluid flow.
- Moving Control Volume
A control volume that travels with the fluid, often with its own velocity, influencing the analysis.
- Deformable Control Volume
A control volume that can change shape and size over time, adapting to fluid dynamics.
- Reynolds Transport Theorem
A theorem that provides the relationship between the time rate of change of a system and a control volume, especially useful in deriving conservation equations.
Reference links
Supplementary resources to enhance your learning experience.
