Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conservation of Mass
Unlock Audio Lesson
Welcome class! Today, we will delve into an important principle in fluid mechanics: conservation of mass. Can anyone tell me what that means?
Is it about how mass can't just disappear or appear out of nowhere?
Exactly! We call this the principle of conservation of mass. It implies that the mass of a closed system must remain constant over time. This principle forms the basis for many equations in fluid mechanics.
So, how do we use this principle in calculations?
Good question! We use the Reynolds transport theorem, which helps relate changes in mass flow through control surfaces. Let's discuss this theorem next.
Reynolds Transport Theorem
Unlock Audio Lesson
The Reynolds transport theorem acts as a bridge between a system's dynamic behavior and its control volume. Can anyone provide details on what control volumes we might encounter?
There's fixed, moving, and deformable control volumes, right?
Correct! A fixed control volume remains constant in space, whereas a moving control volume, like a ship, flows along with the fluid. Lastly, a deformable control volume changes shape over time. Understanding these concepts is crucial for analyzing mass conservation.
Why is it important to distinguish between these types?
Excellent point! Each type of control volume helps us simplify our calculations in different scenarios, leading to accurate mass flow predictions.
Applications of Mass Conservation
Unlock Audio Lesson
Now that we have a firm grasp of the principles, let's discuss practical applications. Can anyone think of a situation where mass conservation is crucial?
Space missions, like when launching satellites!
Absolutely! The Mars Orbiter Mission serves as a perfect example. Successful trajectory calculations rely heavily on understanding the flow of mass in the system, showcasing how pivotal these principles are in practical scenarios.
What happens if we ignore mass conservation in a design?
Ignoring mass conservation could lead to operational failures, like trajectory miscalculations or fluid system malfunctions. That's how essential it is in engineering.
Equations for Mass Conservation
Unlock Audio Lesson
Let's move toward deriving the mass conservation equations. When applying Reynolds transport theorem, we express the change in mass with respect to time. Who remembers what the general form looks like?
It's the integral of density across the control volume and flow across the control surface, right?
Well done! This equation indicates that the mass entering the control volume should equal the mass exiting it, once we account for any changes in stored mass within that volume.
So for steady flow, the mass in equals mass out?
Exactly! That principle is crucial. Remember it—it's integral to solving many fluid mechanics problems.
Wrap-Up and Key Takeaways
Unlock Audio Lesson
To summarize today’s class, we explored the principle of conservation of mass and its applications in fluid mechanics.
And we learned about different control volumes!
Indeed! Keep in mind that recognizing when to apply the mass conservation equation will guide your fluid mechanics studies effectively.
What should we focus on for our next class?
Next, we’ll look into momentum conservation, further applying what we’ve learned today. Great job, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of mass conservation is explored through the Reynolds transport theorem, where the relationship between a system and control volume is established. Different types of control volumes—fixed, moving, and deformable—are described, alongside the implications for calculating mass flow rates in various fluid systems.
Detailed
Conservation of Energy
This section emphasizes the importance of the conservation of mass in fluid mechanics. Mass conservation refers to the principle that mass cannot be created or destroyed in an isolated system, leading to the formulation of key equations based on the Reynolds transport theorem. The distinction between system and control volume is crucial for understanding fluid flows.
Key Points Covered:
- Reynolds Transport Theorem: Establishes the relationship between system and control volume, a fundamental aspect in deriving mass conservation equations.
- Types of Control Volumes:
- Fixed Control Volume: Static in space and time, having defined control surfaces.
- Moving Control Volume: Engaged in fluid systems moving along a trajectory, such as ships.
- Deformable Control Volume: Changes shape over time but remains associated with specific parameters.
- Mass Influx and Outflux: Discusses how mass flows in and out of control volumes, leading to conservation equations.
- Practical applications illustrate how these principles are applied in real-world scenarios like the design of trajectories for space missions. This section wraps up by creating a foundational understanding of mass flow equations, guiding students in problem-solving within fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Conservation Principles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I said earlier, we need to have three equations. One is conservation of mass, the other is momentum, and another is energy. Most of the times you remember whenever you solve the fluid mechanics problems we have three helping hands: it is not two, it is three helping hands. One is conservation of mass, the other is momentum, and another is energy.
Detailed Explanation
In fluid mechanics, understanding the principles of conservation is essential. There are three fundamental conservation equations we must consider: conservation of mass, conservation of momentum, and conservation of energy. These principles act as guiding rules during fluid analysis, ensuring that we account for all changes in a fluid system. Conservation of mass tells us that mass cannot be created or destroyed; it can only flow in or out of a system. Conservation of momentum addresses the forces acting on the fluid and their effects. Finally, conservation of energy considers all forms of energy in the fluid system and how they change over time. All three work together to provide a complete picture of fluid behavior.
Examples & Analogies
Think of a river system. The water flowing through the river represents the mass. As water flows from one area to another, the total amount of water remains the same (conservation of mass). The speed of the water may increase or decrease due to the landscape (conservation of momentum). The kinetic energy of the water when it flows faster is an expression of energy conservation, as it transforms potential energy (like when flowing downhill) into kinetic energy.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
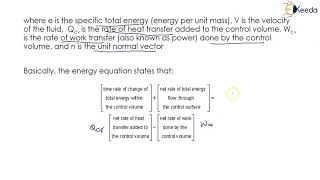
If I put B = m and b = 1, then simplify the problems. D/Dt ∫_CV ρ dV = ∫_CS (ρv · n) dA. This indicates that the net outflow of mass through this control surface is equal to the change of mass storage within the control volume.
Detailed Explanation
To derive the mass conservation equation, we often simplify the parameters by assuming 'B' as mass (m) and 'b' as 1. We then use the integral form, which states that the change in mass within a control volume (CV) over time is equal to the net mass flow across the control surface (CS). The equation shows that any change in mass within a given control volume is proportional to what enters and exits through its surfaces. If the incoming mass is balanced by the outgoing mass, then the mass within that volume remains constant.
Examples & Analogies
A classic example would be a bathtub: when you fill it (mass influx) and the water drains out (mass outflux), the water level changes. Here, the amount of water in the bathtub can be represented as the control volume, and the overflow represents the mass outflux. If you turn off the tap and the drain, the water level stabilizes (no change in mass), demonstrating mass conservation.
Steady Flow Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The net change of the mass in this control volume should be equal to the change of mass storage within the control volume. If the flow is steady, there is no change in the storage within the control volume. What it indicates is that net outflow of this control volume becomes zero.
Detailed Explanation
In fluid dynamics, when we refer to a steady flow, we mean that the flow parameters (like velocity and density) do not change with time at any point within the control volume. Therefore, when we analyze a steady state, the mass coming into the control volume must equal the mass leaving it. This leads to the conclusion that if we sum up the inflows and outflows in a steady-state condition, the total change in the storage of mass will be zero, reinforcing the conservation principle.
Examples & Analogies
Consider a garden hose with a nozzle: when water flows consistently out of the nozzle while you fill the hose, the amount of water in the hose remains the same as long as you don't change the flow from the tap or block the nozzle. This represents steady flow, where inflow equals the outflow.
Equation Simplification in One-Dimensional Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the flow is one-dimensional, instead of doing surface integrals, you can simply sum the inflow and outflow rates, leading to a simplified expression for conservation of mass.
Detailed Explanation
In fluid mechanics, when dealing with one-dimensional flow scenarios—where fluid flows uniformly and straight—the analysis becomes easier. Instead of calculating complex integrals across surfaces to find the total mass flow, we can simply add the mass flow rates at the inlet and outlet. By knowing the density, cross-sectional areas, and velocities, we can derive equations that embody conservation of mass without complex calculations.
Examples & Analogies
Imagine a long tube where water flows in and out from both ends. If you were to determine how much water comes in versus how much goes out, counting the flow rates at each end provides an easier way to see that they balance out, rather than measuring the mass at every point along the pipe.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of Mass: The principle that mass remains constant within a closed system.
-
Reynolds Transport Theorem: A relation that connects the system level behavior of fluids with control volumes.
-
Control Volume Types: The distinction between fixed, moving, and deformable control volumes and their applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The conservation of mass can be illustrated by considering a pipe system where fluid enters and exits. The mass flow rate at the inlet must equal the mass flow rate at the outlet in a steady-state condition.
-
In space missions like the Mars Orbiter Mission, fluid mechanics principles, including mass conservation, played a crucial role in determining the trajectory of spacecraft.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass can’t be created or lost, keep track of it, that’s the cost!
📖 Fascinating Stories
-
Imagine a water tank that fills up from the tap while also draining. If the tap’s flow rate matches the drain’s, the water level stays constant. This illustrates mass conservation in action.
🧠 Other Memory Gems
-
Remember the acronym 'MCC': Mass Conservation Concept for all fluid mechanics studies!
🎯 Super Acronyms
Use 'CVM' to recall
- Control Volume Must always balance mass in and out.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
The principle that mass cannot be created or destroyed in an isolated system across a control volume.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem in fluid mechanics that relates the change in a system to the flow of fluid across its control surface.
-
Term: Control Volume
Definition:
A defined region in space where mass and energy balances are applied to analyze fluid flow.
-
Term: Fixed Control Volume
Definition:
A control volume that does not change its position or orientation in space.
-
Term: Moving Control Volume
Definition:
A control volume that moves with the fluid, analyzed in motion relative to a stationary coordinate system.
-
Term: Deformable Control Volume
Definition:
A control volume whose shape varies with time, allowing for changing flow conditions.