Deformable Control Volume
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore control volumes in fluid mechanics. Can anyone tell me what a control volume is?

Is it a specific volume we analyze to understand fluid flow?

Exactly! We analyze fluid behavior within a defined space. There are three types: fixed, moving, and deformable. Let's discuss them one by one. Who can explain what a fixed control volume is?

It's a control volume that doesn’t change location over time, right?

Correct! And what about moving control volumes?

A moving control volume shifts location while interacting with the fluid, like a ship.

Great! Finally, deformable control volumes change shape over time. Why do you think understanding these is important?

Because it helps in solving real problems where fluid flow isn’t just a straight line.

Exactly! Understanding how mass flows through these volumes helps us derive equations like the conservation of mass.
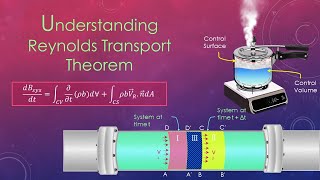
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss how we can use the Reynolds transport theorem for deriving the conservation of mass equation. Who can describe what the theorem states?

It relates the change in a property of a system to the flow of that property across its boundary.

Correct! And when applying this to mass conservation, we find that mass flowing into a control volume must equal the mass flowing out, plus any change in mass inside. Can someone give an example of this in real life?

Like analyzing how much water we have in a tank over time?

Exactly! Let's visualize this: if the flow in equals the flow out, the water level remains constant. That's mass conservation!
Application of Conservation of Mass
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's discuss the applications of the mass conservation equation in engineering. Can anyone think of a scenario where this is critical?

What about missions like the Mars Orbiter, where fluid dynamics are crucial for trajectory?

Great example! The trajectory analysis requires precise calculations of fluid flow and drag forces. How does this tie back to what we learned?

It uses principles like mass conservation to predict how the spacecraft moves through different atmospheres.

Exactly! Fluid mechanics, especially the conservation of mass, is foundational in many advanced fields.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore deformable control volumes, which change shape over time, and their relationship to Reynolds transport theorem for conservation of mass. Various types of control volumes—fixed, moving, and deformable—are discussed, along with real-world applications and the mathematics involved in deriving mass conservation equations.
Detailed
Deformable Control Volume
In fluid mechanics, control volumes are essential in analyzing mass flow. This section discusses deformable control volumes, which can change their shape over time, unlike fixed control volumes, which remain stationary.
Key Types of Control Volumes:
1. Fixed Control Volume: Remains stationary in space.
2. Moving Control Volume: Moves with a particular velocity, like a ship moving through water.
3. Deformable Control Volume: The shape of the volume changes over time, impacting how mass flows through.
Using Reynolds transport theorem, we can derive equations for conservation of mass in these control volumes. The fundamental principle is that mass entering a control volume must equal the mass leaving it, adjusted for any change in mass within the volume itself.
The relevance of this concept is underscored by practical applications, such as the trajectory analysis of spacecraft, which involves careful consideration of drag and fluid dynamics, illustrating the importance of fluid mechanics in engineering and technology.
Youtube Videos





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
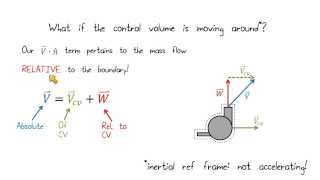
So, that is the strength of the Reynolds transport theorems and, as already I discussed, you can have three type of control volumes, fixed control volume, that means with reference to the space it remains at the same location. As the time goes, it does not move it. That is what fixed control volume is.
Detailed Explanation
In fluid mechanics, understanding control volumes is essential for analyzing how fluids behave in different situations. There are three types of control volumes: fixed, moving, and deformable. A fixed control volume remains stationary in space and does not change location over time. This consistency allows for easier analysis of fluid interactions at that fixed point.
Examples & Analogies
Imagine a bathtub filled with water. As long as the bathtub remains still and the water doesn’t spill out, we can think of the bathtub as a fixed control volume. The water inside can flow in and out through the faucet, but the tub itself stays in one place.
Moving Control Volumes
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The other one is moving control volume, like the ship movement in a sea or the river. The ship and the adjacent fluid can be considered as moving control volume.
Detailed Explanation
A moving control volume is one that changes its position over time. For example, if we picture a ship sailing in the ocean, both the ship and the water around it can be seen as a moving control volume. This means that as the ship travels, it is actively interacting with the water, and both the ship and water conditions affect how fluids flow around it.
Examples & Analogies
Think of a boat gliding through a lake. As the boat moves, it pushes water out of the way, creating waves and ripples. This real-life scenario illustrates how a moving control volume operates: as the boat moves through the water, it impacts the fluid dynamics around it.
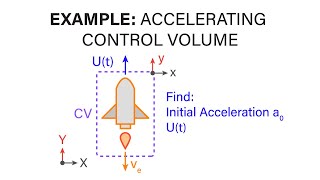
Deformable Control Volumes
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
And we solved many of the problems with moving control volume, considering this control volume is moving with a particular velocity. Not only that, the shape of the control volume can change. That was the deformable control volume.
Detailed Explanation
A deformable control volume is unique because its shape can change over time. This can happen due to variations in fluid flow, pressure, or external forces acting upon it. The ability to analyze deformable control volumes is crucial in understanding complex fluid dynamics where the geometry of the system cannot be fixed.
Examples & Analogies
Consider a balloon being filled with air. As you pump more air into the balloon, its shape changes. The fluid inside (air) pushes the balloon's surface, which stretches and forms a new shape. This example of the balloon represents how deformable control volumes work in a fluid mechanics context.
Comparison of Control Volumes
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, in deformable control volumes, the shape of the control volume changes with time. In case of moving control volume, the control volume moves with a particular velocity. That is what is moving control volume.
Detailed Explanation
To summarize, the main differences among the three types of control volumes lie in their movement and shape. A fixed control volume remains in one position, a moving control volume changes its position but retains its shape, while a deformable control volume not only moves but also changes shape over time. Understanding these distinctions is vital when applying the Reynolds transport theorem for different scenarios in fluid dynamics.
Examples & Analogies
Visualize a roller coaster track, which is a fixed control volume. The trains move along the track (moving control volume). Now, picture a water slide that twists and bends as you go down – that’s akin to a deformable control volume where the path (shape) of the water slide can change as more water flows through it.
Key Concepts
-
Control Volume: A defined space where fluid behavior is observed.
-
Reynolds Transport Theorem: Relates time changes of a fluid's property to its flow across a boundary.
-
Conservation of Mass: Principle stating mass in a closed system stays constant, involving inflow and outflow.
Examples & Applications
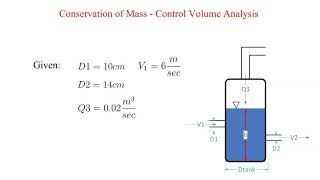
Analyzing water flow in a tank to maintain a steady level.
Studying the trajectory of the Mars Orbiter, where mass flow principles impact navigation calculations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Control volumes in sight, fixed, moving, deformable, tight!
Stories
Imagine a ship sailing through water, its shape influenced by the waves. This represents a moving control volume, while the surrounding sea stays still—a fixed control volume.
Memory Tools
F-M-D: Fixed, Moving, Deformable – the types of control volumes to remember!
Acronyms
CM
Conservation of Mass – always inflow equals outflow!
Flash Cards
Glossary
- Fixed Control Volume
A control volume that remains stationary during the observation period.
- Moving Control Volume
A control volume that moves with a specified velocity with respect to the surrounding fluid.
- Deformable Control Volume
A control volume whose shape changes over time to adapt to fluid flow.
- Reynolds Transport Theorem
A theorem that connects the rate of change of an extensive property within a control volume to the flow of that property across its boundary.
- Conservation of Mass
A principle stating that mass cannot be created or destroyed in a closed system; mass inflow equals mass outflow.
Reference links
Supplementary resources to enhance your learning experience.
