Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
Unlock Audio Lesson
Today, we're going to talk about control volumes. Can anyone remind me what types of control volumes exist?
I think there's the fixed control volume?
Correct! We have fixed, moving, and deformable control volumes. Can someone explain the moving control volume?
It's when the entire control volume moves with the fluid, like a ship sailing in water.
Exactly! And how about deformable control volumes?
They can change shape over time, adapting to the fluid's movement.
Great! Remember, thinking of control volumes helps us analyze fluid dynamics more effectively.
Reynolds Transport Theorem
Unlock Audio Lesson
Now, let's delve into the Reynolds transport theorem. Who can summarize its importance?
It connects system-level equations with control volume equations, especially for mass and momentum.
Exactly! This theorem helps us to establish relationships crucial for deriving the mass conservation equation. Why is mass conservation necessary?
To ensure that mass is neither created nor destroyed in an isolated system!
Right! This principle allows us to simplify many fluid flow problems.
Deriving the Mass Conservation Equation
Unlock Audio Lesson
Let’s derive the conservation of mass equation using RTT. Does anyone remember what the equation involves?
It includes mass inflow and outflow equations across the control surfaces.
Yes! The net mass change in the control volume equals the difference between mass influx and outflux. Can anyone think of a practical example?
Like the flow in pipes connecting to a reservoir.
Exactly! And in steady state, the inflow equals outflow. Remember this balance in real-world problems.
Applications of Mass Conservation
Unlock Audio Lesson
Now, let's talk about applications of mass conservation principles. Can someone give an example?
The Mars Orbiter Mission demonstrated fluid dynamics principles.
Correct! Engineers applied fluid mechanics to design trajectories using mass conservation principles. Why is this significant?
It shows how theoretical knowledge can solve real engineering problems!
Absolutely! Understanding these principles can lead to innovative engineering solutions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the use of Reynolds transport theorem as a foundation for deriving the conservation of mass equation, detailing types of control volumes — fixed, moving, and deformable — and how their motion relative to fluid flow can impact mass flux calculations.
Detailed
Uniformly Moving Control Volume
Overview
In fluid mechanics, it is crucial to understand control volumes and the conservation of mass within those volumes. This section expands upon the Reynolds transport theorem (RTT) to establish the conservation of mass equation applicable to different types of control volumes.
Key Concepts
Control Volumes
There are three main types of control volumes:
1. Fixed Control Volume: Stays in place with reference to a space.
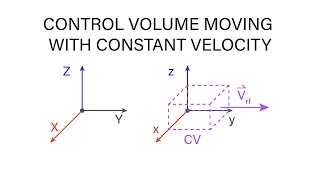
2. Moving Control Volume: Such as a ship on water, where the control volume moves with a velocity relative to the surrounding fluid.
3. Deformable Control Volume: The shape can change over time, adapting to fluid flow conditions.
Reynolds Transport Theorem
The RTT plays a pivotal role, allowing connections between system-level and control volume-level equations, particularly for mass, momentum, and energy.
Mass Conservation
Through applying RTT, the conservation of mass can be derived, indicating that in steady-state and compressible flow, mass influx is equal to outflux in a control volume.
Significance
Understanding these concepts enables the application of fluid mechanics in real-world scenarios such as satellite deployments and other engineering problems. The derivation and application of mass conservation principles are foundational for solving complex fluid flow issues.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Types of Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let’s discuss the three types of control volumes: fixed, moving, and deformable control volumes. A fixed control volume remains stationary despite the passage of time, having definite control surfaces. A moving control volume, such as a ship on water, moves with a certain velocity. Finally, a deformable control volume changes its shape over time.
Detailed Explanation
There are three main types of control volumes: fixed, moving, and deformable. A fixed control volume is stationary, meaning it stays in one place over time with defined boundaries. The moving control volume is dynamic; it moves at a certain speed, making it suitable for analyzing fluid flows around objects, like ships. Deformable control volumes can also move, but additionally, they change shape over time, allowing for different fluid flow scenarios to be modeled. Understanding these types helps in analyzing fluid mechanics problems effectively.
Examples & Analogies
Think of a fixed control volume like a water tank that doesn't move, capturing water flow in and out. A moving control volume is like a boat floating on a river, moving with the current and analyzing how the water interacts with the boat. Lastly, consider a balloon that you inflate and deflate; this represents a deformable control volume where its shape changes as it expands and contracts.
Mass Influx and Outflux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In a control volume, mass influx and outflux are critical for understanding fluid movement. Mass flows into the control volume through the control surface and out of it too. This inflow and outflow can be quantified to derive the conservation of mass equation.
Detailed Explanation
Mass influx refers to the mass that enters a control volume while mass outflux is the mass that exits it. Conservation of mass dictates that the mass accumulating in the control volume must equal the mass coming in minus the mass going out. Therefore, if we visualize this in terms of a water reservoir connected by pipes, the total water entering has to equal the total flowing out for the system to stay in balance.
Examples & Analogies
Imagine a bathtub (our control volume). When you turn on the tap, water is flowing in (mass influx). If you also have a drain open, water is flowing out (mass outflux). For the water level in the bathtub to remain steady (steady state), the amount of water flowing in must equal the amount flowing out.
Understanding Relative Velocity in Moving Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
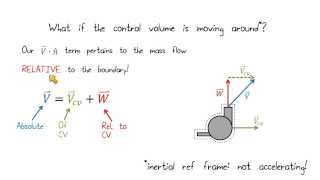
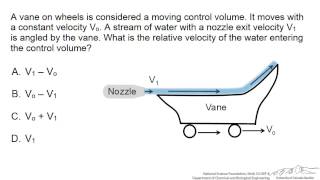
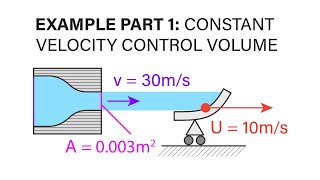
When dealing with moving control volumes, the concept of relative velocity is essential. If a control volume moves with a velocity (Vs) and fluid flows at a different velocity (V), the relative velocity (Vr) will be the difference between these velocities.
Detailed Explanation
In analyzing moving control volumes, like a ship on water, it is important to consider both the speed of the fluid and the speed of the control volume itself. The relative velocity is found by subtracting the speed of the control volume from the fluid’s speed. This relative perspective helps in determining the effective velocity at which fluid approaches or exits the control volume, making it easier to analyze flow interactions.
Examples & Analogies
Consider a person swimming upstream in a river. If the river flows at 5 meters per second and the swimmer swims at 3 meters per second, the relative velocity of the swimmer against the water is 2 meters per second, effectively calculating how fast they are moving forward compared to the ground.
Using Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
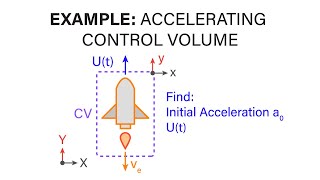
Reynolds Transport Theorem is fundamental in fluid mechanics when dealing with moving control volumes. This theorem relates the change of extensive properties within a control volume to the flow across its control surfaces.
Detailed Explanation
Reynolds Transport Theorem is a powerful mathematical tool in fluid mechanics that connects what happens inside a control volume with what happens at its boundaries. It states that the rate of change of a quantity (like mass) inside the control volume is equal to the net flow of that quantity across the control surface. This theorem helps to translate complex physical situations into manageable mathematical equations, making it a cornerstone in analyzing fluid dynamics.
Examples & Analogies
Think of Reynolds Transport Theorem like keeping track of money in a bank account. The money inside the account represents the control volume. If money flows into the account (influx), that’s like money entering the control volume, and if money flows out (outflux), that’s money leaving the account. The theorem helps you understand how the sum in the account grows or shrinks based on these transactions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volumes
-
There are three main types of control volumes:
-
Fixed Control Volume: Stays in place with reference to a space.
-
Moving Control Volume: Such as a ship on water, where the control volume moves with a velocity relative to the surrounding fluid.
-
Deformable Control Volume: The shape can change over time, adapting to fluid flow conditions.
-
Reynolds Transport Theorem
-
The RTT plays a pivotal role, allowing connections between system-level and control volume-level equations, particularly for mass, momentum, and energy.
-
Mass Conservation
-
Through applying RTT, the conservation of mass can be derived, indicating that in steady-state and compressible flow, mass influx is equal to outflux in a control volume.
-
Significance
-
Understanding these concepts enables the application of fluid mechanics in real-world scenarios such as satellite deployments and other engineering problems. The derivation and application of mass conservation principles are foundational for solving complex fluid flow issues.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship moving through water with a specific velocity acts as a moving control volume.
-
Analyzing fluid flow in pipes connected to a reservoir demonstrates mass conservation in action.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fixed space, volume stands still, moving acts, like a ship on a hill.
📖 Fascinating Stories
-
Once upon a time, a ship traveled steadily over waters, surrounded by a fluid which flowed in and out, demonstrating how mass was conserved.
🧠 Other Memory Gems
-
Remember MCD: Mass Conservation as Dynamics.
🎯 Super Acronyms
VMD
- Volume
- Mass
- Dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A specified region in space where fluid flow is analyzed, distinguished by its boundaries.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem that relates the time rate of change of a system's properties to those of the control volume.
-
Term: Mass Conservation
Definition:
The principle stating that mass cannot be created or destroyed within a closed system; mass influx must equal outflux in steady-state flow.
-
Term: Fixed Control Volume
Definition:
A control volume that does not move with respect to a specified location.
-
Term: Moving Control Volume
Definition:
A control volume that moves with the fluid, such as a ship on water.
-
Term: Deformable Control Volume
Definition:
A control volume whose shape changes over time, adapting to fluid flow conditions.