Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conservation of Mass
Unlock Audio Lesson
Welcome, everyone! Today, we are focusing on the conservation of mass in fluid mechanics. Can anyone tell me what you understand by this principle?
I think it means that mass cannot be created or destroyed, right?
Exactly! It's all about mass continuity. This principle is foundational for solving flow problems. It's important to know that the mass entering a control volume must equal the mass exiting it.
What do you mean by 'control volume'?
A control volume is a defined region in space where we analyze the flow. Remember, we can consider three types of control volumes: fixed, moving, and deformable.
Could you give an example of each?
Sure! A fixed control volume stays in one place, like a tank. A moving control volume could be a ship moving through water, while a deformable control volume would be like a balloon changing shape while it inflates or deflates.
Let's remember this with the acronym 'FMD'—Fixed, Moving, Deformable. Now, why is understanding these concepts important?
It helps us solve fluid dynamics problems effectively!
That's right! And at the end of our discussion, we will employ these concepts to tackle some real-life fluid flow problems.
Types of Control Volumes
Unlock Audio Lesson
Let's dive a bit deeper into our types of control volumes. Who remembers what a fixed control volume is?
It's a region that doesn't move over time, right?
Correct! Now, a moving control volume moves through the fluid? Can anyone give an example of this?
A ship floating on the sea?
Excellent! Now, what about the deformable control volume?
That's when the shape of the control volume can change over time.
Well said! Remember 'FMD' helps us recall: Fixed, Moving, Deformable. It’s crucial to choose the right control volume to solve the problems at hand.
Can someone summarize why we need to differentiate between these types?
It helps in applying the conservation principles accurately to various flow cases!
Exactly, and that leads us nicely into mass conservation equations!
Deriving the Mass Conservation Equation
Unlock Audio Lesson
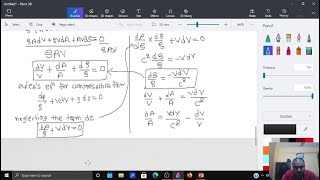
Now, let's focus on deriving the conservation of mass equation. We'll apply Reynolds Transport Theorem.
Can you remind us what that is again?
Of course! It relates how extensive properties change inside a control volume over time. What's our extensive property concerning mass?
It’s mass itself!
Correct! So when we set b=1 for density in our equations, we can simplify our integrals. Does anyone know why density is crucial here?
Because it helps us quantify the mass flow rate entering and exiting the control volume!
Precisely—density links mass with volume flow rate. When we dive into steady and compressible flow, what happens to density?
It varies, but we can handle that if we consider flow to be steady!
Exactly! In steady flow, we can assume density remains constant for simplification. Let's note this as a key point!
Applications and Real-Life Examples
Unlock Audio Lesson
Now, let’s connect our theoretical knowledge with real-life applications. For instance, think about the Mars Orbiter Mission—how does mass conservation apply?
It helps design the trajectory for the spacecraft to ensure it reaches Mars by controlling fuel use and drag forces.
Exactly! By applying fluid mechanics, scientists can predict and adjust trajectories for optimal fuel efficiency.
What other fields use these concepts?
Great question! Besides aerospace, it's vital in civil engineering, especially in designing pipelines and drainage systems.
So, controlling flow and ensuring the right amounts are crucial in those designs?
Yes! It's about balancing inputs and outputs. Remember our previous discussions on 'inflows' and 'outflows' to visualize.
This makes mass conservation so practical and interesting!
Absolutely! It’s a principle that permeates many aspects of engineering and science. Always apply 'FMD' and conservation principles when solving any fluid problem.
Revisiting Key Concepts
Unlock Audio Lesson
Before we conclude today’s session, let’s summarize the key concepts we’ve explored regarding flow conservation.
We learned about control volumes, including what it means to be fixed, moving, or deformable.
We also derived the mass conservation equation using the Reynolds Transport Theorem!
And discussed real-life applications, like the Mars Orbiter Mission!
That's a fantastic recap! Keep the understanding of 'FMD' and conservation principles in mind as they will support your learning throughout this course.
Thanks for the great session! I feel more confident about applying these concepts now.
I’m glad to hear that! Keep practicing, and we will build on this knowledge in our next class.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The conservation of mass is a foundational principle in fluid mechanics. This section elaborates on Reynolds transport theorem, forms of control volumes (fixed, moving, and deformable), and applications involving mass conservation equations in steady and compressible flow scenarios.
Detailed
Steady and Compressible Flow
This section delves into the fundamental aspects of fluid mechanics, particularly focusing on the conservation of mass. Through the lens of Reynolds transport theorem, the relationship between systems and control volumes in fluid dynamics is established. The section discusses three key types of control volumes: fixed control volume, moving control volume, and deformable control volume.
In the context of fluid mechanics, a fixed control volume does not move through space, a moving control volume, like a ship, maintains its location relative to the fluid in motion, and a deformable control volume changes shape over time. Understanding these concepts is crucial for deriving the conservation of mass equation in varying flow conditions.
The principle of conservation of mass holds that the mass influx into the control volume equals the mass outflux. The section explains how this principle can be applied in steady flow cases, illustrating the simplification when the density remains constant. It sets the stage for discussing real-life applications such as the Mars Orbiter Mission, showcasing the relevance of fluid mechanics in advanced aerospace scenarios.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Steady Compressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
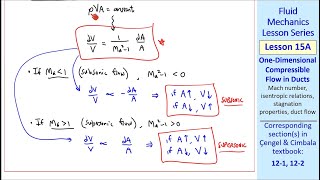
In steady and compressible flow, the density of the fluid can change but remains constant over time at any given point. This means that, while different parts of the fluid may have different densities, if you observe a specific point in the flow, the density there does not vary with time.
Detailed Explanation
In fluid mechanics, a flow is considered steady if its properties (like velocity, pressure, and density) do not change with time at any particular location. In the case of compressible flow, the density is allowed to vary throughout the fluid. For instance, when air moves at high speeds, its density changes due to variations in pressure and temperature. If we analyze a specific point in this flow, we find that while density might change at different locations in the flow field, it remains constant if we look at it at the same place over a period of time.
Examples & Analogies
Imagine a balloon being slowly deflated. At any given point in the balloon that you measure, the density of the air remains constant over time, even though the overall density of the balloon's content may change as air escapes.
Simplification of Flow Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When dealing with steady incompressible flow, the density can be treated as constant, allowing for significant simplifications. This leads to easier calculations focusing on surface integrations rather than complex volume integrals.
Detailed Explanation
In many practical problems where the density of the fluid does not change significantly, we can consider the flow to be incompressible. This means the density is constant and can be factored out of the equations, reducing the complexity significantly. Instead of performing complicated integrals over the entire control volume, we can apply surface integrals on the control surface only, making the calculations much simpler. For engineers and scientists, this simplification is essential in designing systems that involve fluids, as it reduces calculation time and potential errors.
Examples & Analogies
Think of a thick smoothie in a blender. As the ingredients blend, their density doesn't change much, allowing you to calculate how much will flow out of the spout simply by measuring the outline of the container rather than looking at the mixture in full.
Control Volumes and Their Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
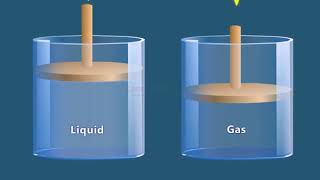
In fluid mechanics, we often utilize three types of control volumes: fixed, moving, and deformable. A fixed control volume remains in the same position in space, whereas a moving control volume, like a ship, travels through the fluid. A deformable control volume changes shape over time.
Detailed Explanation
Control volumes are essential tools in fluid mechanics that allow for the analysis of fluid flow. A fixed control volume does not move and thus simplifies our calculations because its boundary conditions stay the same over time. A moving control volume, however, travels with the fluid, such as a boat on water, requiring a consideration of relative velocities between the fluid and the boat. Lastly, a deformable control volume changes shape, which means that the fluid's flow characteristics must be constantly reevaluated, adding complexity to the analysis.
Examples & Analogies
Imagine a water tank that is stationary (fixed control volume), a water bottle being carried by someone while they walk (moving control volume), and a balloon being squeezed and expanded (deformable control volume). Each scenario requires different considerations for the effects of fluid behavior.
Relative Velocity in Moving Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When analyzing flows in moving control volumes, we must consider relative velocities. If a control volume moves at velocity V_s while the fluid has a velocity V, we calculate the relative velocity to properly describe the flow dynamics at the control surface.
Detailed Explanation
In a moving control volume, it is crucial to calculate the fluid's velocity relative to the control volume's velocity. This means that if the fluid flows in the same direction as the control volume, their velocities subtract to yield a positive relative velocity. Conversely, if the fluid moves opposite to the control volume, this creates a negative relative velocity. Understanding relative velocity helps us analyze fluid interactions more accurately, especially when studying things like vehicles moving through a fluid.
Examples & Analogies
Think of a swimmer in a river. If the river flows at 2 m/s downstream and the swimmer swims at 3 m/s upstream, the swimmer's relative velocity is 1 m/s upstream. This relative motion affects how far the swimmer can travel upstream against the flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined region in space for fluid flow analysis.
-
Reynolds Transport Theorem: Important for determining changes within a control volume.
-
Conservation of Mass: Mass in a closed system remains constant over time.
-
Steady Flow: A condition where fluid properties at any point are constant with time.
-
Compressible Flow: Flow where density variations are significant and affect the dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A pipe system where water enters at one end and exits at the other, demonstrating steady flow.
-
The trajectory of a satellite like the Mars Orbiter Mission can be modeled using the principles of fluid dynamics and conservation of mass.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flow we find with glee, mass is conserved, constantly!
📖 Fascinating Stories
-
Consider a ship sailing smoothly across the sea—its mass remains the same, influenced by the rhythmic waves of the fluid. Just like in fluid dynamics, where the principle of mass balance keeps everything steady.
🧠 Other Memory Gems
-
Remember 'FMD'—Fixed, Moving, Deformable control volumes!
🎯 Super Acronyms
Use 'MFS' for Mass Flow Stability
- Mass
- Flow
- Steady!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space through which fluid can flow, used in analyzing fluid dynamics.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change in a system to the flow of fluid through a control volume.
-
Term: Conservation of Mass
Definition:
A principle stating that mass cannot be created or destroyed in an isolated system.
-
Term: Steady Flow
Definition:
A flow condition where fluid properties at a point do not change over time.
-
Term: Compressible Flow
Definition:
Flow in which the fluid density changes significantly within the flow field.