Reynolds Transport Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will talk about control volumes and their role in fluid mechanics. Can anyone tell me what a control volume is?

Isn't it a designated space through which fluid flows?

Exactly! Control volumes can be fixed, moving, or deformable. Remember, in a fixed control volume, boundaries don't move, while in a moving control volume, like a ship, they do. Can anyone think of a practical example?

A car moving through air might be an example of a moving control volume?

Great point! Now, when we analyze problems in fluid dynamics, we often need to establish the flow characteristics through these control volumes. Does anyone remember why it's important?

It helps us understand mass conservation during fluid flow.

Exactly—a principle we derive from the Reynolds Transport Theorem!
Mass Conservation Fundamentals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s delve into the mass conservation equation. Can anyone explain what it signifies in fluid mechanics?

That the mass entering a control volume equals the mass leaving it, right?

Yes! It can be expressed as a mathematical equation. If we have a control volume, the mass influx should equal the mass outflux plus any change in mass storage. Can we express that mathematically?

It might look like: inflow - outflow = d(mass storage)/dt?

Perfect! And when we simplify this for steady flow, what happens?

The mass storage term becomes zero, so net mass inflow equals net mass outflow.

Exactly! That understanding is crucial for solving fluid dynamics problems.
Real-life Applications of Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

How do you think the principles we’ve discussed relate to real-world scenarios?

Like engineering projects, for instance, designing bridges or buildings?

Yes! And let's consider the Mars Orbiter Mission—how fluid mechanics principles were applied to design the trajectory. Does anyone know why fluid dynamics is significant in this context?

Because when launching a satellite, you need to account for drag forces and mass flow to successfully reach orbit!

Exactly! Fluid mechanics helps us model not just terrestrial systems but also space travel. Really versatile!
Mathematical Formulations in Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's look at mathematical applications. How do we calculate mass flow rates using integrals?

Is it about integrating velocity times density over the control surface?

Exactly! The equation involves surface integrals of velocity components and density. How would we apply this in a real case?

Let’s say we have a pipe, we need the area, velocity, and density to compute mass flux.

Right! And if we have varying flow conditions, we might need numerical methods or computational tools. Does anyone have experience with MATLAB or similar software in this regard?

I’ve used MATLAB for simulations! It simplifies calculating complex integrals.

Exactly! We will transcend the basics and leverage technology to tackle complex scenarios.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section delves into the Reynolds Transport Theorem, explaining the distinction between systems and control volumes in fluid mechanics, the derivation of mass conservation equations, and the importance in solving complex fluid flow problems across various scenarios involving fixed, moving, and deformable control volumes.
Detailed
Detailed Summary of the Reynolds Transport Theorem
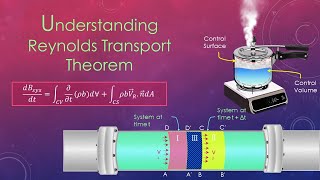
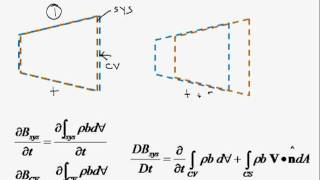
The Reynolds Transport Theorem is a fundamental principle in fluid mechanics used to establish a link between the behavior of a system (the physical fluid mass under consideration) and that of a control volume (a defined region in space through which fluid flows). In this section, we outline:
- Concept of Control Volumes: The distinction between fixed, moving, and deformable control volumes is critical. A fixed control volume is stationary, whereas a moving control volume follows the fluid flow, such as a ship in water. Deformable control volumes can change shape over time, which is relevant in certain fluid dynamics scenarios.
- Conservation of Mass: The mass conservation equation derived from the Reynolds Transport Theorem is pivotal in analyzing fluid flow. It demonstrates that the rate of mass entering and exiting a control volume must equal any mass accumulation, leading to insights on mass flux within a system.
- Applications of Fluid Mechanics: Real-world applications such as the trajectory design for satellites, specifically for the Mars Orbiter Mission, illustrate how advanced fluid mechanics concepts are utilized to achieve precise and complex objectives.
- Mathematical Approaches: The section includes mathematical formulations involving differential and integral calculus to compute mass flow rates. Surface integrals and volume integrals help quantify mass flow across control surfaces, emphasizing the ease of calculations under steady and incompressible flow conditions.
This theorem serves as a corner piece in many fluid mechanics applications, facilitating fluid flow analysis across various disciplines.
Youtube Videos


![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
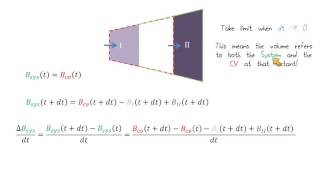
If you remember, I discussed very thoroughly what is the difference between systems and the control volume. Mostly in fluid mechanics, we follow the control volume aspect. That is the reason we need a relationship between the system and the control volume. The Reynolds transport theorems establish the relationship of conversions of mass from system to control volume.
Detailed Explanation
This chunk introduces the basic concepts of 'systems' and 'control volumes' in fluid mechanics. A 'system' typically refers to a specific quantity of fluid under consideration, while a 'control volume' is a defined region in space through which fluid can flow. The Reynolds transport theorem provides a mathematical framework to relate these two concepts, allowing us to analyze the mass flow from a system to a control volume effectively.
Examples & Analogies
Think of a control volume like a fish tank. The tank represents the control volume where you can measure the water's movement in and out, akin to mass flow. The specific amount of water in the tank at any time is your 'system.' Just as you might observe how water flows in and out of the tank, the Reynolds transport theorem helps us quantify and analyze fluid movements in larger systems.
Types of Control Volumes
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
As already I discussed, you can have three types of control volumes: fixed control volume, moving control volume, and deformable control volume.
Detailed Explanation
This chunk describes the three different types of control volumes that can be used in fluid mechanics. A fixed control volume remains stationary in space and does not change its shape. A moving control volume moves with a fluid (like a ship in water), taking the fluid with it. The deformable control volume can change its shape or size over time. Understanding these types is crucial for selecting the right approach to apply the Reynolds transport theorem in practical scenarios.
Examples & Analogies
Imagine a balloon filled with air. While it's stationary, it represents a fixed control volume. If you were to move the balloon through the air, it would then be a moving control volume. If you squeeze the balloon, changing its shape while filled, that could illustrate a deformable control volume. Each scenario helps highlight how fluid mechanics can adapt to different situations.
Mass Conservation in Fluid Flow
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
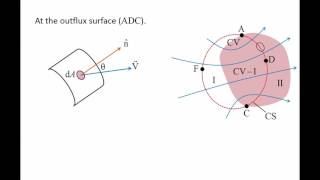
As I said earlier, when you have the control volume, through the control surface there is mass influx coming into the control volume, going out from the control volume.
Detailed Explanation
This chunk emphasizes mass conservation within a control volume. It states that when analyzing fluid flow, one must account for both the mass entering and exiting the control volume. The mass influx and outflux are essential for applying the principle of conservation of mass, helping us understand how fluid behaves over time within the designated volume.
Examples & Analogies
Consider a bathtub filling with water. The water entering the bathtub represents the mass influx, while the water that drains out when you release the plug represents the outflux. For a bathtub to stay at the same water level (steady state), the amount of water flowing in must equal the amount flowing out—illustrating the conservation of mass.
Simplifying Mass Conservation Analysis
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We made it one-dimensional flow problem. If you have the same steady flow mass conservation mass level or this one, the same concept, only here we are putting it.
Detailed Explanation
This chunk discusses how mass conservation analyses can be simplified by focusing on one-dimensional flow. In many real-world applications, fluid flow can be approximated to one dimension, making the calculations of mass inflow and outflow easier. This simplification allows engineers to evaluate fluid flows without handling complex three-dimensional variables.
Examples & Analogies
Think about water flowing through a straight garden hose. You have a clear inlet where water comes in and an outlet where the water flows out. You can easily measure how much water flows through in a simple linear fashion, akin to one-dimensional flow. By keeping it simple, calculations become straightforward, helping you manage the water flow more effectively.
Using Reynolds Transport Theorem
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you consider the control volume moving with a certain velocity, we use the relative velocity things...
Detailed Explanation
This chunk explains how the Reynolds transport theorem is adjusted when dealing with moving control volumes. The concept of relative velocity becomes important as we analyze the fluid moving through a control volume that is itself also in motion. This establishes a new perspective on how fluid and control volume velocities interact, allowing us to accurately predict mass flow dynamics.
Examples & Analogies
Imagine riding in a boat moving upstream on a river. The speed of the water (fluid velocity) around you is one factor, but because your boat is also moving, you experience a different flow relative to the bank of the river. Understanding these relative velocities is similar to utilizing the Reynolds transport theorem for a moving control volume, where both the river current and boat speed need to be accounted for.
Key Concepts
-
Control Volume: A region in fluid flow used to analyze mass and energy transfer.
-
Reynolds Transport Theorem: Establishes a connection between system and control volume behaviors.
-
Mass Conservation: Essential principle maintaining mass balance in fluid dynamics.
Examples & Applications
Designing a water transport system for a city, ensuring mass inflow equals outflow at junctions.
Calculating the trajectory of the Mars Orbiter by analyzing fluid forces acting during launch.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When the volume is set, watch the mass flow net. What goes in must flow out, that's what it's about!
Stories
Imagine a city with a reservoir where water flows in and out through pipes. A flood means too much flows in, but the engineers ensure it balances perfectly—this teaches about mass conservation.
Memory Tools
Control Volumes Maintain Mass: C-M-M.
Acronyms
R.T.T. for 'Reynolds Transport Theorem' - Remember Transport for 'Flow'.
Flash Cards
Glossary
- Control Volume
A specified region in space through which fluid flows, used for analyzing fluid mechanics.
- Reynolds Transport Theorem
A fundamental theorem that relates the rate of change of a property within a control volume to the influx and outflux through its surface.
- Mass Conservation
The principle that mass cannot be created or destroyed within a control volume, leading to a balance between inflows and outflows.
- Steady Flow
A flow condition where fluid properties at any point remain constant over time.
- Incompressible Flow
A flow where the fluid density remains constant.
- Surface Integral
A mathematical operation used to compute flux across a surface within the control volume.
- Vector Field
A representation of a quantity that has both direction and magnitude at every point in space.
Reference links
Supplementary resources to enhance your learning experience.
