Acceleration Field
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll explore the concept of acceleration in fluids. Can anyone tell me how we define acceleration?

Isn't it the change in velocity over time?

Exactly! Acceleration is indeed defined as the time derivative of velocity. This is crucial when we analyze fluid motion because it helps us understand how fluid particles behave.

How does that relate to Newton's second law?

Great question! Newton's second law states that force equals mass times acceleration. Both force and acceleration are vector quantities, meaning they have both magnitude and direction.

What does that mean for fluid particles?

It means we can apply these principles at the particle level when analyzing fluids!

Let’s summarize: Acceleration is defined as the change in velocity over time, and it's related to force through Newton's second law.
Local and Convective Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've defined acceleration, let’s differentiate between local and convective acceleration. Who can explain what local acceleration means?

I think local acceleration is how velocity changes at a specific point over time?

Exactly, local acceleration looks at a single point in space. Now, what about convective acceleration?

Isn't it related to how particles move in relation to one another across different points?

Yes! Convective acceleration arises due to varying velocities of fluid particles as they move through space. Both concepts combined provide a full picture of acceleration in a fluid.

To remember these, think: Local = Point; Convective = Movement. Local acceleration depends on time, while convective relies on spatial changes.

To summarize, local acceleration measures changes over time at one spot, while convective acceleration measures changes across different points. Both are crucial for understanding dynamics.
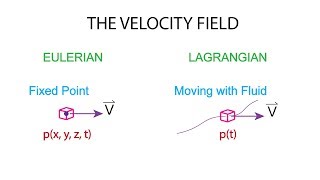
Velocity and Acceleration Relationship
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s connect acceleration back to velocity fields mathematically. Who remembers what the del operator is?

Isn't it the gradient operator?

Correct! The del operator helps us find how velocity changes in space, which allows us to compute the acceleration using partial derivatives.

Why are those derivatives important?

They are key for expressing acceleration as a function of velocity in different directions. Understanding how this works helps us analyze fluid motions more effectively.

Summarizing, the del operator shows us the spatial variations of velocity, and we use these to derive acceleration components effectively.
Material Derivatives in Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s shift to the concept of material derivatives. Can anyone recall what a material derivative does?

Is it the total change experienced by a fluid particle, including time and space?

Exactly! The material derivative combines both local and convective accelerations to tell us how a particle's properties evolve.

How would we use this in practice?

We calculate things like changes in pressure and temperature in fluid motion. It's essential for predicting how fluids behave.

So to wrap up, material derivatives provide a comprehensive view of how a fluid particle's properties change over time as it moves through space.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we delve into how acceleration is defined in both Lagrangian and Eulerian frameworks, and how it relates to fluid dynamics. We cover how the velocity of fluid particles affects acceleration, the importance of local and convective accelerations, and the mathematical representation of these components. Practical examples and exercises illustrate these concepts.
Detailed
Detailed Summary of Acceleration Field
In this section, we analyze the acceleration of fluid particles, which is fundamentally the time derivative of particle velocity. Under Newton's second law, force is defined as the mass of an object multiplied by its acceleration, highlighting their vector nature. Thus, we utilize the concepts of local and convective acceleration in both Lagrangian and Eulerian frameworks to explore how these components impact fluid motion.
Key Points Covered:
- Acceleration as a Derivative: The acceleration of a fluid particle can be expressed as the time derivative of its velocity, which complicates calculations when considering position and time variables from a multivariable calculus perspective.
- Taylor Series Application: The expansion of variables using the Taylor Series demonstrates how to relate different components of acceleration to spatial coordinates and time.
- Local vs. Convective Acceleration: Local acceleration refers to how velocity changes at a specific point over time, while convective (or advective) acceleration results from velocity changes across different spatial positions, emphasizing the need to consider both when analyzing fluid dynamics.
- Mathematical Modeling: The del operator (gradient operator) is integral to formulating the acceleration vector field and relates changes in velocity to acceleration effectively.
- Material Derivative: This concept helps us account for variations of quantities like velocity, density, and pressure with respect to both time and space.
Through practical examples and extensive mathematical representation, the section illustrates how to compute acceleration fields using velocity field data, summing up the main concepts necessary for understanding fluid dynamics.
Youtube Videos
![Components of Acceleration Field [Fluid Mechanics #14]](https://img.youtube.com/vi/G_mG5ALxFrY/mqdefault.jpg)
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Newton's Second Law and Force
Chapter 1 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, similar way if I am looking at Newton's second law also see that force is equal to mass into acceleration, force is vector component, acceleration is the vector component, okay and both are the parallels okay, so force and the vector, at the particle levels like in solid mechanics, the force we can put is mass into acceleration.
Detailed Explanation
Newton's Second Law states that the force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma). In fluid dynamics, we can apply this principle to particles in a fluid. Here, both force and acceleration are treated as vector quantities, meaning they have both magnitude and direction. This relationship is essential for analyzing the motion of particles within the fluid.
Examples & Analogies
Think of a soccer ball. If you kick it (apply a force), the speed with which it accelerates depends on how hard you kicked it (the force) and how heavy it is (the mass). If a child kicks the ball lightly, it will not accelerate much, but if an adult kicks it with force, it will accelerate significantly. This analogy helps illustrate how force, mass, and acceleration interact.
Particle Acceleration Calculation
Chapter 2 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let us look it at the particle levels, if I had to find out what is the acceleration of the fluid particles? Is nothing else is a time derivative of velocity of the particles, as you know it from class 10, 11th and 12th I am just doing this time derivative of the velocity; particle velocities with respect to time and that is what represents the accelerations, at the particles levels you will have these.
Detailed Explanation
To understand the acceleration of fluid particles, we need to calculate how their velocity changes over time, known as the time derivative of velocity. This means observing how fast the velocity of a particle changes can tell us how it is accelerating. In equations, we write acceleration (a) as the change in velocity (Δv) divided by the change in time (Δt). This basic principle is a key concept in mechanics.
Examples & Analogies
Imagine a car speeding up. The driver's foot on the accelerator pedal makes the car go faster over time. If the car goes from 20 km/h to 60 km/h in 4 seconds, its acceleration can be calculated by how much its speed changed divided by the time taken. Similarly, fluid particles speed up or slow down as conditions change, like the car responding to the driver's actions.
Understanding Velocity and Position Variability
Chapter 3 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if you look at this the velocities has a variability in positions and the time because of that though when you define a; derivative with respect to time you will have a local component okay, you will have a with a x particle directions, y particle directions and z particle direction.
Detailed Explanation
Velocity does not remain constant in a fluid; it varies based on both time and position. This variability means that when we calculate the derivative (the rate of change) of velocity concerning time to find acceleration, we must take into account that different particles may be moving in different directions, such as x, y, and z axes. Each direction will affect their acceleration differently, introducing local components in our calculations.
Examples & Analogies
Envision a river with varying flow. In some parts, the water flows quickly, while in others, it flows slowly. If you were to throw leaves into the river, each leaf would accelerate at different rates and directions based on where it is located in the flow. That's how particles in a fluid behave as they experience different velocities at various positions.
Taylor Series and Particle Motion
Chapter 4 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is nothing else if you are considering is a 2 variables like I just discussed you the Taylor series, if you remember it defining for the 2 variables in this case, I have a Taylor series of 4 variables the x, y, z and the t. If you expand it and take it only these 4 terms, you will get this component nothing else, we are near to the same Taylor series concept what we discussed in a single variables.
Detailed Explanation
The Taylor series is a mathematical tool that helps us expand functions into polynomials, which can be very useful when dealing with complex variables, like those we encounter in fluid mechanics (x, y, z positions and time t). When applied to our understanding of acceleration and velocity in fluid particles, it allows us to approximate and analyze the behavior of particles based on their positions and the time at which we observe them.
Examples & Analogies
Consider a musician tuning a piano. Each note can vary based on small adjustments, and the musician can use a series of adjustments (similar to Taylor series) to achieve the perfect pitch. In fluid mechanics, just like tuning, we adjust the calculations of particle behavior by accounting for their changing positions and speeds over time.
Components of Acceleration
Chapter 5 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, if I put it that I will get it the accelerations fields as I explaining it that, I will have a particle, the change of the position the particles in the x direction with respect to time will give you the velocity component in that directions, so this is for x component, so y component, z component, so the finally this accelerations will have this form, accelerations will have this form.
Detailed Explanation
The overall acceleration of a particle in a fluid can be broken down into components. Each component corresponds to a specific directional change—x, y, or z. By studying how the positions change over time and how this affects velocity in each of these directions, we gain a full picture of how the particle is accelerating within the fluid.
Examples & Analogies
Think of a drone flying through the air. Its acceleration can be different as it moves up (z-direction), side to side (x-direction), or forward and backward (y-direction). By considering each movement direction, we understand how fast and in what way the drone is speeding up or slowing down, similar to how we analyze particles in fluid.
Local and Convective Acceleration
Chapter 6 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at that this is what is called the local accelerations, the velocity changes as with respect to the time only, so that means at the probe equations because of only the velocity changes at that locations will give us the local accelerations. Velocity is also changes because of change of the velocity field that is the velocity variances x gradient, y gradient, z gradient and the u, v, w component.
Detailed Explanation
In fluid dynamics, we define local acceleration as the change in velocity of a particle at a specific point over time. Conversely, convective acceleration refers to changes in velocity due to the particle's movement through a velocity field where the speed or direction may change based on its position. Thus, local acceleration deals with how fast a particle’s speed is changing at a point, while convective acceleration accounts for the broader context of the particle moving through a varying flow.
Examples & Analogies
Imagine driving a car on a highway with varying speed limits. If you're in one spot, you might be going 60 km/h (local acceleration). But if you then enter a zone where the speed limit is lower (convective acceleration), you will either slow down or see another car zoom past you. Thus, local effects vs. those caused by the environment around you matter greatly in fluid dynamics as they do in everyday driving.
The Gradient Operator and Derivatives
Chapter 7 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at these same acceleration fields, if I looking it as a delta operators or the gradient operator, you will know it we can define it as i, j functions like this and the accelerations component; the scalar component of accelerations in the x direction, y and z direction can have it like this.
Detailed Explanation
The gradient operator, often denoted as 'del' (∇), is crucial in mathematics and physics for indicating how a quantity changes in space. In the context of acceleration fields, using this operator allows us to define each acceleration component more clearly in various spatial directions (x, y, and z). By doing this, we can more precisely understand how different factors in a fluid influence particle motion.
Examples & Analogies
Imagine you're using a GPS app that shows you the steepness of different hills in an area. The GPS uses gradients to indicate how steep roads are based on changes in elevation. Similarly, the gradient operator helps us understand how steep gradients in fluid motion change particle accelerations in specific directions.
Material Derivative Concept
Chapter 8 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
But many of the times people talk about material derivative, it is nothing else, it is that the change it is a special name of material derivative means, when you talk about a particles along the particles, you compute the derivative with respect to time is a total derivative or the material derivative or the particle derivatives is nothing else.
Detailed Explanation
The material derivative is an important concept in fluid mechanics that describes how a particle's properties change as it moves through the fluid. It captures both the changes caused by local effects and those due to the motion of the particle itself, referring to this combined effect as a total derivative. Essentially, it tells us how something changes as it moves along its path.
Examples & Analogies
Consider a surfer riding a wave. As they move along the wave, their speed and direction may change due to the wave’s shape and action. The material derivative accounts for this by describing how the surfer's experience changes based on both their movement through the water and the water's flow itself.
Conclusion of Acceleration Fields
Chapter 9 of 9
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, as this fluid having this velocity field, we can compute the accelerations field, we can compute this material derivative of the pressures, we can compute the material derivative of density with the same format, we can compute and we can solve the problems in this way.
Detailed Explanation
In summary, understanding velocity fields and how they relate to acceleration helps us compute critical parameters in fluid dynamics, including material derivatives of pressure and density. This knowledge enables us to analyze the behavior of fluids effectively, thus applying mathematical techniques to solve fluid dynamics problems.
Examples & Analogies
Imagine a chef experimenting with a new recipe while cooking. By understanding how flavors blend over time, the chef can modify ingredients (like pressure and density in a fluid) to achieve the desired taste. Similarly, we can manipulate velocity fields in fluid dynamics to achieve intended outcomes in various engineering applications.
Key Concepts
-
Acceleration: The rate of change of velocity with respect to time.
-
Local Acceleration: Change in velocity occurring at a specific point in time.
-
Convective Acceleration: Change in velocity experienced by fluid particles across different spatial locations.
-
Material Derivative: Combines local and convective changes to express the total change experienced by a particle.
-
Del Operator: A mathematical operator used to determine gradients and changes in flowing fluids.
Examples & Applications
Example of local acceleration: An increase in velocity observed at a fixed point in a flowing river as water moves past.
Example of convective acceleration: Water particles flowing around a bend in a river will experience different velocities based on their position in the flow.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Acceleration, swift and fast, / Change over time, forever will last.
Stories
Imagine two boats in a flowing river. One stays still, while the other moves swiftly around bends. The one that stays still experiences local acceleration, while the one that moves experiences convective changes.
Memory Tools
Remember 'L' for Local, 'C' for Convective. Local changes at a point, Convective moves with the current.
Acronyms
A.C.M. stands for Acceleration, Convective acceleration, Material derivative.
Flash Cards
Glossary
- Acceleration
The rate of change of velocity with respect to time.
- Local Acceleration
The change in velocity at a specific point over time.
- Convective Acceleration
The change in velocity of a fluid particle as it moves through different points in space.
- Material Derivative
An operator that expresses the total derivative of a property of a moving fluid particle, accounting for both time and space variations.
- Del Operator
A vector differential operator that represents gradients, divergences, and curls in vector fields.
Reference links
Supplementary resources to enhance your learning experience.
